Fr Free variables Variables used but not bound within - PowerPoint PPT Presentation

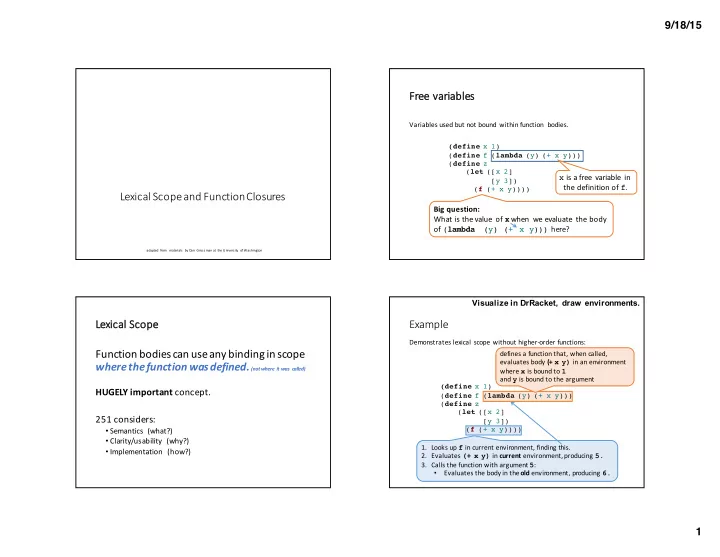
9/18/15 Fr Free ¡ ¡variables Variables ¡used ¡but ¡not ¡bound ¡within ¡function ¡ bodies. (define x 1) ( define f ( lambda (y) (+ x y))) ( define z ( let ([x 2] x is ¡a ¡free ¡ variable ¡ in ¡ [y 3]) the ¡definition ¡of ¡ f . ( f (+ x y)))) Lexical ¡Scope ¡and ¡Function ¡Closures Big ¡question: What ¡is ¡the ¡value ¡ of ¡ x when ¡ we ¡evaluate ¡ the ¡body ¡ of ¡ ( lambda (y) (+ x y))) here? adapted ¡ from ¡ materials ¡ by ¡Dan ¡ Grossman ¡at ¡ the ¡University ¡ of ¡Washington Visualize ¡in ¡DrRacket, ¡ draw ¡ environments. Lexical ¡ Le ¡Scope Example Demonstrates ¡lexical ¡scope ¡without ¡higher-­‑order ¡functions: Function ¡bodies ¡can ¡use ¡any ¡binding ¡in ¡scope ¡ defines ¡a ¡function ¡that, ¡when ¡called, ¡ evaluates ¡body ¡ (+ ¡ x y) in ¡an ¡environment ¡ where ¡the ¡function ¡was ¡defined. ¡ (not ¡where ¡it ¡was ¡ called) where ¡ x is ¡bound ¡to ¡ 1 and ¡ y is ¡bound ¡to ¡the ¡argument (define x 1) HUGELY ¡important concept. ( define f ( lambda (y) (+ x y))) ( define z ( let ([x 2] 251 ¡considers: [y 3]) • Semantics ¡ (what?) ( f (+ x y)))) • Clarity/usability ¡ (why?) 1. Looks ¡up ¡ f in ¡current ¡environment, ¡finding ¡this. • Implementation ¡ (how?) 2. Evaluates ¡ (+ y) in ¡ current environment, ¡producing ¡ 5. x 3. Calls ¡the ¡function ¡with ¡argument ¡ 5 : • Evaluates ¡the ¡body ¡in ¡the ¡ old environment, ¡producing ¡ 6. 1

9/18/15 Cl Closures Example re revising ¡ ¡ our ¡ r ¡definition ¡ ¡ of ¡ ¡functions Demonstrates ¡lexical ¡scope ¡without ¡higher-­‑order ¡functions: A ¡ function ¡definition ¡expression evaluates ¡to Creates ¡a ¡closure ¡and ¡binds ¡ f to ¡it: a ¡ function ¡closure value. Code: ¡ ( lambda (y) (+ x y)) Environment: ¡ f à this ¡closure, ¡ x à 1 à Not ¡a ¡cons ¡cell. (define x 1) A ¡ function ¡closure has two ¡parts: Cannot ¡access ¡pieces. ( define f ( lambda (y) (+ x y))) • code of ¡function ( define z ( let ([x 2] • environment where ¡the ¡function ¡was ¡defined [y 3]) ( f (+ x y)))) A ¡ function ¡call ¡expression: 1. Looks ¡up ¡ f in ¡current ¡environment, ¡finding ¡this ¡closure. • Evaluates ¡the ¡code ¡of ¡a ¡function ¡closure 2. Evaluates ¡ (+ y) in ¡ current environment, ¡producing ¡ 5. x 3. Evaluates ¡the ¡closure’s ¡function ¡body ¡ (+ y) in ¡the ¡closure’s ¡ x • In ¡the ¡environment ¡of ¡the ¡function ¡closure environment ¡( f à the ¡closure, ¡ x à 1 ), ¡extended ¡with ¡ y à 5 , ¡ à producing ¡ 6. Ex: ¡Returning ¡a ¡function env pointer shows ¡ env structure, ¡ by ¡pointing ¡ to “rest ¡of ¡environment” The ¡ Th ¡Rule: ¡ ¡Lexical ¡ ¡Scope binding maps ¡variable ¡name ¡to ¡value A ¡function ¡body ¡is ¡evaluated ¡in ¡the ¡environment ¡ (define x 1) x 1 where ¡the ¡function ¡was ¡defined (created), ¡ extended ¡with ¡bindings ¡for ¡the ¡arguments. (define (f y) (let ([x (+ y 1)]) Next: (lambda (z) • Even ¡taking ¡/ ¡returning ¡ functions ¡with ¡higher-­‑order ¡ (+ x y z))) functions! (define z (let ([x 3] • Makes ¡first-­‑class ¡functions ¡much ¡more ¡powerful. [g (f 4)] • Even ¡if ¡counterintuitive ¡at ¡first. [y 5]) • Why ¡alternative ¡ is ¡problematic. (g 6) )) More ¡examples ¡in ¡closures.rkt, ¡notes. ¡ ¡Draw… 2

9/18/15 Ex: ¡Returning ¡a ¡function Ex: ¡Returning ¡a ¡function env pointer env pointer shows ¡ env structure, ¡ by ¡pointing ¡ to shows ¡ env structure, ¡ by ¡pointing ¡ to “rest ¡of ¡environment” “rest ¡of ¡environment” binding binding maps ¡variable ¡name ¡to ¡value maps ¡variable ¡name ¡to ¡value (define x 1) (define x 1) x 1 x 1 (define (f y) (lambda (y) (define (f y) (lambda (y) f f env (let ([x (+ y 1)]) env (let ([x (+ y 1)]) (lambda (z) (lambda (z) (let ([x (+ y 1)]) (let ([x (+ y 1)]) (+ x y z)) (+ x y z)) (lambda (z) (lambda (z) (+ x y z))) (+ x y z))) x 3 (define z (let ([x 3] (define z (let ([x 3] [g (f 4)] [g (f 4)] [y 5]) [y 5]) (g 6) )) (g 6) )) Ex: ¡Returning ¡a ¡function Ex: ¡Returning ¡a ¡function env pointer env pointer shows ¡ env structure, ¡ by ¡pointing ¡ to shows ¡ env structure, ¡ by ¡pointing ¡ to “rest ¡of ¡environment” “rest ¡of ¡environment” binding binding maps ¡variable ¡name ¡to ¡value maps ¡variable ¡name ¡to ¡value (define x 1) (define x 1) x 1 x 1 (define (f y) (lambda (y) (define (f y) (lambda (y) f f env (let ([x (+ y 1)]) env (let ([x (+ y 1)]) (lambda (z) (lambda (z) (let ([x (+ y 1)]) (let ([x (+ y 1)]) (+ x y z)) (+ x y z)) (lambda (z) (lambda (z) (+ x y z))) (+ x y z))) y y 4 4 x x 3 3 (define z (let ([x 3] (define z (let ([x 3] x 5 [g (f 4)] [g (f 4)] [y 5]) [y 5]) (g 6) )) (g 6) )) 3

9/18/15 Ex: ¡Returning ¡a ¡function Ex: ¡Returning ¡a ¡function env pointer env pointer shows ¡ env structure, ¡ by ¡pointing ¡ to shows ¡ env structure, ¡ by ¡pointing ¡ to “rest ¡of ¡environment” “rest ¡of ¡environment” binding binding maps ¡variable ¡name ¡to ¡value maps ¡variable ¡name ¡to ¡value (define x 1) (define x 1) x 1 x 1 (define (f y) (lambda (y) (define (f y) (lambda (y) f f env (let ([x (+ y 1)]) env (let ([x (+ y 1)]) (lambda (z) (lambda (z) (let ([x (+ y 1)]) (let ([x (+ y 1)]) (+ x y z)) (+ x y z)) (lambda (z) (lambda (z) (+ x y z))) (+ x y z))) y y 4 4 x x 3 3 (define z (let ([x 3] (define z (let ([x 3] x x 5 5 [g (f 4)] [g (f 4)] g g [y 5]) [y 5]) (lambda (z) (lambda (z) env env (+ x y z)) (+ x y z)) (g 6) )) (g 6) )) y 5 Ex: ¡Returning ¡a ¡function Ex: ¡Returning ¡a ¡function env pointer env pointer shows ¡ env structure, ¡ by ¡pointing ¡ to shows ¡ env structure, ¡ by ¡pointing ¡ to “rest ¡of ¡environment” “rest ¡of ¡environment” binding binding maps ¡variable ¡name ¡to ¡value maps ¡variable ¡name ¡to ¡value (define x 1) (define x 1) x 1 x 1 (define (f y) (lambda (y) (define (f y) (lambda (y) f f env (let ([x (+ y 1)]) env (let ([x (+ y 1)]) (lambda (z) (lambda (z) (let ([x (+ y 1)]) (let ([x (+ y 1)]) (+ x y z)) (+ x y z)) (lambda (z) (lambda (z) (+ x y z))) (+ x y z))) y y 4 4 x x 3 3 (define z (let ([x 3] (define z (let ([x 3] x x 5 5 [g (f 4)] [g (f 4)] g g [y 5]) [y 5]) (lambda (z) (lambda (z) env env (+ x y z)) (+ x y z)) (g 6) )) y (g 6) )) y 5 5 z 6 z 6 eval z 15 4

9/18/15 Wh Why lexical ¡scope? Wh Why ¡ ¡lexical ¡scope? Lexical ¡scope : use ¡environment ¡ where ¡ function ¡is ¡defined 1. Function ¡meaning ¡ does ¡not ¡depend ¡on ¡variable ¡names. Example: ¡change ¡body ¡of ¡ f to ¡replace ¡ x with ¡ q. • Lexical ¡scope: ¡it ¡cannot ¡matter Dynamic ¡scope : use ¡environment ¡where ¡ function ¡is ¡called • Dynamic ¡scope: ¡depends ¡how ¡result ¡is ¡used (define (f y) History ¡has ¡shown ¡that ¡lexical ¡scope ¡is ¡almost ¡always ¡better. (let ([x (+ y 1)]) (lambda (z) (+ x y z)))) Here ¡are ¡ some ¡precise, ¡technical ¡reasons ¡(not ¡opinion). Example: ¡remove ¡unused ¡ variables. • Dynamic ¡scope: ¡but ¡maybe ¡some ¡ g uses ¡it ¡(weird). (define (f g) (let ([x 3]) (g 2))) Wh Why lexical ¡scope? Wh Why lexical ¡scope? 2. ¡ ¡Functions ¡can ¡be ¡understood ¡fully ¡where ¡defined. 3. ¡ ¡ ¡Closures ¡automatically ¡ “remember” ¡ the ¡data ¡they ¡need. More ¡examples, ¡idioms ¡later. Example: ¡dynamic ¡scope ¡tries ¡to ¡add ¡ #f , ¡unbound ¡variable ¡ y , ¡and ¡ 4. (define (greater-than-x x) (lambda (y) (> y x))) (define (f y) (define (no-negs xs) (let ([x (+ y 1)]) ( filter (greater-than-x -1) xs)) (lambda (z) (+ x y z)) (define x #f) (define (all-greater xs n) (define g (f 7)) ( filter (lambda (x) (> x n)) xs)) (define a (g 4)) 5