FIRST Sets Dr. Mattox Beckman University of Illinois at - PowerPoint PPT Presentation

Objectives FIRST Sets Examples FIRST Sets Dr. Mattox Beckman University of Illinois at Urbana-Champaign Department of Computer Science

Objectives FIRST Sets Examples Objectives ◮ Compute the FIRST sets for the nonterminal symbols of a grammar.

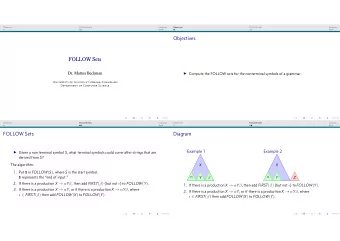
Objectives FIRST Sets Examples The Problem ◮ Given a grammar for a language L , how can we recognize a sentence in L ? ◮ Solution: Divide and conquer: Given a symbol E ... ◮ What symbols indicate that the symbol E is just starting? (FIRST Set) ◮ What symbols should we expect to see after we have fjnished parsing an E ? Misleadingly simple example: S → xEy FIRST( E ) = { z , q } E → zE FOLLOW( E )= { y } E → q ◮ Important because a parser can see only a few tokens at once.

Objectives FIRST Sets Examples Algorithm We can compute the FIRST set by a simple iterative algorithm. For each symbol X : 1. If X is a terminal, then FIRST ( X ) = { X } . 2. If there is a production X → ǫ , then add ǫ to FIRST ( X ) . 3. If there is a production X → Y 1 Y 2 · · · Y n , then add FIRST ( Y 1 Y 2 · · · Y n ) to FIRST ( X ) : ◮ If FIRST ( Y 1 ) does not contain ǫ , then FIRST ( Y 1 Y 2 · · · Y n ) = FIRST ( Y 1 ) . ◮ Otherwise, FIRST ( Y 1 Y 2 · · · Y n ) = FIRST ( Y 1 )/ ǫ ∪ FIRST ( Y 2 · · · Y n ) . ◮ If all of Y 1 , Y 2 , . . . Y n have ǫ then add ǫ to FIRST ( X ) .

Objectives FIRST Sets Examples Diagram X → Y 0 Y 1 Y 2 X Y 0 Y 1 Y 2 ◮ If there is a production X → Y 1 Y 2 · · · Y n , then add FIRST ( Y 1 Y 2 · · · Y n ) to FIRST ( X ) : ◮ If FIRST ( Y 1 ) does not contain ǫ , then FIRST ( Y 1 Y 2 · · · Y n ) = FIRST ( Y 1 ) . ◮ Otherwise, FIRST ( Y 1 Y 2 · · · Y n ) = FIRST ( Y 1 )/ ǫ ∪ FIRST ( Y 2 · · · Y n ) . ◮ If all of Y 1 , Y 2 , . . . Y n have ǫ then add ǫ to FIRST ( X ) .

Objectives FIRST Sets Examples Small Examples Example 1 Example 3 S → x A B B → A q B → r FIRST set of S is { x } . FIRST set of B is { y , z , q , r } . Example 2 Example 4 A → ǫ C → A A A → y C → B A → z q FIRST set of C is { y , z , q , r , ǫ } . FIRST set of A is { y , z , ǫ } .

Objectives FIRST Sets Examples FIRST Set Example Grammar Result S={} S → if E then S ; E={} S → print E ; P={} E → E + E E → P id P → ∗ P P → ǫ Action Step 1: Create a list of symbols.

Objectives FIRST Sets Examples FIRST Set Example Grammar Result S={ if , print } S → if E then S ; ⇐ E={} S → print E ; ⇐ P={ ǫ , * } E → E + E E → P id P → ∗ P ⇐ P → ǫ ⇐ Action Step 2: Add terminals starting productions, and all ǫ .

Objectives FIRST Sets Examples FIRST Set Example Grammar Result S={ if , print } S → if E then S ; E={ * , id } S → print E ; P={ ǫ , * } E → E + E E → P id ⇐ P → ∗ P P → ǫ Action Step 3: Check productions. Add FIRST ( P id ) to FIRST ( E ) .

Objectives FIRST Sets Examples FIRST Set Example Grammar Result S={ if , print } S → if E then S ; E={ * , id } S → print E ; P={ ǫ , * } E → E + E ⇐ E → P id P → ∗ P P → ǫ Action Step 4: Check productions: E → E + E adds nothing. We’re done.

Objectives FIRST Sets Examples Another FIRST Set Example Grammar Result S ={} S → A x A={} S → B y B={} S → z C={} A → 1 CB A → 2 B B → 3 B B → C C → 4 C → ǫ Action Create a chart.

Objectives FIRST Sets Examples Another FIRST Set Example Grammar Result S ={ z} S → A x A={ 1, 2} S → B y B={ 3} S → z ⇐ C={ ǫ , 4} A → 1 CB ⇐ A → 2 B ⇐ B → 3 B ⇐ B → C C → 4 ⇐ C → ǫ ⇐ Action Add initial terminals and ǫ s.

Objectives FIRST Sets Examples Another FIRST Set Example Grammar Result S ={z, 1, 2} S → A x ⇐ A={1, 2} S → B y B={3} S → z C={ ǫ , 4} A → 1 CB A → 2 B B → 3 B B → C C → 4 C → ǫ Action Add FIRST ( A x ) to FIRST ( S ) .

Objectives FIRST Sets Examples Another FIRST Set Example Grammar Result S ={z, 1, 2, 3} S → A x A={1, 2} S → B y ⇐ B={3} S → z C={ ǫ , 4} A → 1 CB A → 2 B B → 3 B B → C C → 4 C → ǫ Action Add FIRST ( B y ) to FIRST ( S ) . Note that there is still more to be added to FIRST ( B ) ! We will have to revisit this step later.

Objectives FIRST Sets Examples Another FIRST Set Example Grammar Result S ={z, 1, 2, 3} S → A x A={1, 2} S → B y B={3, 4, ǫ } S → z C={ ǫ , 4} A → 1 CB A → 2 B B → 3 B B → C ⇐ C → 4 C → ǫ Action Add FIRST ( C ) to FIRST ( B ) . At this point we should iterate again to see if anything changes.

Objectives FIRST Sets Examples Another FIRST Set Example Grammar Result S ={z, 1, 2, 3} S → A x ⇐ A={1, 2} S → B y B={3, 4, ǫ } S → z C={ ǫ , 4} A → 1 CB A → 2 B B → 3 B B → C C → 4 C → ǫ Action Add FIRST ( A x ) to FIRST ( S ) again. Nothing happens ...

Objectives FIRST Sets Examples Another FIRST Set Example Grammar Result S ={z, 1, 2, 3, 4, y} S → A x A={1, 2} S → B y ⇐ B={3, 4, ǫ } S → z C={ ǫ , 4} A → 1 CB A → 2 B B → 3 B B → C C → 4 C → ǫ Action Add FIRST ( B y ) to FIRST ( S ) again. The 4 gets propagated. Since B could be ǫ we need to add y .

Objectives FIRST Sets Examples Another FIRST Set Example Grammar Result S ={z, 1, 2, 3, 4, y} S → A x A={1, 2} S → B y B={3, 4, ǫ } S → z C={ ǫ , 4} A → 1 CB A → 2 B B → 3 B B → C ⇐ C → 4 C → ǫ Action Add FIRST ( C ) to FIRST ( B ) again. We are done.