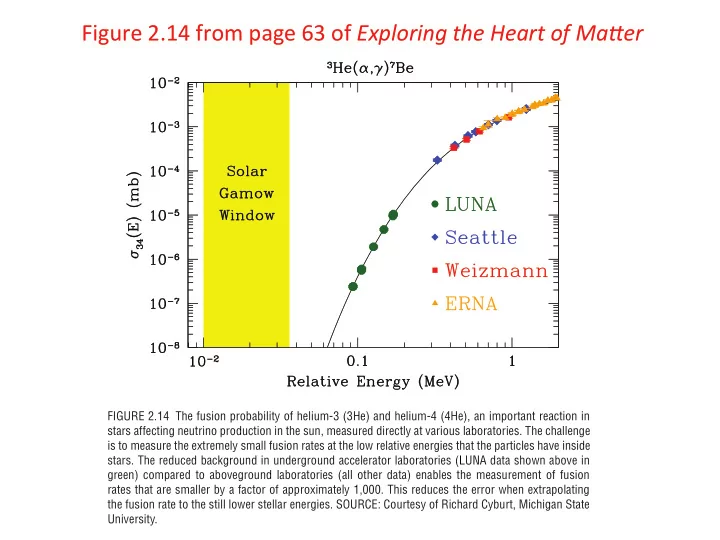
Figure 2.14 from page 63 of Exploring the Heart of Ma2er - PowerPoint PPT Presentation

Figure ¡2.14 ¡from ¡page ¡63 ¡of ¡ Exploring ¡the ¡Heart ¡of ¡Ma2er ¡ FIGURE 2.14 The fusion probability of helium-3 (3He) and helium-4 (4He), an important reaction in stars affecting neutrino production in the sun, measured directly at various laboratories. The challenge is to measure the extremely small fusion rates at the low relative energies that the particles have inside stars. The reduced background in underground accelerator laboratories (LUNA data shown above in green) compared to aboveground laboratories (all other data) enables the measurement of fusion rates that are smaller by a factor of approximately 1,000. This reduces the error when extrapolating the fusion rate to the still lower stellar energies. SOURCE: Courtesy of Richard Cyburt, Michigan State University.

2 $ ' r P = χ III 2 T ∝ 1 ∫ 2 ∝ exp − 2 k ( r ) dr & ) & ) χ I P % ( r 1 In the case of the Coulomb barrier, the above integral can be evaluated exactly. b log T = a + Q α Geiger-Nuttall law of alpha decay 1911 For the Coulomb barrier above, derive the Geiger-Nuttal law. Assume that the energy of an alpha particle is E=Q α , and that the outer turning point is much greater than the potential radius.

Reaction Rate Definition Reaction Rate Definition For a given relative velocity v with projectile number density n p [ ] − λ = σ ⋅ ⋅ 1 n v s reaction/target particle p energy/temperature dependent decay constant λ [ ] − = σ ⋅ ⋅ ⋅ ⋅ 1 R n v n V s p T reaction rate in volume V

Reaction Rate in Stellar Environment Reaction Rate in Stellar Environment reaction rate per second and cm 3 : = ⋅ ⋅ σ ⋅ r n n v p T Reaction rate for particles with velocity distribution Φ (v) 1 ∫ = ⋅ ⋅ σ ⋅ ⋅ Φ ⋅ ( ) r n n v v dv + δ p T 1 pT Accounting for reactions Between identical particles

Maxwell Boltzmann Distribution Maxwell Boltzmann Distribution In stellar material of temperature T particles follow ideal gas law ∫ 3 / 2 Φ = 2 ⎛ ⎞ v ( ) 1 m − m v dv Φ = π ⎜ ⎟ 2 ( ) 4 e 2 kT with v v ⎜ ⎟ π 2 ⎝ ⎠ kT 4 example: in terms 3 of energy arbitrary units E=1/2 m v 2 max at E=kT 2 1 0 0 20 40 60 80 energy (keV)

Temperature in Stars Temperature in Stars

Stellar reaction rates Stellar reaction rates 1 2 N = ρ < σ > 2 reactions per s and cm 3 r Y Y v A + δ T p 1 pT 1 λ = ρ < σ > N Y p v reactions per s & A + δ 1 Target nucleus pT this is usually referred to as the stellar reaction rate stellar reaction rate units of stellar reaction rate N A <sv>: usually cm 3 /s/mole X X T ; mass fraction = ρ ⋅ ⋅ = ρ ⋅ ⋅ T n N N Y Y T : abundance T A A T A T

Gamow- -Range & Reaction Rate Range & Reaction Rate Gamow Stellar Energy Range -- Gamow Window -- Resonance Width ∝ exp ( - E / kT ) ∝ exp ( - E / kT ) GAMOW PEAK RESONANCE σ ∝ exp ( - b / √ E ) Γ 2 σ ∝ ( E - E ) 2 2 + ( Γ / 2) Nonresonant Reaction Contributions ∫ σ : cross section -3/2 σ E N < σ v > ∝ T exp ( - E / kT ) d E A ωγ : res. strength Resonant Reaction Rate E R : res. energy -3/2 A < σ v > ∝ T ωγ N exp ( - E / kT ) R σ

The Gamow Range of Stellar Burning The Gamow Range of Stellar Burning The Gamow window or the range of relevant cross section for “non-resonant” processes is calculated: Check derivation in book 3 / 2 ( ) ⎛ ⎞ bkT 1 / 3 = = ⋅ 2 2 2 / 3 ⎜ ⎟ 0 . 122 MeV E Z Z A T 0 1 2 9 ⎝ 2 ⎠ ( ) 4 1 / 6 Δ = = ⋅ 2 2 5 / 6 0 . 2368 MeV E E kT Z Z A T 0 1 2 9 3 with A “reduced mass number” and T 9 the temperature in GK

γ ) C(p, γ The Gamow peak for 12 12 C(p, ) 13 13 N N The Gamow peak for Note: kT=2.5 keV !

Examples of Gamow window energies Examples of Gamow window energies 10.00 EG amow [M eV] p+p 12C+p 1.00 12C+a 0.10 12C+12C 0.01 0.0 0.1 1.0 10.0 strong dependence temperature [GK] on Z & temperature