Features of Statistical Parsers Preliminary results Mark Johnson - PowerPoint PPT Presentation

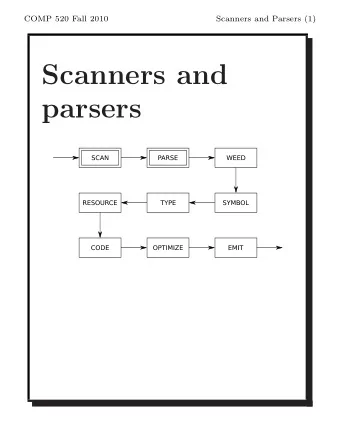
Features of Statistical Parsers Preliminary results Mark Johnson Brown University TTI, October 2003 Joint work with Michael Collins (MIT) Supported by NSF grants LIS 9720368 and IIS0095940 1

Talk outline • Statistical parsing from PCFGs to discriminative models • Linear discriminative models – conditional estimation and log loss – over-learning and regularization • Feature design – Local and non-local features – Feature design • Conclusions and future work 2

Why adopt a statistical approach? • The interpretation of a sentence is: – hidden , i.e., not straight-forwardly determined by its words or sounds – dependent on many interacting factors , including grammar, structural preferences, pragmatics, context and general world knowledge. – pervasively ambiguous even when all known linguistic and cognitive constraints are applied • Statistics is the study of inference under uncertainty – Statistical methods provide a systematic way of integrating weak or uncertain information 3

The dilemma of non-statistical CL 1. Ambiguity explodes combinatorially (162) Even though it’s possible to scan using the Auto Image Enhance mode, it’s best to use the normal scan mode to scan your documents. • Refining the grammar is usually self-defeating ⇒ splits states ⇒ makes ambiguity worse! • Preference information guides parser to correct analysis 2. Linguistic well-formedness leads to non-robustness • Perfectly comprehensible sentences receive no parses . . . 4

Conventional approaches to robustness • Some ungrammatical sentences are perfectly comprehensible e.g., He walk – Ignoring agreement ⇒ spurious ambiguity I saw the father of the children that speak(s) French • Extra-grammatical rules, repair mechanisms, . . . – How can semantic interpretation take place without a well-formed syntactic analysis? • A preference-based approach can provide a systematic treatment of robustness too! 5

Linguistics and statistical parsing • Statistical parsers are not “linguistics-free” – The corpus contains linguistic information (e.g., the treebank is based on a specific linguistic theory) – Linguistic and psycholinguistic insights guide feature design • What is the most effective way to import linguistic knowledge into a machine? – manually specify possible linguistic structures ∗ by explicit specification (a grammar) ∗ by example (an annotated corpus) – manually specify the model’s features – learn feature weights from training data 6

Framework of statistical parsing • X is the set of sentences • Y ( x ) is the set of possible linguistic analyses of x ∈ X • Preference or score S w ( x, y ) for each ( x, y ) parameterized by weights w • Parsing a string x involves finding the highest scoring analysis y ( x ) = argmax ˆ S w ( x, y ) y ∈Y ( x ) • Learning or training involves identifying w from data 7

PCFGs and the MLE S S S NP VP NP VP NP VP rice grows rice grows corn grows   S     NP VP rule count rel freq P  = 2 / 3    S → NP VP 3 1 rice grows NP → rice 2 2 / 3   S NP → corn 1 1 / 3     NP VP P  = 1 / 3   VP → grows 3 1  corn grows 8

Non-local constraints S S S NP VP NP VP NP VP rice grows rice grows bananas grow   S     NP VP P  = 4 / 9   rule count rel freq  rice grows S → NP VP 3 1 NP → rice 2 2 / 3   S NP → bananas 1 1 / 3     NP VP VP → grows 2 2 / 3 P   =  1 / 9  VP → grow 1 1 / 3 bananas grow Z = 5 / 9 9

Renormalization S S S NP VP NP VP NP VP rice grows rice grows bananas grow   S     NP VP P  = 4 / 9 4 / 5   rule count rel freq  rice grows S → NP VP 3 1 NP → rice 2 2 / 3   S NP → bananas 1 1 / 3     NP VP VP → grows 2 2 / 3 P   =  1 / 9 1 / 5  VP → grow 1 1 / 3 bananas grow Z = 5 / 9 10

Other values do better! S S S NP VP NP VP NP VP rice grows rice grows bananas grow   S     rule count rel freq NP VP P  = 2 / 6 2 / 3    S → NP VP 3 1 rice grows NP → rice 2 2 / 3   NP → bananas 1 1 / 3 S   VP → grows 2 1 / 2   NP VP P    = 1 / 6 1 / 3 VP → grow 1 1 / 2  bananas grow (Abney 1997) Z = 3 / 6 11

Make dependencies local – GPSG-style   rule count rel freq S NP VP S → 2 2 / 3   +singular +singular   NP VP   P = 2 / 3 +singular +singular   NP VP   S → 1 1 / 3 +plural +plural rice grows NP +singular → rice 2 1   S NP +plural → bananas 1 1     NP VP   P = 1 / 3 +plural +plural VP   +singular → grows 2 1   bananas grow VP +plural → grow 1 1 12

Generative vs. Discriminative models Generative models: features are context-free • rules (local trees) are “natural” features • the MLE of w is easy to compute (in principle) Discriminative models: features have unknown dependencies − no “natural” features − estimating w is much more complicated + features need not be local trees + representations need not be trees 13

Generative vs Discriminative training VP VP V NP VP PP see NP PP VP V NP P NP N P NP V see N with N people with N 100 × 2 × 1 × run people telescopes telescopes . . . × 2 / 105 × . . . . . . × 1 / 7 × . . . . . . × 2 / 7 × . . . . . . × 1 / 7 × . . . Rule count rel freq rel freq VP → V 100 100 / 105 4 / 7 VP → V NP 3 3 / 105 1 / 7 VP → VP PP 2 2 / 105 2 / 7 NP → N 6 6 / 7 6 / 7 NP → NP PP 1 1 / 7 1 / 7 14

Features in standard generative models • Lexicalization or head annotation captures subcategorization of lexical items and primitive world knowledge • Trained from Penn treebank corpus ( ≈ 40,000 trees, 1M words) • Sparse data is the big problem, so smoothing or generalization is most important! S sank sank → VB VP sank NP boat NP VP torpedo sank DT NN VB NP the torpedo sank boat the torpedo sank DT NN the boat the boat 15

Many useful features are non-local • Many desirable features are difficult to localize (i.e., express in terms of annotation on labels) – Verb-particle constructions Sam gave chocolates out/up/to Sandy – Head-to-head dependencies in coordinate structures [[ the students ] and [ the professor ]] ate a pizza • Some features seem inherently non-local – Heavy constituents prefer to be at the end Sam donated to the library a collection ? (that it took her years to assemble) – Parallelism in coordination Sam saw a man with a telescope and a woman with binoculars ? Sam [saw a man with a telescope and a woman] with binoculars 16

Framework for discriminative parsing sentence x • Generate candidate parses Y ( x ) for each sentence x Collins model 3 • Each parse y ∈ Y ( x ) is mapped y 1 . . . y k parses Y ( x ) to a feature vector f ( x, y ) • Each feature f j is associated with a weight w j f ( x, y 1 ) . . . f ( x, y k ) features • Define S ( x, y ) = w · f ( x, y ) • The highest scoring parse w · f ( x, y 1 ) . . . w · f ( x, y k ) scores S ( x, y ) y = argmax ˆ S ( x, y ) y ∈Y ( x ) is predicted correct 17

Log linear models • The log likelihood is a linear function of feature values • Y = set of syntactic structures (not necessarily trees) • f j ( y ) = number of occurences of j th feature in y ∈ Y (these features need not be conventional linguistic features) • w j are “feature weight” parameters m � S w ( y ) = w j f j ( y ) j =1 V w ( y ) = exp S w ( y ) y � Z w = V w ( y ) Y y ∈Y m � V w ( y ) P w ( y ) = , log P λ ( y ) = w j f j ( y ) − log Z w Z w j =1 18

PCFGs are log-linear models Y = set of all trees generated by grammar G f w ( y ) = number of times the j th rule is used in y ∈ Y p j = probability of j th rule in G w j = log p j   S   NP VP   f = [ 1 , 1 , 0 , 1 , 0 ]   ���� ���� ���� ���� ���� rice grows S → NP VP NP → rice NP → bananas VP → grows VP → grow m m � � p f j ( y ) P w ( y ) = = exp( w j f j ( ω )) where w j = log p j j j =1 j =1 19

ML estimation for log linear models D = y 1 , . . . , y n w � = argmax L D ( w ) y i w Y n � L D ( w ) = P w ( y i ) i =1 � � P w ( y ) = V w ( y ) V w ( y ′ ) V w ( y ) = exp w j f j ( y ) Z w = Z w y ′ ∈Y j • For a PCFG, � w is easy to calculate, but . . . • in general ∂L D /∂w j and Z w are intractable analytically and numerically • Abney (1997) suggests a Monte-Carlo calculation method 20

Conditional estimation and pseudo-likelihood The pseudo-likelihood of w is the conditional probability of the hidden part (syntactic structure) w given its visible part (yield or terminal string) x = X ( y ) (Besag 1974) Y ( x i ) = { y : X ( y ) = X ( y i ) } w = argmax PL D ( w ) � y i λ n � Y PL D ( w ) = P λ ( y i | x i ) i =1 V w ( y ) P w ( y | x ) = Z w ( x ) � � V w ( y ′ ) V w ( y ) = exp w j f j ( y ) Z w ( x ) = j y ′ ∈Y ( x ) 21