= = = f f BOB BOB meaning vectors of words not does like - PowerPoint PPT Presentation

— symbolically: dagger compact categories — Thm. [Kelly-Laplaza ’80; Selinger ’05] An equa- tional statement between expressions in dagger com- pact categorical language holds if and only if it is derivable in the graphical notation via homotopy . Thm. [Hasegawa-Hofmann-Plotkin; Selinger ’08] An equational statement between expressions in dag- ger compact categorical language holds if and only if it is derivable in the dagger compact category of fi- nite dimensional Hilbert spaces, linear maps, tensor product and adjoints .

— expressivity — Full-blown QM / QC course at Oxford: Quantum Computer Science – quantum circuits, MBQC, – quantum algorithms, – quantum cryptography, – quantum non-locality, ...

— expressivity — Full-blown QM / QC course at Oxford: Quantum Computer Science – quantum circuits, MBQC, – quantum algorithms, – quantum cryptography, – quantum non-locality, ... Lecture notes forthcoming as book (approx. 400 pp): Bob Coecke & Aleks Kissinger Picturing Quantum Processes Cambridge University Press

— kindergarten quantum mechanics: the experiment — Contest in problem solving between: • Children using quantum picturalism • Physics teachers using ordinary QM The children will win! BC (2010) Quantum picturalism . Contemporary Physics 51, 59–83.

— what is logic? —

— what is logic? — Pragmatic option: Logic is structure in language .

— what is logic? — Pragmatic option: Logic is structure in language . “Alice and Bob ate everything or nothing, then got sick.” connectives ( ∧ , ∨ ) : and, or negation ( ¬ ) : not (cf. nothing = not something) entailment ( ⇒ ) : then quantifiers ( ∀ , ∃ ) : every(thing) , some(thing) constants ( a , b ) : thing variable ( x ) : Alice, Bob predicates ( P ( x ) , R ( x , y )) : eating, getting sick truth valuation (0 , 1) : true, false ( ∀ z : Eat ( a , z ) ∧ Eat ( b , z )) ∧ ¬ ( ∃ z : Eat ( a , z ) ∧ Eat ( b , z )) ⇒ S ick ( a ) , S ick ( b )

— what is logic? — Pragmatic option: Logic is structure in language . “Alice and Bob ate everything or nothing, then got sick.” connectives ( ∧ , ∨ ) : and, or negation ( ¬ ) : not (cf. nothing = not something) entailment ( ⇒ ) : then quantifiers ( ∀ , ∃ ) : every(thing) , some(thing) constants ( a , b ) : thing variable ( x ) : Alice, Bob predicates ( P ( x ) , R ( x , y )) : eating, getting sick truth valuation (0 , 1) : true, false ( ∀ z : Eat ( a , z ) ∧ Eat ( b , z )) ∧ ¬ ( ∃ z : Eat ( a , z ) ∧ Eat ( b , z )) ⇒ S ick ( a ) , S ick ( b ) This is about truth. What about genuine meaning?

A SLIGHTLY DIFFERENT LANGUAGE FOR NATURAL LANGUAGE MEANING BC, Mehrnoosh Sadrzadeh & Stephen Clark (2010) Mathematical foundations for a compositional distributional model of meaning . arXiv:1003.4394

— the from-words-to-a-sentence process —

— the from-words-to-a-sentence process — Consider meanings of words , e.g. as vectors (cf. Google): ... word 1 word 2 word n

— the from-words-to-a-sentence process — What is the meaning the sentence made up of these? ... word 1 word 2 word n

— the from-words-to-a-sentence process — I.e. how do we / machines produce meanings of sentences ? ? ... word 1 word 2 word n

— the from-words-to-a-sentence process — I.e. how do we / machines produce meanings of sentences ? grammar ... word 1 word 2 word n

— the from-words-to-a-sentence process — Information flow within a verb: subject subject object object verb

— the from-words-to-a-sentence process — Information flow within a verb: subject subject object object verb Again we have: =

— pregoup grammar — Lambek’s residuated monoids (1950’s): b ≤ a ⊸ c ⇔ a · b ≤ c ⇔ a ≤ c � b

— pregoup grammar — Lambek’s residuated monoids (1950’s): b ≤ a ⊸ c ⇔ a · b ≤ c ⇔ a ≤ c � b or equivalently, a · ( a ⊸ c ) ≤ c ≤ a ⊸ ( a · c ) ( c � b ) · b ≤ c ≤ ( c · b ) � b

— pregoup grammar — Lambek’s residuated monoids (1950’s): b ≤ a ⊸ c ⇔ a · b ≤ c ⇔ a ≤ c � b or equivalently, a · ( a ⊸ c ) ≤ c ≤ a ⊸ ( a · c ) ( c � b ) · b ≤ c ≤ ( c · b ) � b Lambek’s pregroups (2000’s): a · − 1 a ≤ 1 ≤ − 1 a · a b − 1 · b ≤ 1 ≤ b · b − 1

— Lambek’s pregoup grammar — A A -1 -1 A A -1 -1 A A A A A A A A = = A A A A -1 -1 -1 -1 A A A A = = -1 -1 -1 -1 A A A A Jim Lambek mentioned this connection first to (to me) during a seminar on categorical quantum mechanics at McGill here in Montreal in 2004.

— Lambek’s pregoup grammar — For noun type n , verb type is − 1 n · s · n − 1 , so:

— Lambek’s pregoup grammar — For noun type n , verb type is − 1 n · s · n − 1 , so: n · − 1 n · s · n − 1 · n ≤ 1 · s · 1 ≤ s

— Lambek’s pregoup grammar — For noun type n , verb type is − 1 n · s · n − 1 , so: n · − 1 n · s · n − 1 · n ≤ 1 · s · 1 ≤ s

— Lambek’s pregoup grammar — For noun type n , verb type is − 1 n · s · n − 1 , so: n · − 1 n · s · n − 1 · n ≤ 1 · s · 1 ≤ s

— Lambek’s pregoup grammar — For noun type n , verb type is − 1 n · s · n − 1 , so: n · − 1 n · s · n − 1 · n ≤ 1 · s · 1 ≤ s Diagrammatic type reduction: -1 n s -1 n n n

— Lambek’s pregoup grammar — For noun type n , verb type is − 1 n · s · n − 1 , so: n · − 1 n · s · n − 1 · n ≤ 1 · s · 1 ≤ s Diagrammatic meaning: flow flow flow flow n n verb

— algorithm for meaning of sentences —

— algorithm for meaning of sentences — 1. Perform type reduction: ( word type 1) . . . ( word type n ) � sentence type

— algorithm for meaning of sentences — 1. Perform type reduction: ( word type 1) . . . ( word type n ) � sentence type 2. Interpret diagrammatic type reduction as linear map:     � �         f :: �→  � ii |   ⊗ id ⊗  � ii |             i i

— algorithm for meaning of sentences — 1. Perform type reduction: ( word type 1) . . . ( word type n ) � sentence type 2. Interpret diagrammatic type reduction as linear map:     � �         f :: �→  � ii |   ⊗ id ⊗  � ii |             i i 3. Apply this map to tensor of word meaning vectors: � − � → v 1 ⊗ . . . ⊗ − → f v n

— − Alice ⊗ − − − − → − − → not ⊗ − like ⊗ − − → − → does ⊗ − − → Bob —

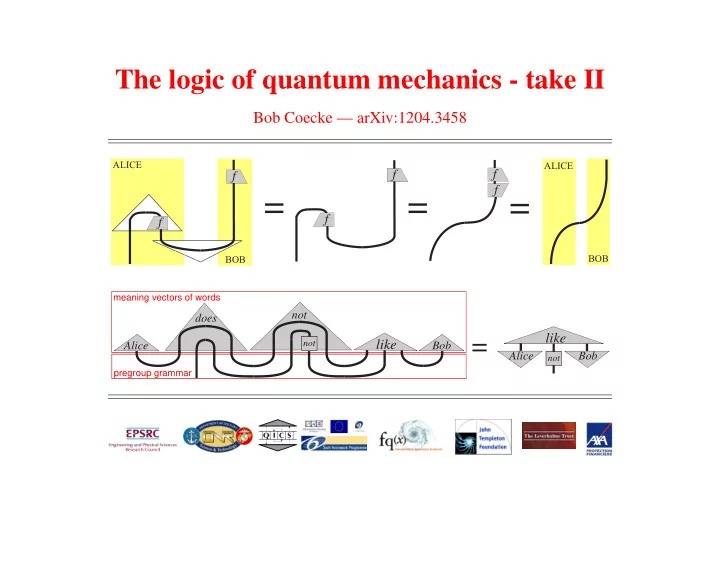
— − Alice ⊗ − − − − → − − → not ⊗ − like ⊗ − − → − → does ⊗ − − → Bob — grammar Alice Bob like not does not meaning vectors of words

— − Alice ⊗ − − − − → − − → not ⊗ − like ⊗ − − → − → does ⊗ − − → Bob — grammar Alice Bob like not meaning vectors of words

— − Alice ⊗ − − − − → − − → not ⊗ − like ⊗ − − → − → does ⊗ − − → Bob — grammar Alice Bob like not meaning vectors of words

— − Alice ⊗ − − − − → − − → not ⊗ − like ⊗ − − → − → does ⊗ − − → Bob — grammar Alice Bob like not meaning vectors of words not Alice Bob = like

— − Alice ⊗ − − − − → − − → not ⊗ − like ⊗ − − → − → does ⊗ − − → Bob — grammar Alice Bob like not meaning vectors of words not not Alice Bob = = like like Alice Bob Using: = = like like like like

CLASSICAL DATA i.e. BASIS

WIRES?

SPIDERS! B.C. and D. Pavlovic – arXiv:quant-ph / 0608035 B.C., D. Pavlovic and J. Vicary – arXiv:0810.0812 B.C., E.O. Paquette and D. Pavlovic – arXiv:0904.1997 B.C. and S. Perdrix – arXiv:1004.1598

— spiders —   m ....     � �������� �� �������� �           ‘spiders’ = ....         � �������� �� �������� �       n such that, for k > 0: m + m ′ − k .... .... .... � �������������������� �� �������������������� � .... = .... .... .... � �������������������� �� �������������������� � n + n ′ − k Coecke, Pavlovic & Vicary (2006, 2008) quant-ph/0608035 , 0810.0812

— spiders —   m ....     � �������� �� �������� �           ‘(co-)mult.’ = ....         � �������� �� �������� �       n such that, for k > 0: m + m ′ − k .... .... .... � �������������������� �� �������������������� � .... = .... .... .... � �������������������� �� �������������������� � n + n ′ − k

— spiders —   m ....     � �������� �� �������� �           ‘(co-)mult.’ = ....         � �������� �� �������� �       n such that, for k > 0: m + m ′ − k .... .... .... � �������������������� �� �������������������� � .... = .... .... .... � �������������������� �� �������������������� � n + n ′ − k

— spiders —   m ....     � �������� �� �������� �           ‘cups / caps’ = ....         � �������� �� �������� �       n such that, for k > 0: m + m ′ − k .... .... .... � �������������������� �� �������������������� � .... = .... .... .... � �������������������� �� �������������������� � n + n ′ − k Coecke, Pavlovic & Vicary (2006, 2008) quant-ph/0608035 , 0810.0812