Encoders Many 1-bit inputs, 1 asserted at a time. Output - PowerPoint PPT Presentation

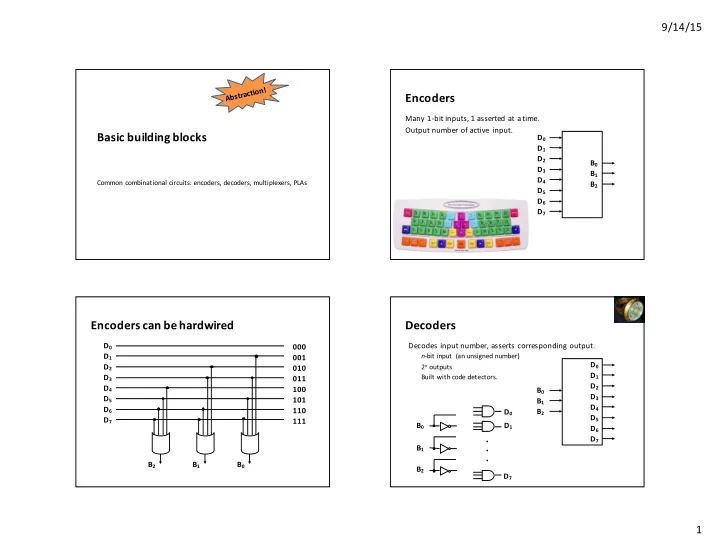
9/14/15 Encoders Many ¡1-­‑bit ¡inputs, ¡1 ¡asserted ¡at ¡a ¡time. Output ¡number ¡of ¡active ¡ input. Basic ¡building ¡blocks D 0 D 1 D 2 B 0 D 3 B 1 D 4 Common ¡combinational ¡circuits: ¡encoders, ¡decoders, ¡multiplexers, ¡PLAs B 2 D 5 D 6 D 7 Encoders ¡can ¡be ¡hardwired Decoders D 0 Decodes ¡input ¡number, ¡asserts ¡corresponding ¡output. 000 D 1 n -­‑bit ¡input ¡ ¡(an ¡unsigned ¡number) 001 D 0 2 n outputs D 2 010 D 1 D 3 Built ¡with ¡code ¡detectors. 011 D 2 D 4 100 B 0 D 3 D 5 101 B 1 D 4 D 6 110 B 2 D 0 D 5 D 7 111 B 0 D 1 D 6 . ¡ D 7 . ¡ B 1 . B 2 B 1 B 0 B 2 D 7 1

9/14/15 Ta ¡da! Steering ¡circuits Many ¡possible ¡output ¡destinatinons. Many ¡possible ¡input ¡sources. Multiplexer Demultiplexer Select ¡ one Select ¡ one Multipexers 8-­‑to-­‑1 ¡MUX 2 n data ¡inputs D 0 1 ¡data ¡output D 1 n control/selector ¡lines. D 2 D 3 MUX F D 4 D 5 D 6 World's ¡smallest ¡mux: D 7 A B C Costume ¡idea: ¡MUX ¡OX 2

9/14/15 MUX ¡+ ¡voltage ¡source ¡= ¡truth ¡table Buses ¡and ¡Logic ¡Arrays Bitwise ¡operations ¡apply ¡the ¡same ¡function ¡ to ¡each ¡bit ¡of ¡an ¡entire ¡word. A ¡ bus is ¡a ¡collection ¡of ¡data ¡lines ¡that ¡is ¡ A B C Majority D 0 treated ¡as ¡a ¡single ¡logical ¡signal. D 1 0 0 0 0 Array ¡of ¡logic ¡elements ¡ shows ¡same ¡ D 2 0 0 1 0 operation ¡applied ¡to ¡each ¡bit ¡in ¡a ¡bus. D 3 0 1 0 0 Mux F D 4 0 1 1 1 D 5 1 0 0 0 D 6 D 7 1 0 1 1 1 1 0 1 A B C 1 1 1 1 PLAs PLA ¡example A ¡ programmable ¡logic ¡array (PLA) ¡has ¡a ¡ set ¡of ¡inputs ¡and ¡corresponding ¡input ¡ complements ¡and ¡two ¡stages ¡of ¡logic. The ¡first ¡state ¡is ¡an ¡array ¡of ¡AND ¡gates ¡ which ¡form ¡the ¡product ¡terms ¡ ( minterms ). The ¡second ¡stage ¡is ¡an ¡array ¡of ¡OR ¡gates ¡ that ¡sums ¡the ¡minterms. Remember ¡ sum ¡of ¡products? 3

9/14/15 Gray ¡Codes ¡= ¡reflected ¡binary ¡codes PLAs: ¡Another ¡drawing ¡convention Alternate ¡ encoding ¡for ¡unsigned ¡integers AND ¡plane: designed ¡for ¡electromechanical ¡ switches ¡and ¡counting. Each ¡vertical ¡ line ¡= ¡AND ¡gate. Dots ¡show ¡connected ¡inputs. 00 ¡ ¡ ¡01 ¡ ¡ ¡11 ¡ ¡ ¡10 As ¡a ¡ROM: input ¡= ¡address 000 ¡ ¡ ¡001 ¡ ¡ ¡011 ¡ ¡ ¡010 ¡ ¡ ¡110 ¡ ¡ ¡111 ¡ ¡ ¡101 ¡ ¡ ¡100 output ¡= ¡contents How ¡many ¡ bits ¡change ¡when ¡incrementing? OR ¡plane: Each ¡horizontal ¡line ¡= ¡OR ¡gate. Dots ¡show ¡connected ¡inputs. Karnaugh Maps: find ¡minimal ¡ sums ¡of ¡products ¡visually CD gray ¡code A B C D F(A, ¡B, ¡C, ¡D) 00 01 11 10 order 0 0 0 0 0 0 0 0 1 0 00 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 1 0 0 0 01 0 0 0 1 0 1 0 1 0 AB 0 1 1 0 1 0 1 1 1 0 11 1 1 0 1 1 0 0 0 1 1 0 0 1 1 10 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 0 0 1 1. Cover ¡exactly ¡the ¡1s ¡by ¡drawing ¡maximally ¡sized ¡rectangles ¡ 1 1 0 1 1 whose ¡dimensions ¡(in ¡cells) ¡are ¡powers ¡of ¡2. ¡ ¡(May ¡wrap!) 1 1 1 0 1 2. For ¡each ¡box, ¡make ¡a ¡product ¡of ¡the ¡inputs ¡(or ¡complements) ¡ 1 1 1 1 0 that ¡are ¡ 1 ¡for ¡all ¡cells ¡in ¡the ¡box. ¡(minterms) 3. T ake ¡ the ¡sum ¡of ¡these ¡products. 4