Dynamical Systems in Problems of Gene Regulation Peter Schuster - PowerPoint PPT Presentation

Dynamical Systems in Problems of Gene Regulation Peter Schuster Institut für Theoretische Chemie, Universität Wien, Austria and The Santa Fe Institute, Santa Fe, New Mexico, USA CAS-MPG Partner Institute for Computational Biology Shanghai, 26.10.2007

Web-Page for further information: http://www.tbi.univie.ac.at/~pks

1. The problems of quantitative biology 2. Forward and inverse problems in reaction kinetics 3. Regulation kinetics and bifurcation analysis 4. Reverse engineering of dynamical systems 5. How to upscale from small models to cells?

1. The problems of quantitative biology 2. Forward and inverse problems in reaction kinetics 3. Regulation kinetics and bifurcation analysis 4. Reverse engineering of dynamical systems 5. How to upscale from small models to cells?

A model genome with 12 genes 1 2 3 4 5 6 7 8 9 10 11 12 Regulatory protein or RNA Regulatory gene Enzyme Structural gene Metabolite Sketch of a genetic and metabolic network

A B C D E F G H I J K L Biochemical Pathways 1 2 3 4 5 6 7 8 9 10 The reaction network of cellular metabolism published by Boehringer-Ingelheim.

The citric acid or Krebs cycle (enlarged from previous slide).

The bacterial cell as an example for the simplest form of autonomous life The human body: 10 14 cells = 10 13 eukaryotic cells + � 9 � 10 13 bacterial (prokaryotic) cells, and � 200 eukaryotic cell types The spatial structure of the bacterium Escherichia coli

1. The problems of quantitative biology 2. Forward and inverse problems in reaction kinetics 3. Regulation kinetics and bifurcation analysis 4. Reverse engineering of dynamical systems 5. How to upscale from small models to cells?

Kinetic differential equations d x = = = ( ; ) ; ( , , ) ; ( , , ) K K f x k x x x k k k 1 1 n m d t Reaction diffusion equations ∂ x = ∇ + 2 ( ; ) Solution curves : ( ) D x f x k x t ∂ t x i (t) Concentration Parameter set = ( T , p , p H , I , ) ; j 1 , 2 , , m K K k j General conditions : T , p , pH , I , ... t ( 0 ) Initial conditions : x Time Boundary conditions : � boundary ... S , normal unit vector ... u x S = Dirichlet : ( , ) g r t ∂ S = x = ⋅ ∇ ˆ Neumann : ( , ) u x g r t ∂ u The forward problem of chemical reaction kinetics (Level I)

Kinetic differential equations d x = = = ( ; ) ; ( , , ) ; ( , , ) K K f x k x x x k k k 1 1 n m d t Reaction diffusion equations ∂ x 2 = ∇ + Genome: Sequence I G ( ; ) Solution curves : ( ) D x f x k x t ∂ t x i (t) Concentration Parameter set = ( G I ; , , , , ) ; 1 , 2 , , K K k j T p p H I j m General conditions : T , p , pH , I , ... t ( 0 ) Initial conditions : x Time Boundary conditions : boundary ... S , normal unit vector � ... u x S = Dirichlet : ( , ) g r t ∂ S = x = ⋅ ∇ ˆ ( , ) Neumann : u x g r t ∂ u The forward problem of biochemical reaction kinetics (Level I)

Kinetic differential equations d x = = = ( ; ) ; ( , , ) ; ( , , ) K K f x k x x x k k k 1 1 n m d t Reaction diffusion equations ∂ x = ∇ + 2 ( ; ) D x f x k ∂ t General conditions : T , p , pH , I , ... ( 0 ) Initial conditions : x Genome: Sequence I G Boundary conditions : boundary ... S , normal unit vector � ... u Parameter set x S = = Dirichlet : ( , ) ( G I ; , , , , ) ; 1 , 2 , , g r t K K k j T p p H I j m ∂ S = x = ⋅ ∇ Neumann : ˆ ( , ) u x g r t ∂ u Data from measurements (t ); = 1, 2, ... , x j N j x i (t ) j Concentration The inverse problem of biochemical t Time reaction kinetics (Level I)

Kinetic differential equations d x = = = f ( ; ) ; ( , , ) ; ( , , ) K K x k x x x k k k 1 1 n m d t Bifurcation analysis Reaction diffusion equations � ( , ; ) ∂ k k j k i x = ∇ 2 + f ( ; ) Genome: Sequence I G D x x k ∂ t k i P x n P Parameter set x n P x m = ( G I ; , , , , ) ; 1 , 2 , , K K k j T p p H I j m x m ( ) x t General conditions : T , p , pH , I , ... P time ( 0 ) Initial conditions : x x n x m k j Boundary conditions : boundary ... S , normal unit vector � ... u x S = Dirichlet : ( , ) g r t ∂ S = x = ⋅ ∇ ˆ Neumann : ( , ) u x g r t ∂ u The forward problem of bifurcation analysis (Level II)

Kinetic differential equations d x = = = ( ; ) ; ( , , ) ; ( , , ) f x k x x K x k k K k 1 1 n m d t Reaction diffusion equations ∂ x = ∇ + 2 ( ; ) D x f x k ∂ t General conditions : T , p , pH , I , ... ( 0 ) Initial conditions : x Genome: Sequence I G Boundary conditions : � boundary ... S , normal unit vector ... u Parameter set x S = = Dirichlet : ( , ) ( G I ; , , , , ) ; 1 , 2 , , g r t K K k j T p p H I j m ∂ S = x Neumann : = ⋅ ∇ ˆ ( , ) u x g r t ∂ u Bifurcation pattern � ( , ; ) k k j k i k 2 P 1 x n P 2 x P x m x The inverse problem of bifurcation P analysis (Level II) x k 1 x

1. The problems of quantitative biology 2. Forward and inverse problems in reaction kinetics 3. Regulation kinetics and bifurcation analysis 4. Reverse engineering of dynamical systems 5. How to upscale from small models to cells?

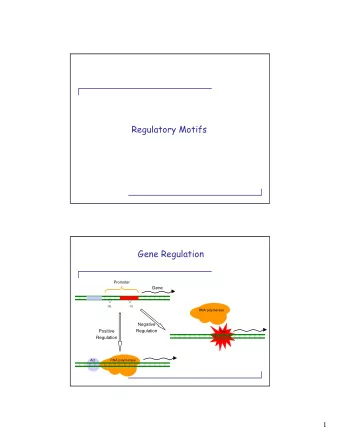
Active states of gene regulation

Promotor III State : inactive state Repressor Activator binding site RNA polymerase Promotor III State : inactive state Activator Repressor RNA polymerase Inactive states of gene regulation

synthesis degradation Cross-regulation of two genes

n p = Activation : ( ) j F p + n i j K p j K = Repression : ( ) F p + n i j K p j = , 1 , 2 i j Gene regulatory binding functions

= = = dq [ G ] [ G ] const . g = Q − Q 1 ( ) 1 2 0 k F p d q 1 1 2 1 1 = = [ Q ] , [ Q ] , dt q q 1 1 2 2 = = [ P ] , [ P ] p p dq = − 1 1 2 2 Q Q 2 ( ) k F p d q 2 2 1 2 2 dt n p = Activation : ( ) j F p dp + i j n = − P P K p 1 k q d p j 1 1 2 1 dt K = Repression : ( ) F p + n i j dp K p = − P P 2 j k q d p 2 2 2 2 = , 1 , 2 dt i j − ϑ ϑ = = ϑ Stationary points : ( ( )) 0 , ( ) p F F p p F p 1 1 1 2 2 1 2 2 2 1 Q P Q P k k k k ϑ = ϑ = 1 1 , 2 2 1 2 Q P Q P d d d d 1 1 2 2 Qualitative analysis of cross-regulation of two genes: Stationary points

∂ ∂ ⎛ ⎞ F F ⎜ 1 1 ⎟ Q Q k k − 1 1 ∂ ∂ 0 Q d ⎜ ⎟ p p 1 1 2 ⎧ ⎫ ∂ ∂ ⎜ ⎟ ∂ ⎪ ⎪ − & 0 F F Q x d 2 2 Q Q = = = A ⎨ ⎬ 2 k k i ⎜ ⎟ a 2 2 ∂ ∂ ∂ ⎪ ij ⎪ p p x ⎩ ⎭ ⎜ ⎟ 1 2 j − 0 0 P P ⎜ ⎟ k d 1 1 ⎜ ⎟ − 0 0 P P ⎝ ⎠ k d 2 2 ∂ ∂ F F = = Cross regulation : 1 2 0 ∂ ∂ p p 1 2 ∂ F − − ε 0 0 1 Q Q d k 1 1 ∂ p 2 ∂ F Q Q − − ε 2 0 Q Q 0 ε = = A - I D K d k 2 2 ∂ p P P 1 D K − − ε 0 0 P P k d 1 1 − − ε 0 0 P P k d 2 2 Qualitative analysis of cross-regulation of two genes: Jacobian matrix

Q Q ⋅ = ⋅ D K = ⋅ − ⋅ and hence Q P P Q Q P Q P D K K D D D K K P P K D ( )( ) ∂ F − − ε − − ε − 1 Q P Q P d d k k 1 1 1 1 ∂ p ⋅ − ⋅ = = Q P Q P 2 ∂ ( )( ) D D K K F − − − ε − − ε 2 Q P Q P k k d d 2 2 2 2 ∂ p 1 ( )( )( )( ) ∂ ∂ F F = − − ε − − ε − − ε − − ε − = 1 2 0 Q P Q P Q Q P P d d d d k k k k 1 1 2 2 1 2 1 2 ∂ ∂ p p 2 1 + Q + Q + P + P + = ( ε ) ( ε ) ( ε ) ( ε ) 0 d d d d D 1 2 1 2 ∂ ∂ F F = − Q Q P P 1 2 D k k k k 1 2 1 2 ∂ ∂ x x 2 1

+ + + + + = Q Q P P ( ε ) ( ε ) ( ε ) ( ε ) 0 d d d d D 1 2 1 2 ∂ ∂ F F Eigenvalues of the Jacobian of the = − Q Q P P 1 2 D k k k k 1 2 1 2 ∂ ∂ cross-regulatory two gene system x x 2 1

= − Q Q P P D d d d d OneD 1 2 1 2 + + + + + + Q Q Q P Q P Q P Q P P P ( )( )( )( )( )( ) d d d d d d d d d d d d = 1 2 1 1 1 2 2 1 2 2 1 2 D Hopf + + + Q Q P P 2 ( ) d d d d 1 2 1 2

Regulatory dynamics at D � 0 , act.-act., n=2

Regulatory dynamics at D � 0 , act.-rep., n=3

Regulatory dynamics at D < D Hopf , act.-repr., n=3

Regulatory dynamics at D > D Hopf , act.-repr., n=3

Regulatory dynamics at D � 0 , rep.-rep., n=2

Hill coefficient: n Act.-Act. Act.-Rep. Rep.-Rep. 1 S , E S S 2 E , B(E,P) S S , B(P 1 ,P 2 ) 3 E , B(E,P) S , O S , B(P 1 ,P 2 ) 4 E , B(E,P) S , O S , B(P 1 ,P 2 )