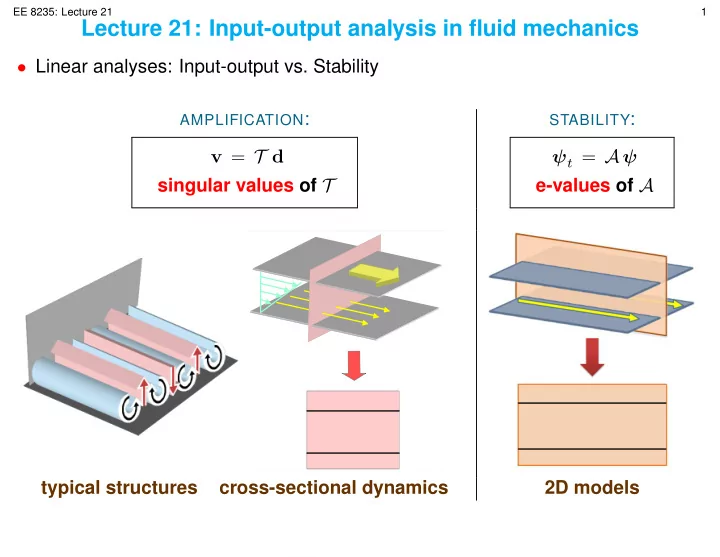
Draft EE 8235: Lecture 21 1 Lecture 21: Input-output analysis in - PowerPoint PPT Presentation

Draft EE 8235: Lecture 21 1 Lecture 21: Input-output analysis in fluid mechanics • Linear analyses: Input-output vs. Stability AMPLIFICATION : STABILITY : v = T d ψ t = A ψ singular values of T e-values of A typical structures typical structures cross-sectional dynamics 2D models

Draft EE 8235: Lecture 21 2 Transition in Newtonian fluids • L INEAR HYDRODYNAMIC STABILITY : unstable normal modes ⋆ successful in: Benard Convection, Taylor-Couette flow, etc. ⋆ fails in: wall-bounded shear flows (channels, pipes, boundary layers) • D IFFICULTY #1 Inability to predict: Reynolds number for the onset of turbulence ( Re c ) � much before instability Experimental onset of turbulence: no sharp value for Re c • D IFFICULTY #2 Inability to predict: flow structures observed at transition (except in carefully controlled experiments)

Draft EE 8235: Lecture 21 3 L INEAR STABILITY : • ⋆ For Re ≥ Re c ⇒ exp. growing normal modes � corresponding e-functions := exp. growing flow structures (TS-waves) ∞ ∞ z • ✂✂ ✍ ✲ x E XPERIMENTS : streaky boundary layers and turbulent spots • Flow z z ✻ ✻ ✲ ✲ x x Matsubara & Alfredsson, J. Fluid Mech. ’01

Draft EE 8235: Lecture 21 4 • F AILURE OF LINEAR HYDRODYNAMIC STABILITY caused by high flow sensitivity ⋆ large transient responses ⋆ large noise amplification ⋆ small stability margins TO COUNTER THIS SENSITIVITY : must account for modeling imperfections T RANSITION ≈ S TABILITY + R ECEPTIVITY + R OBUSTNESS − − ← ← flow unmodeled disturbances dynamics

Draft EE 8235: Lecture 21 5 Tools for quantifying sensitivity • I NPUT - OUTPUT ANALYSIS : spatio-temporal frequency responses  Free-stream turbulence  � Surface roughness Fluctuating d v  Acoustic waves velocity field ✲ Linearized Dynamics ✲     d 1 u amplification d 2 v − − − − − − − − − − − →     d 3 w � �� � � �� � v d IMPLICATIONS FOR : transition: insight into mechanisms control: control-oriented modeling

Draft EE 8235: Lecture 21 6 Ensemble average energy density Re = 2000 • Dominance of streamwise elongated structures streamwise streaks!

Draft EE 8235: Lecture 21 7 Influence of Re : streamwise-constant model �   � � � d 1 � � � � A os 0 ψ 1 t ψ 1 0 B 2 B 3 = + d 2   ψ 2 t ψ 2 B 1 0 0 Re A cp A sq d 3     u 0 C u � � ψ 1  = v C v 0    ψ 2 w C w 0 d 1 ✲ B 1 coupling Squire Orr-Sommerfeld ψ 1 ψ 2 d 2 u ❄ ✲ (j ωI − A os ) − 1 ✲ (j ωI − A sq ) − 1 ✲ ReA cp ✲ B 2 ✲ ♥ ✲ ♥ ✲ C u ✲ s ✻ d 3 v ✲ C v ✲ ✲ B 3 s w ✲ C w ✲ Jovanovi´ c & Bamieh, J. Fluid Mech. ’05

Draft EE 8235: Lecture 21 8 Amplification mechanism in flows with high Re • H IGHEST AMPLIFICATION : ( d 2 , d 3 ) → u ‘glorified vortex viscous diffusion’ tilting dissipation ψ 1 ReA cp ψ 2 d 2 u ✲ (j ωI − ∆) − 1 ✲ (j ωI − ∆ − 1 ∆ 2 ) − 1 ✲ B 2 ✲ ♥ ✲ ✲ C u ✲ ✻ d 3 ✲ B 3 ☞ A MPLIFICATION MECHANISM : vortex tilting or lift-up wall-normal direction spanwise direction

Draft EE 8235: Lecture 21 9 Turbulence without inertia N EWTONIAN : inertial turbulence V ISCOELASTIC : elastic turbulence Groisman & Steinberg, Nature ’00 N EWTONIAN : V ISCOELASTIC : ☞ F LOW RESISTANCE : increased 20 times!

Draft EE 8235: Lecture 21 10 Turbulence: good for mixing . . . Groisman & Steinberg, Nature ’01

EE 8235: Lecture 21 R ECTILINEAR FLOWS : no modal instabilities C URVILINEAR FLOWS : purely elastic instabilities P OLYMER MELT EMERGING FROM A CAPILLARY TUBE Draft . . . bad for processing Larson, Shaqfeh, Muller, J. Fluid Mech. ’90 Kalika & Denn, J. Rheol. ’87 11

Draft EE 8235: Lecture 21 12 Oldroyd-B fluids H OOKEAN SPRING : ( Re/We ) v t = − Re ( v · ∇ ) v − ∇ p + β ∆ v + (1 − β ) ∇ · τ + d 0 = ∇ · v � � τ t = − τ + ∇ v + ( ∇ v ) T + We τ · ∇ v + ( ∇ v ) T · τ − ( v · ∇ ) τ β := solvent viscosity V ISCOSITY RATIO : total viscosity fluid relaxation time W EISSENBERG NUMBER : We := characteristic flow time Re := inertial forces R EYNOLDS NUMBER : viscous forces

Draft EE 8235: Lecture 21 13 Input-output analysis body forcing velocity fluctuations fluctuations ✲ Equations of motion t ✲ ✲ Constitutive equations ✛ t ✛ polymer stress fluctuations     d 1 u amplification d 2 v − − − − − − − − − − − →     d 3 w � �� � � �� � v d • I NSIGHT INTO AMPLIFICATION MECHANISMS importance of streamwise elongated structures Hoda, Jovanovi´ c, Kumar, J. Fluid Mech. ’08, ’09 Jovanovi´ c & Kumar, JNNFM ’11

Draft EE 8235: Lecture 21 14 Inertialess channel flow: worst case amplification • No single constitutive equation can describe the range of phenomena ⋆ important to quantify influence of modeling imperfections on dynamics ω σ 2 G ( k x , k z ) = sup max ( T ( k x , k z , ω )) : We = 10 , β = 0 . 5 , Re = 0

Draft EE 8235: Lecture 21 15 G ( k x , k z ) : We = 50 , β = 0 . 5 , Re = 0

Draft EE 8235: Lecture 21 16 G ( k x , k z ) : We = 100 , β = 0 . 5 , Re = 0 • Dominance of streamwise elongated structures streamwise streaks!

Draft EE 8235: Lecture 21 17 Amplification mechanism • Highest amplification: ( d 2 , d 3 ) → u I NERTIALESS VISCOELASTIC : ‘glorified polymer viscous diffusion’ stretching dissipation normal/spanwise streamwise forcing velocity − 1 ✲ − (1 − β ) j ωβ + 1 A − 1 j ωβ + 1 ∆ − 1 ✲ We A cp2 ✲ ✲ ✲ os I NERTIAL N EWTONIAN : ‘glorified vortex viscous diffusion’ tilting dissipation normal/spanwise streamwise forcing velocity ✲ ReA cp1 (j ωI − A os ) − 1 (j ωI − ∆) − 1 ✲ ✲ ✲ ✲

Draft EE 8235: Lecture 21 18 Inertialess lift-up mechanism ∆ η t = − (1 /β )∆ η + We (1 − 1 /β ) A cp2 ϑ � � ∂ yz ( U ′ ( y ) τ 22 ) + ∂ zz ( U ′ ( y ) τ 23 ) = − (1 /β )∆ η + We (1 − 1 /β )

Draft EE 8235: Lecture 21 19 Spatial frequency responses amplification ( d 2 , d 3 ) → u − − − − − − − − − − − G ( k z ; Re ) = Re 2 f ( k z ) I NERTIAL N EWTONIAN : G ( k z ; We, β ) = We 2 g ( k z ) (1 − β ) 2 I NERTIALESS VISCOELASTIC : vortex tilting: f ( k z ) polymer stretching: g ( k z )

Draft EE 8235: Lecture 21 20 Dominant flow patterns • F REQUENCY RESPONSE PEAKS ☞ streamwise vortices and streaks Inertial Newtonian: Inertialess viscoelastic: � color plots: streamwise velocity • C HANNEL CROSS - SECTION VIEW : contour lines: stream-function

Draft EE 8235: Lecture 21 21 Flow sensitivity vs. nonlinearity • Challenge: relative roles of flow sensitivity and nonlinearity • Newtonian fluids: self-sustaining process for transition to turbulence Waleffe, Phys. Fluids ’97 Streaks O(1) advection of instability of mean shear U(y,z) Streamwise Streak wave Rolls mode (3D) O(1/R) O(1/R) nonlinear self−interaction