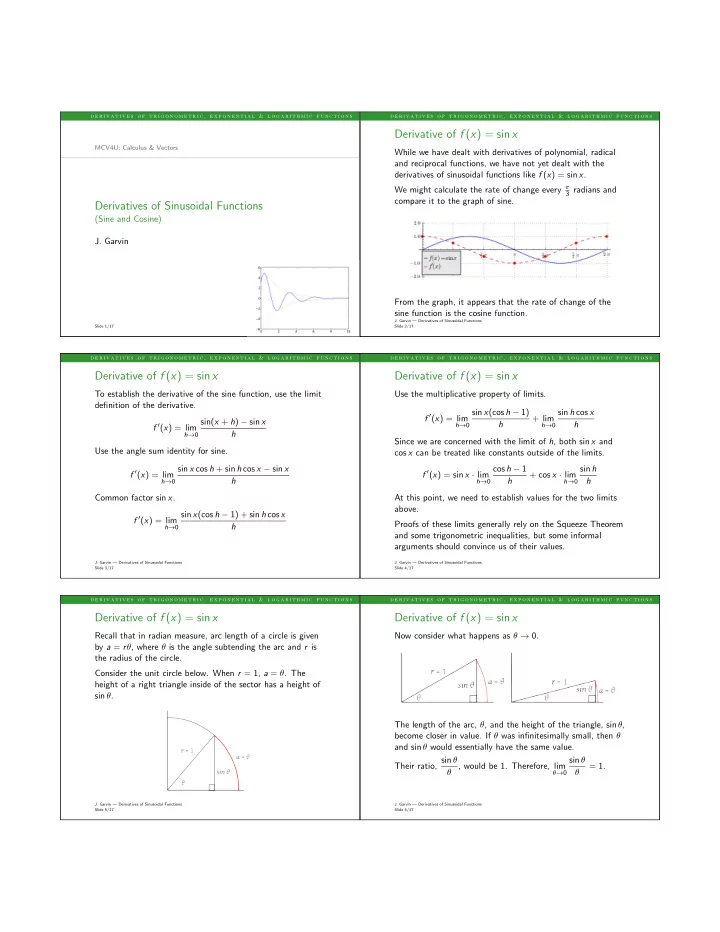
Derivative of f ( x ) = sin x MCV4U: Calculus & Vectors While - PDF document

d e r i v a t i v e s o f t r i g o n o m e t r i c , e x p o n e n t i a l & l o g a r i t h m i c f u n c t i o n s d e r i v a t i v e s o f t r i g o n o m e t r i c , e x p o n e n t i a l & l o g a r i t h m i c f u n c t i o n s Derivative of f ( x ) = sin x MCV4U: Calculus & Vectors While we have dealt with derivatives of polynomial, radical and reciprocal functions, we have not yet dealt with the derivatives of sinusoidal functions like f ( x ) = sin x . We might calculate the rate of change every π 3 radians and compare it to the graph of sine. Derivatives of Sinusoidal Functions (Sine and Cosine) J. Garvin From the graph, it appears that the rate of change of the sine function is the cosine function. J. Garvin — Derivatives of Sinusoidal Functions Slide 1/17 Slide 2/17 d e r i v a t i v e s o f t r i g o n o m e t r i c , e x p o n e n t i a l & l o g a r i t h m i c f u n c t i o n s d e r i v a t i v e s o f t r i g o n o m e t r i c , e x p o n e n t i a l & l o g a r i t h m i c f u n c t i o n s Derivative of f ( x ) = sin x Derivative of f ( x ) = sin x To establish the derivative of the sine function, use the limit Use the multiplicative property of limits. definition of the derivative. sin x (cos h − 1) sin h cos x f ′ ( x ) = lim + lim sin( x + h ) − sin x h h h → 0 h → 0 f ′ ( x ) = lim h h → 0 Since we are concerned with the limit of h , both sin x and Use the angle sum identity for sine. cos x can be treated like constants outside of the limits. sin x cos h + sin h cos x − sin x cos h − 1 sin h f ′ ( x ) = lim f ′ ( x ) = sin x · lim + cos x · lim h h h h → 0 h → 0 h → 0 Common factor sin x . At this point, we need to establish values for the two limits above. sin x (cos h − 1) + sin h cos x f ′ ( x ) = lim Proofs of these limits generally rely on the Squeeze Theorem h h → 0 and some trigonometric inequalities, but some informal arguments should convince us of their values. J. Garvin — Derivatives of Sinusoidal Functions J. Garvin — Derivatives of Sinusoidal Functions Slide 3/17 Slide 4/17 d e r i v a t i v e s o f t r i g o n o m e t r i c , e x p o n e n t i a l & l o g a r i t h m i c f u n c t i o n s d e r i v a t i v e s o f t r i g o n o m e t r i c , e x p o n e n t i a l & l o g a r i t h m i c f u n c t i o n s Derivative of f ( x ) = sin x Derivative of f ( x ) = sin x Recall that in radian measure, arc length of a circle is given Now consider what happens as θ → 0. by a = r θ , where θ is the angle subtending the arc and r is the radius of the circle. Consider the unit circle below. When r = 1, a = θ . The height of a right triangle inside of the sector has a height of sin θ . The length of the arc, θ , and the height of the triangle, sin θ , become closer in value. If θ was infinitesimally small, then θ and sin θ would essentially have the same value. Their ratio, sin θ sin θ θ , would be 1. Therefore, lim = 1. θ θ → 0 J. Garvin — Derivatives of Sinusoidal Functions J. Garvin — Derivatives of Sinusoidal Functions Slide 5/17 Slide 6/17

d e r i v a t i v e s o f t r i g o n o m e t r i c , e x p o n e n t i a l & l o g a r i t h m i c f u n c t i o n s d e r i v a t i v e s o f t r i g o n o m e t r i c , e x p o n e n t i a l & l o g a r i t h m i c f u n c t i o n s Derivative of f ( x ) = sin x Derivative of f ( x ) = sin x cos θ − 1 Now return to the previous definition of the derivative of A similar argument can be used for lim . θ θ → 0 f ( x ) = sin x and substitute these values. Consider what happens to the horizontal component of a cos h − 1 sin h right triangle, cos θ , as θ → 0. f ′ ( x ) = sin x · lim + cos x · lim h h h → 0 h → 0 = sin x · 0 + cos x · 1 = cos x This confirms our graph earlier. Derivative of the Sine Function If f ( x ) = sin x , then f ′ ( x ) = cos x . If θ was infinitesimally small, then cos θ would essentially have the same length as the radius, 1. cos θ − 1 Therefore, cos θ − 1 = 1 − 1 = 0, and lim = 0. θ θ → 0 J. Garvin — Derivatives of Sinusoidal Functions J. Garvin — Derivatives of Sinusoidal Functions Slide 7/17 Slide 8/17 d e r i v a t i v e s o f t r i g o n o m e t r i c , e x p o n e n t i a l & l o g a r i t h m i c f u n c t i o n s d e r i v a t i v e s o f t r i g o n o m e t r i c , e x p o n e n t i a l & l o g a r i t h m i c f u n c t i o n s Derivative of f ( x ) = cos x Derivatives Involving Sinusoidal Functions Use the same process for the derivative of f ( x ) = cos x . We can use the derivative rules developed earlier to find the derivatives of functions involving either sine or cosine. cos( x + h ) − cos x f ′ ( x ) = lim Example h h → 0 cos x cos h − sin x sin h − cos x Determine the derivative of f ( x ) = 10 cos x + 4. = lim h h → 0 cos x (cos h − 1) − sin x sin h Since 10 is a constant multiple, and 4 is a constant, = lim h f ′ ( x ) = − 10 sin x . h → 0 cos h − 1 sin h = cos x lim − sin x lim Example h h h → 0 h → 0 Determine the derivative of f ( x ) = sin x − cos x . = cos x · 0 − sin x · 1 = − sin x Using the difference rule for derivatives, Derivative of the Cosine Function f ′ ( x ) = cos x − ( − sin x ) = cos x + sin x . If f ( x ) = cos x , then f ′ ( x ) = − sin x . J. Garvin — Derivatives of Sinusoidal Functions J. Garvin — Derivatives of Sinusoidal Functions Slide 9/17 Slide 10/17 d e r i v a t i v e s o f t r i g o n o m e t r i c , e x p o n e n t i a l & l o g a r i t h m i c f u n c t i o n s d e r i v a t i v e s o f t r i g o n o m e t r i c , e x p o n e n t i a l & l o g a r i t h m i c f u n c t i o n s Derivatives Involving Sinusoidal Functions Derivatives Involving Sinusoidal Functions Example Example Determine the derivative of y = cos(2 x 3 + 5 x ). Determine the derivative of y = 2 sin x cos x . Use the chain rule, where the inner function is u = 2 x 3 + 5 x Use the product rule to differentiate. and the outer function is y = cos u . dy dx = 2(cos x cos x − sin x sin x ) dx = − sin(2 x 3 + 5 x )(6 x 2 + 5) dy = 2(cos 2 x − sin 2 x ) = 2 cos 2 x Example An alternative solution uses the chain rule and the identity Determine the derivative of y = 7 sin 3 x + 2 cos 2 x . y = 2 sin x cos x = sin 2 x . Use the chain rule and the fact that sin n x = (sin x ) n . dy dx = cos(2 x )(2) dy dx = 21(sin x ) 2 (cos x ) + 4(cos x )( − sin x ) = 2 cos 2 x = 21 sin 2 x cos x − 4 sin x cos x J. Garvin — Derivatives of Sinusoidal Functions J. Garvin — Derivatives of Sinusoidal Functions Slide 11/17 Slide 12/17

d e r i v a t i v e s o f t r i g o n o m e t r i c , e x p o n e n t i a l & l o g a r i t h m i c f u n c t i o n s d e r i v a t i v e s o f t r i g o n o m e t r i c , e x p o n e n t i a l & l o g a r i t h m i c f u n c t i o n s Derivatives Involving Sinusoidal Functions Derivatives Involving Sinusoidal Functions Example Example Find any values of x for which the tangent to y = 3 sin 2 x , on Determine the slope of the tangent to f ( x ) = 2 x cos x when x = 5 π 3 . the domain [0 , 2 π ], has a slope of 3 2 . Use the product rule to differentiate. Using the chain rule, the derivative is dy dx = 6 sin x cos x , or dy dx = 3 sin 2 x after applying the double-angle formula. f ′ ( x ) = 2 cos x + 2 x ( − sin x ) Set dy dx = 3 2 and solve for 2 x . = 2(cos x − x sin x ) Find f ′ � 5 π 3 sin 2 x = 3 � for the slope of the tangent. 2 3 sin 2 x = 1 f ′ � 5 π √ 2 � � �� � 2 − 5 π 1 3 2 x = sin − 1 � 1 = 2 − � 3 3 2 2 √ 2 x = π = 1 + 5 3 π 3 6 J. Garvin — Derivatives of Sinusoidal Functions J. Garvin — Derivatives of Sinusoidal Functions Slide 13/17 Slide 14/17 d e r i v a t i v e s o f t r i g o n o m e t r i c , e x p o n e n t i a l & l o g a r i t h m i c f u n c t i o n s d e r i v a t i v e s o f t r i g o n o m e t r i c , e x p o n e n t i a l & l o g a r i t h m i c f u n c t i o n s Derivatives Involving Sinusoidal Functions Derivatives Involving Sinusoidal Functions A graph of y and dy Since sin 2 x has a period of π , two cycles will be completed dx is below. on the interval [0 , 2 π ]. Thus, there should be four values of x for which this equation is true. The first two can be found by using 2 x as the reference angle. 2 x = π π − 2 x = π 6 6 x = π − π x = π 6 12 2 = 5 π 12 Find the other two by adding the period, π , to each value. x = π + π x = π + 5 π 12 12 = 13 π = 17 π 12 12 J. Garvin — Derivatives of Sinusoidal Functions J. Garvin — Derivatives of Sinusoidal Functions Slide 15/17 Slide 16/17 d e r i v a t i v e s o f t r i g o n o m e t r i c , e x p o n e n t i a l & l o g a r i t h m i c f u n c t i o n s Questions? J. Garvin — Derivatives of Sinusoidal Functions Slide 17/17