CS411 Whats the purpose of main memory buffer? Database Systems - PDF document

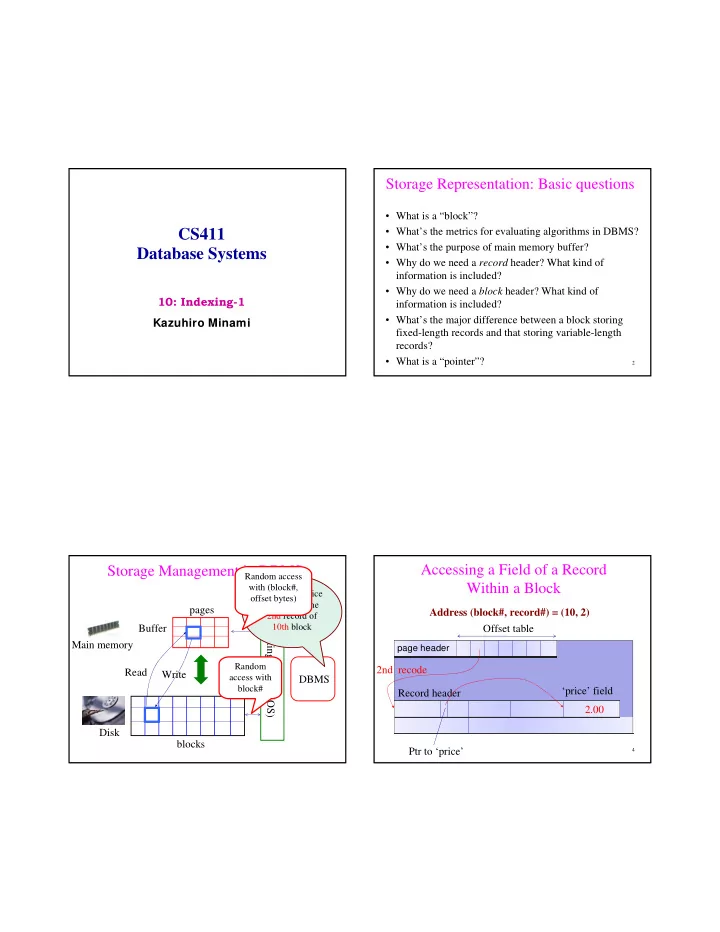
Storage Representation: Basic questions • What is a “block”? • What’s the metrics for evaluating algorithms in DBMS? CS411 • What’s the purpose of main memory buffer? Database Systems • Why do we need a record header? What kind of information is included? • Why do we need a block header? What kind of 10: Indexing-1 information is included? • What’s the major difference between a block storing Kazuhiro Minami fixed-length records and that storing variable-length records? • What is a “pointer”? 2 Accessing a Field of a Record Storage Management in DBMS Random access Within a Block with (block#, Update the price offset bytes) to $2.00 in the pages Address (block#, record#) = (10, 2) 2nd record of Operating System (OS) 10th block Buffer Offset table Main memory page page header Random 2nd recode Read Write access with DBMS block# ‘price’ field Record header 2.00 Disk blocks Ptr to ‘price’ 4

What if a user say “Update the price of Bud in Beers to $2.00”? How can we figure pages out (block#, Operating System (OS) record#)? Buffer Indexing Main memory DBMS Disk blocks How to find boxes containing “History of Probably, what you want is a table (i.e., Japan” Volume 1 – 100 from Storage? index) You can only I don’t want to Book title Box ID check out 5 boxes Q: do you think that we open all the History of Japan vol. 1 925 and takes a few solved the problem? boxes; it takes History of Japan vol. 2 925 days for delivery Q: how do you find the forever… History of Japan vol. 3 926 entry for “History of Japan” in this table? History of Japan vol. 4 928 Q: What if this table is so History of Japan vol. 5 928 big and is stored in boxes History of Japan vol. 6 928 in the storage? History of Japan vol. 7 1001 History of Japan vol. 8 1002 Librarian History of Japan vol. 9 1002 This is the exact Suppose that History of Japan vol. 10 1003 Storage with problem we Q: What kind of each box has a need to address millions of ID and boxes are information would like to in DBMS have? sorted by IDs boxes 7 8

How to first find boxes containing Index Indexes are used to speed up for “History of Japan” from Storage? selections on particular attributes Boxes Need to retrieve Search key field(s) : index blocks first for index – The attribute(s) that you want to look up tuples by – any subset of the fields of a relation – Search key is not the same as key (minimal set of fields that uniquely identify a record in a relation). Index entries take the form (k, r) Librarian Storage with record, or record millions of ID, or record IDs Search key boxes 9 There are several different kinds of Dense Indexes on a Sequential Data File indexes used in DBMSs • (key, pointer) pair for every record • File is sorted by the primary key • Clustered/unclustered – Clustered = records sorted in the (search) key order Key (key, pointer) – Unclustered = no 10 10 20 20 • Dense/sparse 30 Index 30 40 – Dense = each record has an entry in the index Data 40 blocks 50 – Sparse = only some records have blocks 60 50 70 • Primary/secondary 60 80 Keys and – Primary = on the primary key Index file 70 pointers take 80 – Secondary = on any key much less Sequential file (data file) space

Sparse Indexes on a Sequential Data File Unclustered Indexes • To index other attributes than primary key • Sparse index: one key per data block • Always dense (why ?) • Use less space, but takes more time for search • Only work with sequential files 20 10 10 10 10 30 30 20 20 50 30 20 30 70 20 40 20 90 30 10 110 50 30 130 20 60 30 150 Search the sparse 10 70 index for the 30 80 largest key less than or equal to K Sequential file (data file) How to find an index entry efficiently? 10 20 30 40 10 50 50 60 B-Trees 90 70 130 80 Data 90 file 100 170 110 120 130 140 Second-level 150 160 sparse index Index 170 180 blocks 190 200

B-Trees B-Trees: Balanced Trees • Automatically maintain as many level of index as is appropriate for the size of the file being • Intuition: indexed – Give up on sequentiality of index • Organize its blocks into a tree – Try to get “balance” by dynamic reorganization – Balanced: all paths from the root to a leaf have the same length • B+trees: • Manage the space on the blocks they use so that – Textbook refers to B+trees (a popular variant) as B-trees (as most people do) every block is between half used and completely – Distinction will be clear later (ok to confuse now) full. – No overflow blocks are needed B-Trees Basics UIUC (Alumni) Contribution! • Parameter d = the degree (In the textbook, d/2 is the parameter n ) Prof. Rudolf Bayer • Each node has k keys and k+1 pointers Rudolf Bayer studied Mathematics in Munich and at the University of Illinois, where d <= k <= 2d keys (except root) where he received his Ph.D. in 1966. After working at Boeing Research Labs he became an Associate Professor at Purdue University. He is a Professor of 30 120 240 Disk block Informatics at the Technische Universität München since 1972 and … … The 2001 SIGMOD Innovations Award goes to Prof. Rudolf Bayer of the Technical University of Munich, for his invention of the B-Tree (with Edward Keys k < 30 Keys 30<=k<120 Keys 120<=k<240 Keys 240<=k M. McCreight), of B-Tree prefix compression, and of lock coupling (a.k.a. crabbing) for concurrent access to B-Trees (with Mario Schkolnick). All of • Each leaf has k keys where d <= k <= 2d: these techniques are widely used in commercial database products. …… The Original Publication Disk block 40 50 60 Rudolf Bayer, Edward M. McCreight: Organization and Maintenance of Next leaf Large Ordered Indices. Acta Informatica 1: 173-189(1972) 40 50 60

B-Tree Example B-Tree Design Ok for the d = 2 root to have • How large d ? only one key 80 • Example: – Key size = 4 bytes 20 60 100 120 140 – Pointer size = 8 bytes – Block size = 4096 byes 10 15 18 20 30 40 50 60 65 80 85 90 • 2d * 4 + (2d+1) * 8 <= 4096 • d = 170 10 15 18 20 30 40 50 60 65 80 85 90 Searching a B-Tree Example: Find a record with key 30 • Exact key values: Only 4 blocks – Start at the root read necessary 80 – Proceed down, to the leaf Select name 20 60 100 120 140 From people • Range queries: Where age = 25 – As above 10 15 18 20 30 40 50 60 65 80 85 90 – Then sequential traversal Select name From people of the leaf nodes Where 20 <= age and age <= 30 10 15 18 20 30 40 50 60 65 80 85 90

Insertion in a B-Tree B-Trees in Practice • Typical order: 100. Typical fill-factor: 67%. Insert (K, P) – average fanout = 133 • Find leaf where K belongs, insert Big enough • Typical capacities: • If no overflow (2d keys or less), halt for most – Height 4: 133 4 = 312,900,700 records applications • If overflow (2d+1 keys), split node, insert in parent: – Height 3: 133 3 = 2,352,637 records (K3, ) to parent • Can often hold top levels in buffer pool: – Level 1 = 1 page = 8 Kbytes K1 K2 K3 K4 K5 K1 K2 K4 K5 – Level 2 = 133 pages = 1 Mbyte P0 P1 P2 P3 P4 p5 P0 P1 P2 P3 P4 p5 – Level 3 = 17,689 pages = 133 MBytes • If leaf, keep K3 too in right node Insertion in a B-Tree Insertion in a B-Tree Insert K=19 After insertion 80 80 20 60 100 120 140 20 60 100 120 140 10 15 18 20 30 40 50 60 65 80 85 90 10 15 18 19 20 30 40 50 60 65 80 85 90 10 15 18 20 30 40 50 60 65 80 85 90 10 15 18 19 20 30 40 50 60 65 80 85 90

Insertion in a B-Tree Insertion in a B-Tree Now insert 25 After insertion 80 80 20 60 100 120 140 20 60 100 120 140 10 15 18 19 20 30 40 50 60 65 80 85 90 10 15 18 19 20 25 30 40 50 60 65 80 85 90 10 15 18 19 20 30 40 50 60 65 80 85 90 10 15 18 19 20 25 30 40 50 60 65 80 85 90 Insertion in a B-Tree Insertion in a B-Tree But now have to split ! After the split 80 80 20 60 100 120 140 20 30 60 100 120 140 10 15 18 19 20 25 30 40 50 60 65 80 85 90 10 15 18 19 20 25 30 40 50 60 65 80 85 90 10 15 18 19 20 25 30 40 50 60 65 80 85 90 10 15 18 19 20 25 30 40 50 60 65 80 85 90

Deletion from a B-Tree Deletion from a B-Tree Delete 30 After deleting 30 80 80 May change to 40, or not 20 30 60 100 120 140 20 30 60 100 120 140 10 15 18 19 20 25 30 40 50 60 65 80 85 90 10 15 18 19 20 25 40 50 60 65 80 85 90 10 15 18 19 20 25 30 40 50 60 65 80 85 90 10 15 18 19 20 25 40 50 60 65 80 85 90 Deletion from a B-Tree Deletion from a B-Tree Now delete 25 After deleting 25 Need to rebalance 80 80 Rotate 20 30 60 100 120 140 20 30 60 100 120 140 10 15 18 19 20 25 40 50 60 65 80 85 90 10 15 18 19 20 40 50 60 65 80 85 90 10 15 18 19 20 25 40 50 60 65 80 85 90 10 15 18 19 20 40 50 60 65 80 85 90