cs 225
play

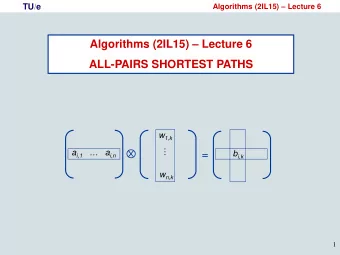
CS 225 Data Structures April 23 Dijkstras Algorithm Wad ade Fag - PowerPoint PPT Presentation

Jan 21, 2024 •109 likes •296 views

CS 225 Data Structures April 23 Dijkstras Algorithm Wad ade Fag agen-Ulm lmschneid ider Partition Property Consider an arbitrary partition of the vertices on G into two subsets U and V . V U A 4 Let e be an edge of 8 2 B D

  1. CS 225 Data Structures April 23 – Dijkstra’s Algorithm Wad ade Fag agen-Ulm lmschneid ider

  2. Partition Property Consider an arbitrary partition of the vertices on G into two subsets U and V . V U A 4 Let e be an edge of 8 2 B D minimum weight across 7 e 1 2 the partition. C 5 3 9 F E Then e is part of some minimum spanning tree.

  3. Partition Property The partition property suggests an algorithm: B 15 2 C 5 A 13 17 11 5 8 10 D E 16 H 9 12 9 16 4 F G

  4. Prim’s Algorithm PrimMST(G, s): 1 2 Input: G, Graph; 3 s, vertex in G, starting vertex 4 Output: T, a minimum spanning tree (MST) of G 5 6 foreach (Vertex v : G): B 7 d[v] = +inf 15 2 8 p[v] = NULL 9 d[s] = 0 C 5 10 A 13 11 PriorityQueue Q // min distance, defined by d[v] 11 17 12 Q.buildHeap(G.vertices()) 13 Graph T // "labeled set" 8 D E 14 16 9 15 repeat n times: 12 16 Vertex m = Q.removeMin() 17 T.add(m) 18 foreach (Vertex v : neighbors of m not in T): F 19 if cost(v, m) < d[v]: 20 d[v] = cost(v, m) 21 p[v] = m 22 23 return T

  5. 6 PrimMST(G, s): Prim’s Algorithm 7 foreach (Vertex v : G): 8 d[v] = +inf 9 p[v] = NULL 10 d[s] = 0 11 12 PriorityQueue Q // min distance, defined by d[v] 13 Q.buildHeap(G.vertices()) 14 Graph T // "labeled set" 15 16 repeat n times: 17 Vertex m = Q.removeMin() 18 T.add(m) 19 foreach (Vertex v : neighbors of m not in T): 20 if cost(v, m) < d[v]: 21 d[v] = cost(v, m) 22 p[v] = m Adj. Matrix Adj. List Heap Unsorted Array

  6. Prim’s Algorithm 16 repeat n times: 17 Vertex m = Q.removeMin() 18 T.add(m) 19 foreach (Vertex v : neighbors of m not in T): 20 if cost(v, m) < d[v]: 21 d[v] = cost(v, m) 22 p[v] = m 16 repeat n times: 17 Vertex m = Q.removeMin() 18 T.add(m) 19 foreach (Vertex v : neighbors of m not in T): 20 if cost(v, m) < d[v]: 21 d[v] = cost(v, m) 22 p[v] = m

  7. 6 PrimMST(G, s): Prim’s Algorithm 7 foreach (Vertex v : G): 8 d[v] = +inf 9 p[v] = NULL Sparse Graph: 10 d[s] = 0 11 12 PriorityQueue Q // min distance, defined by d[v] 13 Q.buildHeap(G.vertices()) 14 Graph T // "labeled set" 15 16 repeat n times: Dense Graph: 17 Vertex m = Q.removeMin() 18 T.add(m) 19 foreach (Vertex v : neighbors of m not in T): 20 if cost(v, m) < d[v]: 21 d[v] = cost(v, m) 22 p[v] = m Adj. Matrix Adj. List O(n 2 + m lg(n)) O(n lg(n) + m lg(n)) Heap Unsorted O(n 2 ) O(n 2 ) Array

  8. MST Algorithm Runtime: • Prim’s Algorithm: • Kruskal’s Algorithm: O(n lg(n) + m lg(n)) O(n + m lg(n)) • What must be true about the connectivity of a graph when running an MST algorithm? • How does n and m relate?

  9. MST Algorithm Runtime: • Kruskal’s Algorithm: O(n + m lg(n)) • Prim’s Algorithm: O(n lg(n) + m lg(n))

  10. MST Algorithm Runtime: • Upper bound on MST Algorithm Runtime: O(m lg(n))

  11. Suppose I I have a new heap: Binary Heap Fibonacci Heap O( lg(n) ) O( lg(n) ) Remove Min O( lg(n) ) O(1)* Decrease Key What’s the updated running time? PrimMST(G, s): 6 foreach (Vertex v : G): 7 d[v] = +inf 8 p[v] = NULL 9 d[s] = 0 10 11 PriorityQueue Q // min distance, defined by d[v] 12 Q.buildHeap(G.vertices()) 13 Graph T // "labeled set" 14 15 repeat n times: 16 Vertex m = Q.removeMin() 17 T.add(m) 18 foreach (Vertex v : neighbors of m not in T): 19 if cost(v, m) < d[v]: 20 d[v] = cost(v, m) 21 p[v] = m

  12. End of f Semester Logistics Lab: Your final CS 225 lab is this week. • No lab sections next week (partial week) . Final Exam: Final exams start on Reading Day (May 3) • Last day of office hours is Wednesday, May 2. • No office/lab hours once the first final exam is given. Grades: There will be a “Pre - Final” grade update posted next week with all grades except your final. • MP7’s grace period extends until Tuesday, May 1 • Goal: Have “Pre - Final” grade on Wednesday/Thursday

  13. Shortest Path

  15. Dijkstra’s Algorithm (SSSP) DijkstraSSSP(G, s): 6 foreach (Vertex v : G): 7 d[v] = +inf 8 p[v] = NULL 9 d[s] = 0 10 11 PriorityQueue Q // min distance, defined by d[v] 12 Q.buildHeap(G.vertices()) 13 Graph T // "labeled set" 14 7 B 15 repeat n times: 10 C 16 Vertex u = Q.removeMin() A 17 T.add(u) 5 18 foreach (Vertex v : neighbors of u not in T): 6 4 3 D 19 if _______________ < d[v]: 3 20 d[v] = __________________ E 7 21 p[v] = m H 5 2 5 4 F G

  16. Dijkstra’s Algorithm (SSSP) What about negative weight cycles? 7 B 10 C A 5 -6 4 3 D 3 E 7 H 5 2 -5 4 F G

  17. Dijkstra’s Algorithm (SSSP) What about negative weight edges, without negative weight cycles? 7 B 10 C A 5 6 4 3 D 3 E 7 H 2 -2 5 3 F G

  18. Dijkstra’s Algorithm (SSSP) What is the running time? DijkstraSSSP(G, s): 6 foreach (Vertex v : G): 7 d[v] = +inf 8 p[v] = NULL 9 d[s] = 0 10 11 PriorityQueue Q // min distance, defined by d[v] 12 Q.buildHeap(G.vertices()) 13 Graph T // "labeled set" 14 15 repeat n times: 16 Vertex u = Q.removeMin() 17 T.add(u) 18 foreach (Vertex v : neighbors of u not in T): 19 if _______________ < d[v]: 20 d[v] = __________________ 21 p[v] = m

Recommend

More recommend