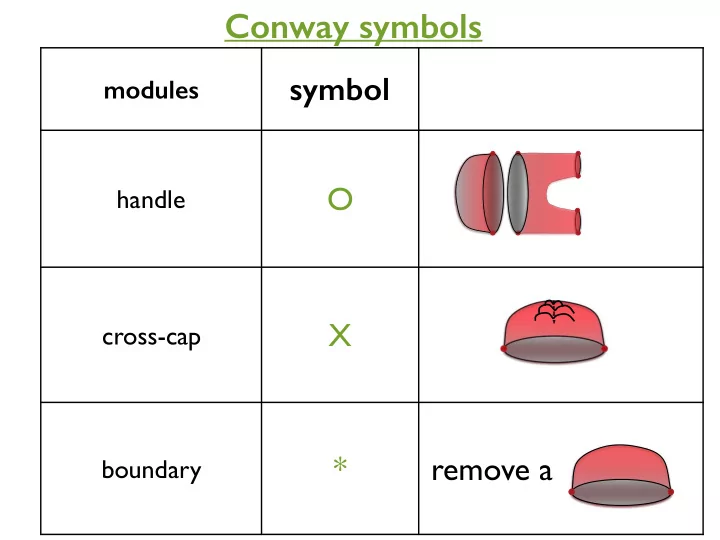

Conway symbols symbol modules O handle X cross-cap * remove a boundary
here are some manifolds / orbifolds: torus cylinder Moebius strip Klein bottle
what are these manifolds? cylinder Moebius strip to here torus Klein bottle
which ones are nice (oriented), nasty? cylinder Moebius strip torus Klein bottle
how many caps? xcaps? handles? boundaries? TWO boundaries ONE boundary ONE crosscap cylinder Moebius strip ONE handle TWO crosscaps torus Klein bottle
what are their Conway symbols? TWO boundaries ONE boundary * * * x ONE crosscap cylinder Moebius strip o xx ONE handle TWO crosscaps torus Klein bottle
what is their geometry? * * * x cylinder Moebius strip euclidean, K=0 o xx torus Klein bottle
what is their geometry? * * * x cylinder Moebius strip o xx torus Klein bottle
Let’s build the universal cover of these manifolds… * * * x The universal covers tile cylinder Moebius strip the euclidean plane, E^2 o xx torus Klein bottle
covers and universal cover of manifolds “ Classical Topology and Combinatorial Group Theory ” John Stillwell
build the “universal cover” of o: cover 4 4 4 4 universal cover - E2 tiled by (4,4)
build the “universal cover” of oo: 8 universal cover - H2 tiled by (8,8)!
Conway symbols describe “orbifolds” Orbifolds describe symmetric patterns
All these manifolds print to euclidean plane! • o • ** • xx • *x
Zipping and unzipping manifolds is a good way to explore topology (and, symmetry…)
* * * x cylinder Moebius strip o xx torus Klein bottle
The torus prints a 2-periodic pattern in the euclidean plane, with symmetry p1!
Klein bottle prints a pair of glide lines ( xx = pg)
Annulus prints a pair of mirrors.. boundaries/punctures (*) print mirror lines ( ** = pm)
generic 2D symmetries include: 1. reflections (e.g. p3m1) 2. glides (e.g. cm) 3.translations (e.g. p1) 4. rotations (e.g. p3)
a cone-point prints a rotation centre (e.g. 5 point)
a cone-point prints a rotation centre Conway, Goodman-Strauss and Burgiel (e.g. 3 point)
e.g. 4 order-2 cone points: print orbifold universal cover (eucl. plane) Conway, Goodman-Strauss and Burgiel orbifold universal cover (eucl. plane) glue 2222
e.g. 2 order-2 cone points + puncture: glue universal cover orbifold Conway, Goodman-Strauss and Burgiel universal cover orbifold print 22*
intersecting mirrors = corner points Conway, Goodman-Strauss and Burgiel 3*3
adding cone-points, corner-points to manifolds: ORBIFOLDS
generic 2D symmetries include: 1. reflections (e.g. p3m1) punctures 2. glides (e.g. cm) crosscaps 3.translations (e.g. p1) handles 4. rotations (e.g. p3) ???
Orbifold = orbit manifold (Thurston) symbol modules O handle X cross-cap * remove a mirror boundary i cone point *j corner point
Orbifolds encode isometries into • manifold singularities (cones, corners) • topological features: 1. rotations centres induce cones 2. rotations on intersecting mirrors induce corners 3. mirror lines induce punctures 4. glide reflections (not on mirrors) induce xcaps 6. translations (not induced by other isometries) induce handles
Dissecting an Orbifold Symbol oo.. 34.. *345 * *..xx Handles Punctures with corners Cone Points Cross Caps NOTICE THAT o , *, x are TOPOLOGICAL FEATURES
ANY manifold= sphere + handles + xcaps + boundary! what is the equivalent index for an orbifold?
ANY orbifold is a manifold plus singular conformal structures : sphere + handles + xcaps + boundaries + cones + corners! what is for an orbifold?
The Orbifold Dictionary includes any combination of characters except : AB, *ab, where A ≠ B and a ≠ b oo.. 34.. *345 * *x
oo.. 34.. *345 * *..xx Handles Mirror Strings Cone Points Cross Caps What is the characteristic of this orbifold?
oo 34*345 * * x x x 2-(2+2+2/3+3/4+1+2/6+3/8+4/10+1+1+1+1+1) = -1263/120 characteristic is negative, so hyperbolic…..
flat orbifolds: any allowed orbifold word with is a wallpaper group! elliptic orbifolds: any allowed orbifold word with is a point group!
the most interesting orbifolds are HYPERBOLIC S.T. Hyde, S.J. Ramsden and V. Robins, “Unification and classification of 2D crystalline patterns using orbifolds”, Acta Cryst A70, 319–337 (2014)
Like the euclidean plane... the hyperbolic plane has many possible symmetry types e.g. rotational symmetry
flat (K=0)
elliptic (K>0) hyperbolic (K<0)
Orbifold dictionary has only 3 dialects: Elliptic Euclidean Hyperbolic
Orbifold dictionary has only 3 dialects: but, nearly all words are hyperbolic!
There are many many 2D orbifolds (far more than wallpaper or point groups!) Need a classification Sort via • simply vs. multiply connected • nice vs. nasty • bounded vs. unbounded • added corners / cones Conway Symbols Have Pretty Much All Topologies
• simply connected C H S P T M • multiply connected A
coxeter
KALEIDOTILE
stellate
hat
Any orbifold whose Euler characteristic is a euclidean isometry orbifold feature Euler characteristic sphere (Identity) 2 ( 1 ) handle (translation) -2 o puncture (mirror) -1 * cross-cap (glide) -1 x cone (rotation) A corner (mirror + rot’n) *k
euclidean orbifolds = wallpaper groups
orbifold feature Euler characteristic sphere (Identity) 2 ( 1 ) handle (translation) -2 o puncture (mirror) -1 * cross-cap (glide) -1 x cone (rotation) A corner (mirror + rot’n) *k
orbifold gives simple group-subgp information: Traditional description Orbifold description *235 235 *234 234 3*2 *233 233
cost 1/60 *235 1/30 235 1/24 *234 1/12 234 3*2 *233 1/6 233 group order = 2/ index subgroup (H) in group (G) = (H)/ (G)
Any orbifold whose Euler characteristic is negative will print a pattern in the hyperbolic plane orbifold feature Euler characteristic sphere (Identity) 2 ( 1 ) handle (translation) -2 o puncture (mirror) -1 * cross-cap (glide) -1 x cone (rotation) A corner (mirror + rot’n) *k since any combination of these characters is an allowed orbifold (except *ik and AB where i ≠ j and A ≠ B ) nearly all 2D symmetries are hyperbolic!
possible “orbifolds” on the hyperbolic plane *237, *245, *334, *2223 mirrors 3*4, 4*3, 32*, 3*22 mirrors and rotations 239, 24(12), 33(35), 2229 rotations (cone points) 79x glides (cross-caps) (+ corners) *2* non-intersecting mirrors 6*89x cross-caps and mirrors ooooooooooo translations xxxxx multiple cross-caps 61
Rank orbifolds by area of orbifold - from most to least symmetric
Generic hyperbolic orbifolds do not map into 3D euclidean space to form discrete symmetry groups…. …. but many do! AND the most symmetric examples build 2- and 3-periodic crystalline hyperbolic surfaces!
Only some hyperbolic orbifolds map to 3D flat space... The smallest hyperbolic orbifold The smallest orbifold that “fits” 3D euclidean space (?)
So this is the smallest homogeneous hyperbolic grain size allowed in 3d space! *246 symmetry
P surface is a 2d tiling of 246 triangles in H^2
P-Surface: *246 orbifold coxeter orbifold (cf. *333, *235)
H^2 and P, D, Gyroid all share *246 2d hyperbolic symmetry H yperbolic plane P Gyroid D
These Triply Periodic Minimal Surfaces are likely the “least frustrated” embeddings of 2d hyperbolic space in 3d euclidean space! Known to be the most symmetric three-periodic surfaces:
Gyroid is everywhere in materials science and biology…. M. Evans • see Angew. Chemie Int. Ed ., 47, 7996-8000 (2008) Nature Materials , November 2008, “A twisted tale”
These hyperbolic orbifolds map to P , D, G surfaces in euclidean 3-space to give 3D space groups: 3-periodic “crystallographic hyperbolic orbifolds” via genus-3
Why bother to probe 3d euclidean space via 2d hyperbolic space? Resulting crystallographic structures can be very complex in 3d space, but emerge from very simple 2d hyperbolic patterns Hyperbolic “Penny packing” penny packings (3,6) (3,7)
The smallest (sub)orbifolds of *237 that “fit” 3D euclidean space
Ideal “unfrustrated” structure in H2 “Frustrated” structure in E3 regular (3,7) irregular (3,7)
Graphene is a euclidean 2d material 2 2’ 2’ 2” 2” 2’’’ can draw as universal cover of the 2222 euclidean orbifold
HYPERBOLIC Graphene 3 2 2’ 2’ 2’ 2” 2” 2” 2” 2’’’ 2’’’ 2222 euclidean orbifold 2223 HYPERBOLIC orbifold OR 23x HYPERBOLIC orbifold
M. Cramer Pedersen
Recommend
More recommend