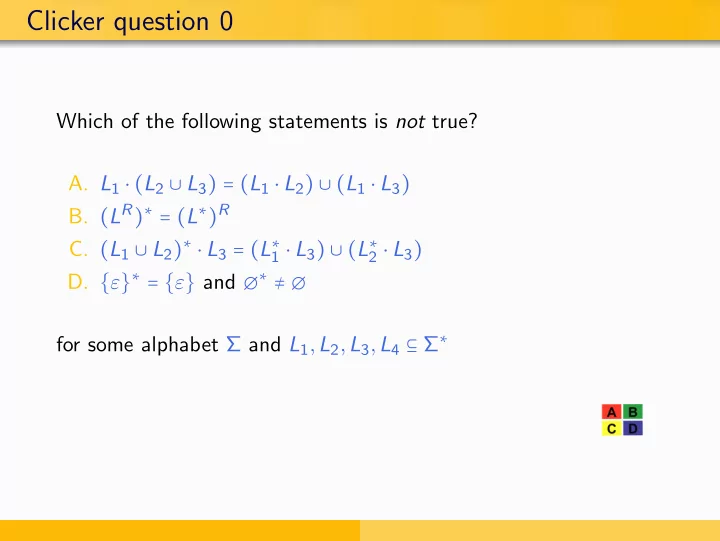
Clicker question 0 Which of the following statements is not true? A. - PowerPoint PPT Presentation

Clicker question 0 Which of the following statements is not true? A. L 1 ⋅ ( L 2 ∪ L 3 ) = ( L 1 ⋅ L 2 ) ∪ ( L 1 ⋅ L 3 ) B. ( L R ) ∗ = ( L ∗ ) R C. ( L 1 ∪ L 2 ) ∗ ⋅ L 3 = ( L ∗ 1 ⋅ L 3 ) ∪ ( L ∗ 2 ⋅ L 3 ) D. { ε } ∗ = { ε } and ∅ ∗ ≠ ∅ for some alphabet Σ and L 1 , L 2 , L 3 , L 4 ⊆ Σ ∗

A play of tennis game, set, match love, 15, 30, 40, game winning also requires at least two scores more deuce, advantage-in, advantage-out

A tennis automaton game-in s s s 40-love s s o 30-love 40-15 adv-in s s o o o s 15-love 30-15 40-30 s s s o o o love 15-all 30-all deuce s s s o o o o s love-15 15-30 30-40 s s o o love-30 15-40 adv-out s o o love-40 o o o game-out

A tennis automaton (cont.) game-in s s s 40-love s s o 30-love 40-15 adv-in s s o o 30-15 40-30 o s 15-love s s s o o o love 15-all 30-all deuce s s s o o o love-15 15-30 30-40 o s s s o o love-30 15-40 adv-out s o o love-40 o o o game-out single initial state one or more final states many labeled transitions

A tennis automaton (cont.) game-in s s s 40-love s s o 40-15 30-love adv-in s s o o 15-love 30-15 40-30 o s s s s o o o love 15-all 30-all deuce s s s o o o o s love-15 15-30 30-40 s s o o love-30 15-40 adv-out s o o love-40 o o o game-out accepted strings like sososs and soossosooo

Clicker question 1 Which string is not accepted by the tennis automaton? game-in s s s 40-love s s o 40-15 30-love adv-in s s o o o s 15-love 30-15 40-30 s s s o o o love 15-all 30-all deuce s s s o o o o s love-15 15-30 30-40 s s o o A. sossooososoo love-30 15-40 adv-out s o o love-40 B. ssssos o o o game-out C. ooosssss D. all are accepted

Deterministic Finite Automata 2IT70 Finite Automata and Process Theory Technische Universiteit Eindhoven April 23, 2014

Deterministic finite automaton DFA D = ( Q , Σ , δ, q 0 , F ) Q finite set of states Σ finite alphabet δ ∶ Q × Σ → Q transition function q 0 ∈ Q initial state F ⊆ Q set of final states 2 IT70 (2014) Section 2.1 8 / 19

The tennis example game-in s s s 40-love s s o 30-love 40-15 adv-in s s o o o s 15-love 30-15 40-30 s s s o o o love 15-all 30-all deuce s s s o o o o s love-15 15-30 30-40 s s o o 15-40 love-30 adv-out s o o love-40 o o o game-out 2 IT70 (2014) Section 2.1 9 / 19

An example DFA? game-in s s s 40-love s s o 30-love 40-15 adv-in s s o o 15-love 30-15 40-30 o s s s s o o o love 15-all 30-all deuce s s s o o o love-15 15-30 30-40 o s s s o o love-30 15-40 adv-out s o o love-40 o o o game-out set of states { love , 15–love , love–15 , ... } game-in , game-out , deuce , adv-in , adv-out } alphabet { s , o } s o � → 15–love, love � → love–15, ... transitions love initial state love set of final states { game-in , game-out } 2 IT70 (2014) Section 2.1 10 / 19

one-step and multi-step yield configuration ( q , w ) for state q and string w one-step yield ( q , w ) ⊢ D ( q ′ , w ′ ) iff ∃ a ∶ w = aw ′ , δ ( q , a ) = q ′ multi-step yield ( q , w ) ⊢ ∗ D ( q ′ , w ′ ) iff ∃ n ⩾ 0 ∃ w 0 ,... , w n ∈ Σ ∗ ∃ q 0 ,... , q n ∈ Q ∶ ( q , w ) = ( q 0 , w 0 ) , ( q i − 1 , w i − 1 ) ⊢ D ( q i , w i ) , for i = 1 .. n ( q n , w n ) = ( q ′ , w ′ ) ( q , w ) = ( q 0 , w 0 ) ⊢ D ( q 1 , w 1 ) ⊢ D ⋯ ⊢ D ( q n , w n ) = ( q ′ , w ′ ) for suitable n , w 0 ,... , w n , q 0 ,... , q n 2 IT70 (2014) Section 2.1 11 / 19

Another example DFA a , b b a a a b q 0 q 1 q 2 q 3 b ( q 0 , abaa ) ⊢ ( q 1 , baa ) ⊢ ( q 0 , aa ) ⊢ ( q 1 , a ) ⊢ ( q 2 ,ε ) ( q 0 , bbaa ) ⊢ ( q 0 , baa ) ⊢ ( q 0 , aa ) ⊢ ( q 1 , a ) ⊢ ( q 2 ,ε ) ( q 1 , aa ) ⊢ ∗ ( q 2 ,ε ) and ( q 1 , aaaa ) ⊢ ∗ ( q 2 ,ε ) ( q 0 , aab ) ⊢ ∗ ( q 3 ,ε ) , ( q 0 , baab ) ⊢ ∗ ( q 3 ,ε ) , and ( q 0 , baaaabaabb ) ⊢ ∗ ( q 3 ,ε ) 2 IT70 (2014) Section 2.1 12 / 19

Language accepted by DFA L ( D ) = { w ∈ Σ ∗ ∣ ∃ q ∈ F ∶( q 0 , w ) ⊢ ∗ D ( q ,ε )} a , b b a a a b q 0 q 1 q 2 q 3 b accepted language { w ∈ { a , b } ∗ ∣ w has a substring aab } 2 IT70 (2014) Section 2.1 13 / 19

Clicker question 2 Which language is the language accepted by the this automaton? a ee oe a b b b b a eo oo a A. { a , b , aba , bab } B. { a ( bb ) n ∣ n ⩾ 0 } ∪ { b ( aa ) n ∣ n ⩾ 0 } C. { w ∈ { a , b } ∗ ∣ # a ( w ) is odd } D. { w ∈ { a , b } ∗ ∣ # a ( w ) + # b ( w ) is odd } 2 IT70 (2014) Section 2.1 14 / 19

Path sets DFA D , state q pathset D ( q ) = { w ∈ Σ ∗ ∣ ( q 0 , w ) ⊢ ∗ D ( q ,ε )} a even odd a { a n ∣ n ⩾ 0, n even } pathset D ( even ) = { a n ∣ n ⩾ 0, n odd } pathset D ( odd ) = 2 IT70 (2014) Section 2.1 15 / 19

Yet another example DFA 0 , 1 0 1 1 q 0 q 1 q 2 0 L = { w ∈ { 0 , 1 } ∗ ∣ w has no substring 11 } state pathset regular expressions q 0 no substring 11 and no last symbol 1 0 ∗ ( 10 + ) ∗ 0 ∗ ( 10 + ) ∗ 1 q 1 no substring 11 and last symbol 1 q 2 ( 0 + 1 ) ∗ 11 ( 0 + 1 ) ∗ substring 11 regular expressions will be explained later 2 IT70 (2014) Section 2.1 16 / 19

Another example DFA (rev.) a state pathset ee oe a ee { w ∣ # a ( w ) even, # b ( w ) even } { w ∣ # a ( w ) odd, # b ( w ) even } oe b b b b eo { w ∣ # a ( w ) even, # b ( w ) odd } a eo oo { w ∣ # a ( w ) odd, # b ( w ) odd } oo a L ( D ) pathset D ( eo ) ∪ pathset D ( oe ) = { w ∣ # a ( w ) odd, # b ( w ) even } ∪ = { w ∣ # a ( w ) even, # b ( w ) odd } { w ∣ # a ( w ) + # b ( w ) odd } = { w ∣ ∣ w ∣ odd } = 2 IT70 (2014) Section 2.1 17 / 19

Language accepted by DFA (revisited) a , b b a a a b q 0 q 1 q 2 q 3 b state pathset q 0 { w ∣ no substring aa , not ending in a } q 1 { w ∣ no substring aa , ending in a } q 2 { w ∣ ending in aa } { w ∣ substring aab } q 3 accepted language { w ∈ { a , b } ∗ ∣ w has a substring aab } 2 IT70 (2014) Section 2.1 18 / 19

Clicker question 3 Why does the following not represent a DFA? 1 2 3 0 0 q 0 q 1 q 2 A. The alphabet has more than 2 letters. B. It accepts the empty string ε . C. It has a transition relation, but not a transition function. D. It does represent a DFA. 2 IT70 (2014) Section 2.1 19 / 19