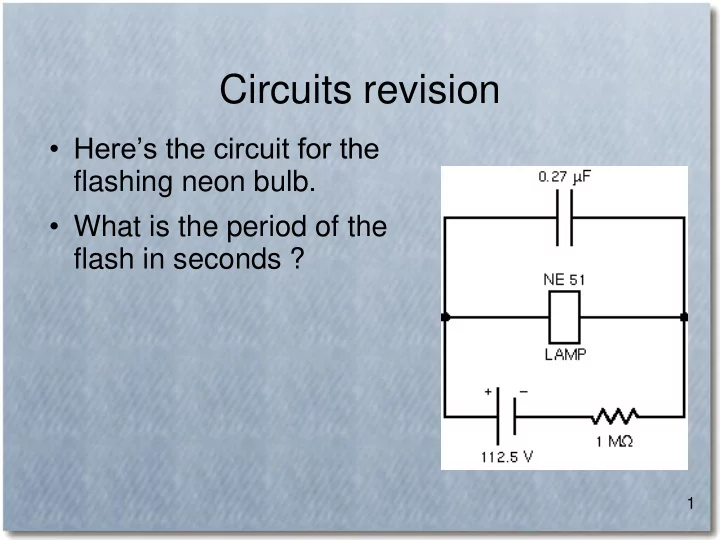
Circuits revision Heres the circuit for the flashing neon bulb. - PowerPoint PPT Presentation

Circuits revision • Here’s the circuit for the flashing neon bulb. • What is the period of the flash in seconds ? 1

Magnetic Fields revision Please try problem 15 in Ch 24 on page 825. “What is the magnetic field at the center of the loop….” 2

Magnetic Fields and Forces • Magnetism • Magnetic field shapes and direction • Fields near electric currents • Magnetic forces • Moving charges and magnetism • Magnetic machines • Magnetic materials 3

Magnetism • Fundamental force of nature • Related to electricity, but not the same 4

Experimental Observations • Magnetism does not move an electroscope, it does not act on stationary charges • Long range force (action over a distance) • There are 2 poles, north and south , and they come in pairs • Like poles repel, unlike poles attract • Poles attract magnetic materials 5

Magnetic Field lines • Magnetic Fields around a bar magnet • Similar to an electric dipole • Start at north pole, terminate at south pole 6

Like and unlike poles Magnetic field lines between poles 7

Electric Currents and Magnetic Fields Oersted found that a current can move a magnetic compass 8

Direction of Magnetic field We use the right handed rule to find which way a magnetic compass would point 9

Magnetic field near a loop • Bend the wire into a loop. • Dots - field is coming out of the page. • Crosses - field is going in to the page 10

Field near a solenoid • Many loops will concentrate the field inside the coil • Called a solenoid – contains a uniform magnetic field 11

Magnetic field due to a current Experimentally, the field strength, B, is proportional to current, I, and inversely proportional to distance, r.  I  0 B  2 r Units of Tesla, where μ 0 is the permeability constant – 1.257x10 -6 TmA -1 12

Tesla is a large unit • Magnets in the lab – 0.1 to 1 T • Kitchen magnets – 5x10 -3 T • Earths magnetic field – 5x10 -5 T • Superconducting magnets – in accelerators and maglev trains – 10 T 13

Magnetic Field at the center of a current loop Inside a loop radius R:  I  0 B 2 R 14

Magnetic Field at the center of a current loop with N turns If the loop has N turns, but its not yet a solenoid we have:  NI  0 B 2 R 15

Magnetic field inside a solenoid The uniform field in a solenoid is N   B I 0 L For a solenoid with N turns, Length L and current I. Note: independent of the coil radius. Field is uniform. 16

Magnetic Forces • The magnetic fields around two wires will attract or repel, just like bar magnets. • A magnetic field exerts a force on a current, or moving charge • Currents in the same direction attract • Opposite currents repel 17

Direction of Magnetic Force • The force on a wire with a current is perpendicular to both the magnetic field the direction of the current. • We use another right hand rule 18

Magnitude of the Magnetic Force The force between a magnetic field and a current along a wire length L perpendicular to the field is: F  ILB 19

Magnitude of the Magnetic Force The force between a magnetic field and a current along a wire length L at an angle, α to the field is: F   ILB sin If the current and B field are parallel – there is no force. 20

Force on a moving charge • A current, I, is a L  moving charge. v  • The charge q moves t along the wire length q qv L in time Δ t   I • The velocity will be  t L L/ Δ t  IL qv • We find that qv=IL 21

Magnitude of the Magnetic Force The force between a magnetic field and a charge, q, moving with a velocity, v perpendicular to the field is: F  qvB 22

Magnitude of the Magnetic Force The force between a magnetic field and a charge, q, moving at velocity, v, at an angle, α to the field is: F   qvB sin If the moving charge and B field are parallel – there is no force. 23

Direction of Magnetic Force • The force on a moving charge is perpendicular to both the magnetic field the direction of the charge. • Note the thumb is now the direction of the +ve charge, instead of the current I. 24

Path of charges in a magnetic field • The force on a charged particle in a magnetic field is perpendicular to its direction of motion. • We always get circular or spiral paths of charged paths in a magnetic field 25

Path of charges in a magnetic field • Centripetal force of an object in a circle 2 mv   F qvB r RqB   v m 26

Path of charges in a magnetic field • If we accelerated the ions in an electric field V, the charge to mass ratio can be measured, 1   2 E qV mv 2 q 2 V   2 2 m B R 27

Mass spectrometer • First measurement of e/m for the electron • Used to distinguish different types of atoms and isotopes 28

Aurora Borealis • Solar wind from the sun (protons & electrons) gets deflected by Earth’s magnetic field. • Portion of velocity perpendicular to the field lines, curves the ionizing particles into spirals • Ionize O 2 and N 2 in the ionosphere 29

Magnetic forces between currents • Consider two wires carrying currents I 1 and I 2 . • The field at the top wire  is I  0 2 B  2 2 d  F B I L 12 2 1  LI I  0 1 2 F  12 2 d 30

Magnetic forces between currents From the field from the single wire, we can deduce the force between 2 wires carrying currents I 1 and I 2 is  LI I  0 1 2 F   parallel wires 2 d 31

Torques and Magnetic Moments • Torque was defined in chapter 7 • Quantity to measure the force applied near a pivot • Useful for calculating rotational motion 32

Torque Torque, τ , measures the effectiveness of a force at causing an object to rotate about a pivot    rF sin 33

Torque on a current loop in a B field • Current loop in a uniform field • The forces on the top and bottom wires will rotate the loop 34

Torque on a current loop in a B field • The total torque, τ , will be the sum of the torques on the top and bottom wires. • Loop height L, wire length W L    2 F sin 2   BIWL sin 35

Torque on a current loop in a B field • In general, the torque on a loop area A will be:    IAB sin The loop is forced to align with the magnetic field 36

Using torque - MRIs • Magnetic Resonance Imaging (MRI) uses the protons magnetic moment in hydrogen atoms in high 1T fields. • The rate of the emitted radio waves from the excited states are detected 37

Using Torque – Electric motor Using commutators, the loop can be made to spin, to produce rotational movement 38

Permanent Magnets - Ferromagnetism • Ferromagnetism is a property of certain elements – the ability to maintain a permanent magnetic field • Depends on the crystalline structure of the metal • Found in alloys of iron, cobalt, nickel, gadolinium, dysprosium, europium • Half full electron shells, the magnetic dipole of the electrons can align 39

Periodic Table 40

Crystalline structure aligned • The magnetic dipoles are grouped in micron size crystals, domains • The dipoles can be aligned by applying a magnetic field • Can be destroyed by heating (Curie point) or dropping 41

Electromagnets • An iron core near a solenoid will align the domains inside the iron • This increases the magnetic field (factor of 100) • Used to amplify the magnetic field 42

Summary • Magnetism • Magnetic field shapes and direction • Fields near electric currents • Magnetic forces • Moving charges and magnetism • Magnetic machines • Magnetic materials 43

Homework problems Chapter 24 Problems 20, 21, 31, 41, 48, 53, 56, 57 44