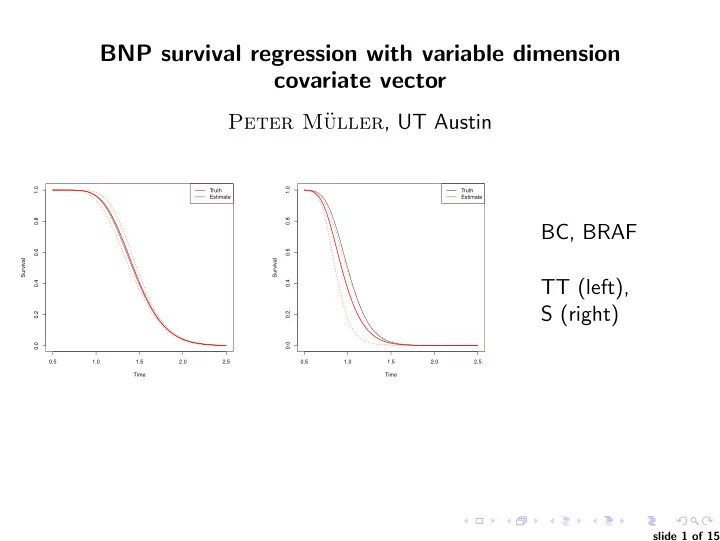

BNP survival regression with variable dimension covariate vector Peter M¨ uller , UT Austin 1.0 1.0 Truth Truth Estimate Estimate 0.8 0.8 BC, BRAF 0.6 0.6 Survival Survival TT (left), 0.4 0.4 S (right) 0.2 0.2 0.0 0.0 0.5 1.0 1.5 2.0 2.5 0.5 1.0 1.5 2.0 2.5 Time Time slide 1 of 15
BNP survival regression with variable dimension covariate vector Peter M¨ uller , UT Austin 1.0 1.0 Truth Truth Estimate Estimate 0.8 0.8 BC, BRAF 0.6 0.6 Survival Survival TT (left), 0.4 0.4 S (right) 0.2 0.2 0.0 0.0 0.5 1.0 1.5 2.0 2.5 0.5 1.0 1.5 2.0 2.5 Time Time TRT TUMOR PFS CENS MUTATIONS m1 m2 m3 m4 m5 m6 m7 m8 . . . TT THYROID 2.6 0 NA NA NA NA NA NA NA NA TT THYROID 3.6 0 NA 0 0 0 NA 0 NA NA S OVARIAN 4.2 1 0 NA 0 0 0 0 0 0 S MELANOMA 5.8 1 NA 0 0 0 NA 0 0 0 . . . . . . . . . . . . slide 1 of 15
1. Clinical Trial of Targeted Therapies w. Don Berry & Lia Tsimbouridou , M.D. Anderson, Riten Mitra , U. Louisville, Yanxun Xu , JHU, Clinical trial: study of targeted therapy (TT) vs. standard care (S) in metastatic cancers. patients with metastatic cancers (thyroid, ovarian, melano, lung, breast, CRC and other) Objective: determine whether TT leads to > progression free survival (PFS) A study for targeted therapy slide 2 of 15
1. Clinical Trial of Targeted Therapies w. Don Berry & Lia Tsimbouridou , M.D. Anderson, Riten Mitra , U. Louisville, Yanxun Xu , JHU, Clinical trial: study of targeted therapy (TT) vs. standard care (S) in metastatic cancers. patients with metastatic cancers (thyroid, ovarian, melano, lung, breast, CRC and other) Objective: determine whether TT leads to > progression free survival (PFS) Secondary objective: find subgroups for ◮ reporting of winning subgroup for future study A study for targeted therapy slide 2 of 15
1. Clinical Trial of Targeted Therapies w. Don Berry & Lia Tsimbouridou , M.D. Anderson, Riten Mitra , U. Louisville, Yanxun Xu , JHU, Clinical trial: study of targeted therapy (TT) vs. standard care (S) in metastatic cancers. patients with metastatic cancers (thyroid, ovarian, melano, lung, breast, CRC and other) Objective: determine whether TT leads to > progression free survival (PFS) Secondary objective: find subgroups for ◮ reporting of winning subgroup for future study ◮ adaptive treatment allocation A study for targeted therapy slide 2 of 15
1. Clinical Trial of Targeted Therapies w. Don Berry & Lia Tsimbouridou , M.D. Anderson, Riten Mitra , U. Louisville, Yanxun Xu , JHU, Clinical trial: study of targeted therapy (TT) vs. standard care (S) in metastatic cancers. patients with metastatic cancers (thyroid, ovarian, melano, lung, breast, CRC and other) Objective: determine whether TT leads to > progression free survival (PFS) Secondary objective: find subgroups for ◮ reporting of winning subgroup for future study ◮ adaptive treatment allocation heterogeneous pat population different mutations; different cancers; basline covs . . . Treatment might be effective in a sub-population A study for targeted therapy slide 2 of 15
2. BNP survival regression for variable dim x with F. Quintana , PUCC, Chile and Gary Rosner , JHU. Variables: for each patient i = 1 , . . . , n ◮ Outcome y i PFS; ◮ Covariates x i = ( c i , m i , b i ) ◮ tumor type c i ∈ { 1 , . . . , C } (categorical) ◮ molecular aberrations m i = ( m i 1 , . . . , m iM ) with m is = 1 for observed aberration, m is = − 1 for not observed (and 0 for n/a). ◮ other baseline covariates b i (age, # prior threrapies, etc.) Model slide 3 of 15
2. BNP survival regression for variable dim x with F. Quintana , PUCC, Chile and Gary Rosner , JHU. Variables: for each patient i = 1 , . . . , n ◮ Outcome y i PFS; ◮ Covariates x i = ( c i , m i , b i ) ◮ tumor type c i ∈ { 1 , . . . , C } (categorical) ◮ molecular aberrations m i = ( m i 1 , . . . , m iM ) with m is = 1 for observed aberration, m is = − 1 for not observed (and 0 for n/a). ◮ other baseline covariates b i (age, # prior threrapies, etc.) Challenges: prob model needs to allow for ◮ many m j are not recorded → var dimension covariate vector x i = ( m i , c i , b i ), Model slide 3 of 15
2. BNP survival regression for variable dim x with F. Quintana , PUCC, Chile and Gary Rosner , JHU. Variables: for each patient i = 1 , . . . , n ◮ Outcome y i PFS; ◮ Covariates x i = ( c i , m i , b i ) ◮ tumor type c i ∈ { 1 , . . . , C } (categorical) ◮ molecular aberrations m i = ( m i 1 , . . . , m iM ) with m is = 1 for observed aberration, m is = − 1 for not observed (and 0 for n/a). ◮ other baseline covariates b i (age, # prior threrapies, etc.) Challenges: prob model needs to allow for ◮ many m j are not recorded → var dimension covariate vector x i = ( m i , c i , b i ), ◮ extrapolation with small # obs. Model slide 3 of 15
2. BNP survival regression for variable dim x with F. Quintana , PUCC, Chile and Gary Rosner , JHU. Variables: for each patient i = 1 , . . . , n ◮ Outcome y i PFS; ◮ Covariates x i = ( c i , m i , b i ) ◮ tumor type c i ∈ { 1 , . . . , C } (categorical) ◮ molecular aberrations m i = ( m i 1 , . . . , m iM ) with m is = 1 for observed aberration, m is = − 1 for not observed (and 0 for n/a). ◮ other baseline covariates b i (age, # prior threrapies, etc.) Challenges: prob model needs to allow for ◮ many m j are not recorded → var dimension covariate vector x i = ( m i , c i , b i ), ◮ extrapolation with small # obs. ◮ interacations of m j Model slide 3 of 15
Random Partition s = ( s 1 , . . . , s n ) = cluster membership indicators s i ∈ { 1 , . . . , J } . Let y ⋆ j and x ⋆ j variables by cluster and S j = { i : s i = j } . Model slide 4 of 15
Random Partition s = ( s 1 , . . . , s n ) = cluster membership indicators s i ∈ { 1 , . . . , J } . Let y ⋆ j and x ⋆ j variables by cluster and S j = { i : s i = j } . Random partition: p ( s | x ) , favor clusters homogeneous in x i . Model slide 4 of 15
Random Partition s = ( s 1 , . . . , s n ) = cluster membership indicators s i ∈ { 1 , . . . , J } . Let y ⋆ j and x ⋆ j variables by cluster and S j = { i : s i = j } . Random partition: p ( s | x ) , favor clusters homogeneous in x i . Sampling model: exchangeable within clusters J � � p ( y | s , x , ξ ) = p ( y i | ξ j ) j =1 i ∈ S j Model slide 4 of 15
Random Partition s = ( s 1 , . . . , s n ) = cluster membership indicators s i ∈ { 1 , . . . , J } . Let y ⋆ j and x ⋆ j variables by cluster and S j = { i : s i = j } . Random partition: p ( s | x ) , favor clusters homogeneous in x i . Sampling model: exchangeable within clusters J � � p ( y | s , x , ξ ) = p ( y i | ξ j ) j =1 i ∈ S j Prediction: future patient i = n + 1 is ◮ matched with one of the earlier clusters, on the basis of similar covariates x i = ( c i , m i , b i ). ◮ predict similar PFS. That’s all! Model slide 4 of 15
Covariate dependent partition Random partition: J � c ( S j ) g ( x ⋆ p ( s | x ) ∝ j ) j =1 favor clusters homogeneous in x i ; Model slide 5 of 15
Covariate dependent partition Random partition: J � c ( S j ) g ( x ⋆ p ( s | x ) ∝ j ) j =1 favor clusters homogeneous in x i ; with g ( x ⋆ j ) scoring “similarity” of x ⋆ j = ( x i ; i ∈ S j ); special case of PPM (Hartigan, 1990; Barry & Hartigan 1993) Model slide 5 of 15
Covariate dependent partition Random partition: J � c ( S j ) g ( x ⋆ p ( s | x ) ∝ j ) j =1 favor clusters homogeneous in x i ; with g ( x ⋆ j ) scoring “similarity” of x ⋆ j = ( x i ; i ∈ S j ); special case of PPM (Hartigan, 1990; Barry & Hartigan 1993) Similarity function: over observed covariates only. Assume only 1 covariate: g ( x ⋆ j ) = g ( { x i , i ∈ S j Model slide 5 of 15
Covariate dependent partition Random partition: J � c ( S j ) g ( x ⋆ p ( s | x ) ∝ j ) j =1 favor clusters homogeneous in x i ; with g ( x ⋆ j ) scoring “similarity” of x ⋆ j = ( x i ; i ∈ S j ); special case of PPM (Hartigan, 1990; Barry & Hartigan 1993) Similarity function: over observed covariates only. Assume only 1 covariate: g ( x ⋆ j ) = g ( { x i , i ∈ S j and x i observed } ) S ⋆ j = S j ∩ { i : x i observed } Model slide 5 of 15
Default construction – single covariate x i ℓ : with auxiliary model � j q ( x i | ξ j ) and aux prior q ( ξ j ) ⇒ i ∈ S ⋆ � � g ( x ⋆ j ) = q ( x i | ξ j ) q ( ξ j ) d ξ j i ∈ S ⋆ j analytical evaluation with conjugate pairs q ( x | ξ ) , q ( ξ ) for continuous, binary, count etc. Easy extension to mv continous vector etc. Model slide 6 of 15
Default construction – single covariate x i ℓ : with auxiliary model � j q ( x i | ξ j ) and aux prior q ( ξ j ) ⇒ i ∈ S ⋆ � � g ( x ⋆ j ) = q ( x i | ξ j ) q ( ξ j ) d ξ j i ∈ S ⋆ j analytical evaluation with conjugate pairs q ( x | ξ ) , q ( ξ ) for continuous, binary, count etc. Easy extension to mv continous vector etc. Multiple covariates: for mix of multiple data types L � g ( x ⋆ j ) = g ℓ ( x ⋆ j ℓ ) ℓ =1 with product over covariates (covariate subvectors) Model slide 6 of 15
Computation j ): scale with q ( x i ℓ | ¯ ξ ℓ ) for any choice of ¯ Scaled g ( x ⋆ ξ g ℓ ( x ∗ j ℓ ) g ℓ ( x ∗ ˜ j ℓ ) = ξ ℓ ) , i ∈ S j q ( x i ℓ | ¯ � Model slide 7 of 15
Recommend
More recommend