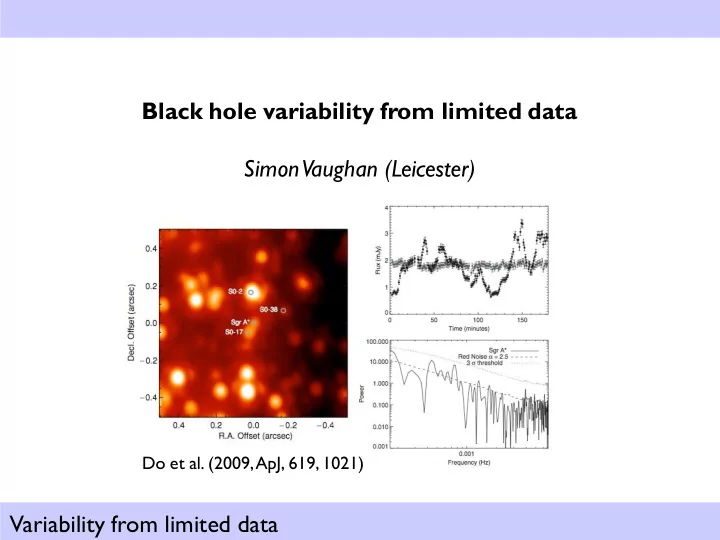
Black hole variability from limited data Simon Vaughan (Leicester) - PowerPoint PPT Presentation

Black hole variability from limited data Simon Vaughan (Leicester) Do et al. (2009, ApJ, 619, 1021) Variability from limited data

Outline 1. The periodogram (as a spectral estimator) 2. Problems with interpretation 3. In reverse: simulation from the periodogram 4. Few-cycle periods 5. Spectral analysis with short time series a. Maximum likelihood fitting b. Model checking of noise spectra c. Testing for periods 6. Things to watch out for 7. List of books, references for further reading Variability from limited data

Spectral analysis? Y ou‟ve been doing it for years! Variability from limited data

The periodogram: from the DFT... N 1 N 1 X ( f ) x exp( 2 if t ) x exp( 2 ijk / N ) j k j k k k 0 k 0 f j / N t ( j 0 , 1 , ..., N / 2 ) j t k t ( k 0 , 1 , ..., N 1 ) k 2 t 2 P ( f ) A | X ( f ) | e.g. A j j 2 N x N 1 X ( f ) x cos( 2 jk / N ) ix sin( 2 jk / N ) j k k k 0 N 1 N 1 x cos( 2 jk / N ) i x sin( 2 jk / N ) k k k 0 k 0 N 1 R x cos( 2 jk / N ) k R iI k 0 j j N 1 2 2 2 1 I x sin( 2 jk / N ) P ( f ) | X ( f ) | R I tan I / R k j j j j j k 0 Variability from limited data

The periodogram: from the DFT... N 1 R x cos( 2 jk / N ) k k 0 N 1 I x sin( 2 jk / N ) k k 0 If x k are independent and identically (iid) distributed random variables (with a Normal distribution) – i.e. “white noise” – then R j and I j are also Normally distributed. And independent at all j (in the asymptotic limit N ). This follows from the Central Limit Theorem : the sum (or mean) of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately Normally distributed Let‟s consider a very simple case with t = 1 Expected value (mean of x ) = 0 N / 2 N / 2 N / 2 1 1 N / 2 2 2 2 var P f P 2 2 Variance (of x ) 2 = j j N N N j 0 j 0 j 0 Spectrum 2 = 2 Variability from limited data

The periodogram: distribution of ordinates 2 2 1 R 1 I R ~ exp I ~ exp 2 2 2 2 2 2 prob ( P ) dp prob ( R ) prob ( I ) dRdI Multiplication rule prob ( R ) prob ( I ) 2 rdr 2 2 2 ( R I ) 2 2 2 exp rdr P r R I rdr dP / 2 2 2 2 2 1 P 2 exp dP M 2 2 2 2 2 imag 1 r= P exp( P / M ) M I dr real R Exponential distribution of periodogram ordinates Note : does not depend on N . Variability from limited data

The periodogram: exponential distribution (a.k.a. chi square, 2 df) Expected value (mean ) = M 1 p ( P ) exp( P / M ) Variance ( 2 ) = M 2 M Std dev./mean ( / ) =100% This distribution holds even when M j is a function of j (i.e. not white) 1 exp( 1 ) 0 . 632 exp( 1 ) 0 . 368 Variability from limited data

The periodogram: exponential distribution (a.k.a. chi square, 2 df) Expected value (mean ) = 2 1 p ( X ) exp( X / 2 ) Variance ( 2 ) = 2 2 = 4 2 Std dev./mean ( / ) = 100% Chi-square distribution , with 2 degrees of freedom: 2 X ~ 2 Since R and I are independently and identically (iid) Normally 2 P ~ M / 2 distributed, the sum of squares j j 2 2 2 P R I j j j is chi-square distributed with 2 df. Gamma( /2, 2) Chi-square( ) Exponential Variability from limited data

The periodogram (as a spectral estimator) The periodogram is badly behaved (100% std. dev.) regardless of the amount of data. We say it is an inconsistent estimator of the (true) spectrum. The most popular spectral estimate (in astronomy, at least) is the averaged periodogram, where periodograms from each of M non-overlapping intervals are averaged. This is known as „Barlett‟s method‟ after M. S. Bartlett (1948, Nature, 161, 686-687) Variability from limited data

The periodogram : Bartlett‟s method L 1 ( l ) Q P j j L l 1 L L L 1 1 1 ( l ) ( l ) E [ Q ] E P E P M M j j j j j L L L l 1 l 1 l 1 2 M L L L 1 1 1 j ( l ) ( l ) 2 V [ Q ] V P V P M j j j j 2 2 L L L L l 1 l 1 l 1 The Bartlett averaged periodogram is a consistent spectral estimator, because the variance decreases with more data (larger L ). Ideally we use independent realisations of our process, x ( t ) , but in practice we use non- overlapping time segments and hope this will do (assumed ergodic ). But we are therefore limited to N /2 L frequencies, with resolution L / N . We gain in variance reduction (of our estimator) but lose in frequency resolution. Variability from limited data

Examples of natural spectra Rat Electroencephalogram during Slow Wave Sleep Ambient noise spectrum from a depth of 8,413 m in the Mariana Trench. A black hole Variability from limited data

Interpreting periodograms • Usually better to use log-log plots: • log(y): more symmetric distribution of ordinates • log(y): a natural choice for exponential distribution • log-log: power law spectrum becomes linear • But remember mean(log[x]) ≠ log(mean[x]) • Watch out for biases ( leakage and/or aliasing ) A message from Captain Data : “ More lives have been lost looking at the raw periodogram than by any other action involving time series !” (J. Tukey 1980; quoted by D. Brillinger, 2002) Variability from limited data

Interpreting periodograms: aliasing Aliasing „folds‟ power from frequencies above the Nyquist sampling frequency 1 f f 2 t onto frequencies below the Nyquist frequency 1 f f 2 t This tends to flatten spectra at high frequencies. Greatly reduced by binning continuous data. Variability from limited data

Interpreting periodograms: leakage Finite duration of time series (discontinuity at ends) causes broadening or smearing of the power density. When the intrinsic spectrum is steep (e.g. ~1/ f 2 ) this leads to a fraction of the (large) power at low frequencies leaking to higher frequencies (which have much lower intrinsic power). Hardly matters for spectra flatter than ~1/ f . Can be reduced by taking longer observations (!) or tapering (yuk!) Variability from limited data

Leakage & aliasing in sparse & finite data Variability from limited data

In reverse: simulating noise from spectra Variability from limited data

In reverse: simulating noise from spectra Now we know how the periodogram of a noise process relates to its spectrum, we can run the argument backwards, to generate a realisation of a noise process from a spectrum. 1. compute spectrum P ( f ) at j 1 , 2 , ..., N / 2 j 2. generate two sets of N / 2 random numbers X and Y from the standard Normal distributi on j j 3. Make a complex ve ctor C P / 2 X iY j j j j (set Y 0 at Nyquist frequency) * 4. Mirror in negative frequencie s C C j j 5. Inverse Fourier tr ansform x(t) FT{C} • Davies & Harte (1987, Biometrica , 74, 95) • Timmer & Konig (1995, A&A , 300, 707) Variability from limited data

In reverse: simulating noise from spectra Now we know how the periodogram of a noise process relates to its spectrum, we can run the argument backwards, to generate a realisation of a noise process from a spectrum. 1. compute spectrum P ( f ) at j 1 , 2 , ..., N / 2 j 2 2. generate N/ 2 random numbers X from the distributi on j 2 3. multiply t hese together to get a fake periodogra m S P X j j j 4. generate N/ 2 random phases over [ , ) j (set 0 at Nyquist frequency) 5. Make a complex ve ctor C S / 2 exp( i ) j j j * 6. Mirror in negative frequencie s C C j j 7. Inverse Fourier tr ansform x(t) FT{C} • Davies & Harte (1987, Biometrica , 74, 95) • Timmer & Konig (1995, A&A , 300, 707) Variability from limited data

Simulation in pictures: model power spectrum Variability from limited data

Simulation in pictures: fake periodogram (randomised power spectrum) Variability from limited data

Simulation in pictures: random phases Variability from limited data

Simulation in pictures: the faked complex DFT Negative frequencies (packaged here) Real bit Imaginary bit Variability from limited data

Simulation in pictures: inverse the DFT to get a time series Variability from limited data

Noise simulation examples Variability from limited data

Noise simulation examples Variability from limited data

Noise simulation To make realistic time series (i.e. that include aliasing and/or leakage) generate data series that are much longer than N t and/or sampled much faster than t . This is easily done in the Davies-Harte method: extrapolate power spectral model to lower/higher frequencies f j j / VN t j 1 , 2 , ..., J J VWN / 2 Where V > 1 is „oversampling‟ factor for lowest frequency, and W > 1 is „oversampling‟ factor for highest frequency. (FFTs are fast, so don‟t worry about it!) You can add other effects (e.g. realistic Poisson noise) afterwards. My advice : the best way to get a feel for how sampling affects power spectrum estimation is to simulate lots of data, with lots of different spectral shapes, and different sampling, and see how your spectrum estimates looks. Variability from limited data