Big-O-ology Problem You can only run a few test cases. There will be - PowerPoint PPT Presentation

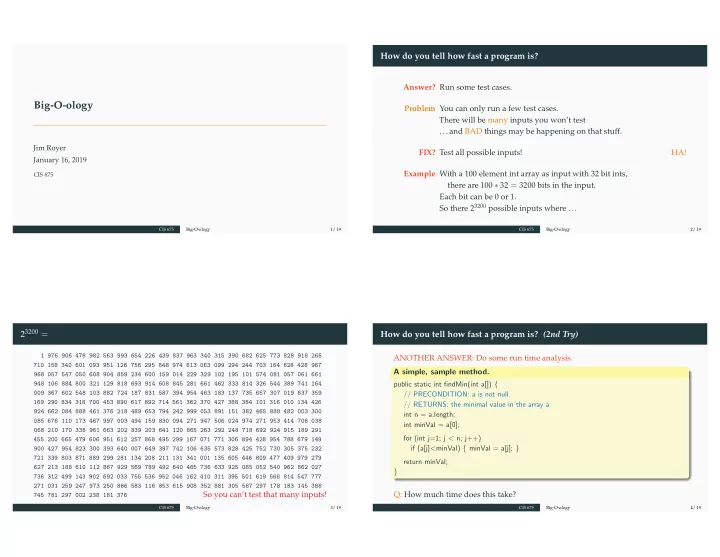
How do you tell how fast a program is? Answer? Run some test cases. Big-O-ology Problem You can only run a few test cases. There will be many inputs you won’t test ...and BAD things may be happening on that stuff. Jim Royer FIX? Test all possible inputs! HA! January 16, 2019 Example With a 100 element int array as input with 32 bit ints, CIS 675 there are 100 ∗ 32 = 3200 bits in the input. Each bit can be 0 or 1. So there 2 3200 possible inputs where ... CIS 675 Big-O-ology 1/ 19 CIS 675 Big-O-ology 2/ 19 2 3200 = How do you tell how fast a program is? (2nd Try) 1 976 906 478 982 563 993 654 226 439 837 963 340 315 390 682 625 773 828 918 265 ANOTHER ANSWER: Do some run time analysis. 710 158 340 601 093 951 126 756 295 848 974 613 063 099 294 244 703 164 628 428 967 A simple, sample method. 968 057 547 050 608 904 859 234 600 159 014 229 329 102 195 101 574 081 057 061 661 948 106 884 800 321 129 818 693 914 608 845 281 661 462 333 814 326 544 389 741 164 public static int findMin(int a[]) { 009 367 602 548 103 882 724 187 831 587 394 954 463 183 137 735 657 307 019 637 359 // PRECONDITION: a is not null. 169 290 834 318 700 453 890 617 892 714 561 362 370 427 388 384 101 316 010 134 426 // RETURNS: the minimal value in the array a 924 662 084 888 461 376 218 489 653 794 242 999 053 891 151 382 465 888 482 003 300 int n = a.length; 085 676 110 173 467 997 003 494 159 830 094 271 947 506 024 974 271 953 414 706 038 int minVal = a[0]; 068 210 170 338 961 663 202 839 203 641 120 865 263 292 248 718 692 924 915 189 291 for (int j=1; j < n; j++) 455 200 665 479 606 951 612 257 868 495 299 167 071 771 306 894 428 954 788 679 149 if (a[j] < minVal) { minVal = a[j]; } 900 427 954 823 300 393 640 007 649 397 742 106 635 573 828 425 752 730 305 375 232 721 339 803 871 889 299 281 134 208 211 131 341 001 135 605 446 809 477 409 979 279 return minVal; 627 213 188 610 112 867 929 569 789 492 640 465 736 633 925 065 052 540 962 862 027 } 736 312 499 143 902 692 033 755 536 952 046 162 410 311 395 501 619 568 814 547 777 271 031 259 247 973 250 866 583 116 853 615 908 352 881 305 587 297 178 183 145 388 So you can’t test that many inputs! Q: How much time does this take? 745 781 297 002 238 181 376 CIS 675 Big-O-ology 3/ 19 CIS 675 Big-O-ology 4/ 19

How much time does findMin take? Dealing with Problem 1: Different size arrays produce different run times Obvious fix: Problems with the question: • Make the answer depend on the length of the array: 1. Different size arrays will produce different run times. T ( n ) = the run time for a length n array Example You would expect findMin to take longer on a length • Finding T ( n ) exactly is usually hard . 100000 array than on a length 3 array. 2. On a particular input, you will see different run times under: • But an estimate is almost always good enough. • different machines • different Java compilers • different Java run-time systems WARNING: Oversimplified. CIS 675 Big-O-ology 5/ 19 CIS 675 Big-O-ology 6/ 19 Dealing with Problem 2: Different setups produce different run times Dealing with Problem 2: Different setups produce different run times Assumption 1: Proportionality Given two setups, there are constants c low and c high such that Assumption 2: Straight-line code takes constant time the run-time for setup 1 on a size n input • Straight-line code = code with no loops or recursions. c low ≤ the run-time for setup 2 on a size n input ≤ c high . • The constant depends on the setup (of machine, compiler, ...). Example Example (Code: straight-line and otherwise) • Suppose we have two computers, an old W ONDERBOX 4 and a new ✓ if (a[j] < minVal) { minVal = a[j]; } W ONDERBOX C LOUD 9. ✓ n = a.length; minVal = a[0]; • We expect programs on the newer machine to be between 2.5 and 3.8 times ✖ for (j=1; j < n; j++) faster than the old one. if (a[j] < minVal) { minVal = a[j]; } WARNING: Also oversimplified. CIS 675 Big-O-ology 7/ 19 CIS 675 Big-O-ology 8/ 19

Back to: How much time does findMin take? A Second Example public static void selectionSort(int a[]) { public static int findMin(int a[]) { // PRECONDITION: a is not null. int n = a.length, minVal = a[0]; // POSTCONDITION: a is sorted in increasing order for (int j=1; j < n; j++) int i, j, minj, minVal, n = a.length; if (a[j] < minVal) { minVal = a[j]; } ( ⋆ ) return minVal; for (i=0; i < n-1; i++) { } // find minj ∈ { i, . . . ,n-1 } ∋ a[minj] = min { a[j] : i ≤ j ≤ n-1 } Analysis minj = i; minVal = a[i]; • ( ⋆ ) is the straight line code that is buried deepest in for-loops. for (j=i+1; j < n; j++) on • For a given value of n , ( ⋆ ) is executed n − 1 times. if (a[j] < minVal) { minj = j; minVal = a[j]; } ( ∗ ) board • So, for a given setup, there are constants c low and c high ∋ // Swap the values of a[i] and a[minj] a[minj] = a[i]; a[i] = minVal; c low · ( n − 1 ) ≤ ≤ c high · ( n − 1 ) . the run time of findMin // Now: a[0] ≤ a[1] ≤ · · · ≤ a[i] ≤ min { a[j] : i < j ≤ n-1 } } // end of for-loop • Use testing to get estimates for c low and c high . } // end of selectionSort CIS 675 Big-O-ology 9/ 19 CIS 675 Big-O-ology 10/ 19 A Second Example A Second Example Big-O-ology Big-O-ology public static void selectionSort(int a[]) { public static void selectionSort(int a[]) { // PRECONDITION: a is not null. // PRECONDITION: a is not null. 2019-01-16 2019-01-16 // POSTCONDITION: a is sorted in increasing order // POSTCONDITION: a is sorted in increasing order int i, j, minj, minVal, n = a.length; int i, j, minj, minVal, n = a.length; for (i=0; i < n-1; i++) { for (i=0; i < n-1; i++) { // find minj ∈ { i, . . . ,n-1 } ∋ a[minj] = min { a[j] : i ≤ j ≤ n-1 } // find minj ∈ { i, . . . ,n-1 } ∋ a[minj] = min { a[j] : i ≤ j ≤ n-1 } minj = i; minVal = a[i]; Analysis minj = i; minVal = a[i]; Analysis for (j=i+1; j < n; j++) on for (j=i+1; j < n; j++) on if (a[j] < minVal) { minj = j; minVal = a[j]; } ( ∗ ) if (a[j] < minVal) { minj = j; minVal = a[j]; } ( ∗ ) board board // Swap the values of a[i] and a[minj] // Swap the values of a[i] and a[minj] A Second Example a[minj] = a[i]; a[i] = minVal; A Second Example a[minj] = a[i]; a[i] = minVal; // Now: a[0] ≤ a[1] ≤ · · · ≤ a[i] ≤ min { a[j] : i < j ≤ n-1 } // Now: a[0] ≤ a[1] ≤ · · · ≤ a[i] ≤ min { a[j] : i < j ≤ n-1 } } // end of for-loop } // end of for-loop } // end of selectionSort } // end of selectionSort Step 1: Identify the pieces of straightline code that are buried deepest. Step 2: Count how many times these innermost pieces of the program are executed for a given value of n . if (a[j]<minVal) { minJ = j; minVal = a[j]; } In selectionSort this is: We handle the two loops in selectionSort one at a time, starting with the innermost. since it occurs within both loops. Whereas both for (j=i+1; j<n; j++) T HE INNERMOST LOOP : This is • minJ = i; minVal = a[i]; if (a[j]<minVal) { minJ = j; minVal = a[j]; } • a[minJ] = a[i]; a[i] = minVal; So: • the first iteration has j==i+1 , the last iteration has j==n-1 , and j increases by 1 with occur within only the outermost loop. each iteration. • there are (n-1) - (i+1) +1 == n-i-1 many iterations. • for particular values of i and n the innermost code is executed n-i-1 times every time the innermost for loop is executed.