FU B ERLIN 2006 PN & Systems Biology P ATHWAY A NALYSIS OF B IOCHEMICAL N ETWORKS WITH P ETRI N ETS Monika Heiner Brandenburg University of Technology Cottbus Dep. of CS monika.heiner@informatik.tu-cottbus.de May 2006 C ONTENTS PN & Systems Biology BASIC NOTIONS proper T-invariants -> Pascoletti 1986 ❑ minimal T-invariants -> Lautenbach 1973 ❑ elementary modes -> Schuster 1991 ❑ extreme pathways -> Schilling, Schuster, Palson 1999 ❑ generic pathways -> Bockmayr 2005 ❑ MODULAR COMPUTATION approach -> Zaitsev 2005 ❑ (preliminary) results -> Lehrack 2006 (to appear) ❑ monika.heiner@informatik.tu-cottbus.de May 2006
PN & Systems Biology P ETRI N ETS - B ASICS monika.heiner@informatik.tu-cottbus.de May 2006 P ETRI N ETS , B ASICS - THE S TRUCTURE PN & Systems Biology atomic actions -> Petri net transitions -> chemical reactions ❑ 2 NAD + + 2 H 2 O -> 2 NADH + 2 H + + O 2 NADH NAD + 2 2 input output 2 H + r1 compounds compounds 2 H 2 O O 2 hyperarc 2 NAD + 2 NADH 2 H + 2 H 2 O O 2 monika.heiner@informatik.tu-cottbus.de May 2006
P ETRI N ETS , B ASICS - THE S TRUCTURE PN & Systems Biology atomic actions -> Petri net transitions -> chemical reactions ❑ 2 NAD + + 2 H 2 O -> 2 NADH + 2 H + + O 2 NADH NAD + 2 2 input output 2 H + r1 compounds compounds 2 H 2 O O 2 local conditions -> Petri net places -> chemical compounds ❑ multiplicities -> Petri net arc weights -> stoichiometric relations ❑ condition’s state -> token(s) in its place -> available amount (e.g. mol) ❑ system state -> marking -> compounds distribution ❑ PN = (P, T, F, m 0 ), F: (P x T) U (T x P) -> N 0 , m 0 : P -> N 0 ❑ monika.heiner@informatik.tu-cottbus.de May 2006 P ETRI N ETS , B ASICS - THE B EHAVIOUR PN & Systems Biology atomic actions -> Petri net transitions -> chemical reactions ❑ 2 NAD + + 2 H 2 O -> 2 NADH + 2 H + + O 2 NADH NAD + 2 2 input output 2 H + r1 compounds compounds 2 H 2 O O 2 TOKEN GAME FIRING NADH NAD + 2 2 DYNAMIC BEHAVIOUR 2 H + r1 (substance/signal flow) 2 H 2 O O 2 monika.heiner@informatik.tu-cottbus.de May 2006
B IOCHEMICAL P ETRI NETS , S UMMARY PN & Systems Biology biochemical networks ❑ -> networks of (abstract) chemical reactions biochemically interpreted Petri net ❑ -> partial order sequences of chemical reactions (= elementary actions) transforming input into output compounds / signals [ respecting the given stoichiometric relations, if any ] -> set of all pathways from the input to the output compounds / signals [ respecting the stoichiometric relations, if any ] pathway ❑ -> self-contained partial order sequence of elementary (re-) actions monika.heiner@informatik.tu-cottbus.de May 2006 PN & Systems Biology I NVARIANT A NALYSES monika.heiner@informatik.tu-cottbus.de May 2006
I NCIDENCE M ATRIX C PN & Systems Biology a representation of the net structure => stoichiometric matrix ❑ P T t1 . . . . . . tj tm p1 C = cij = (pi, tj) = F(tj,pi) - F(pi, tj) = ∆ tj(pi) pi cij ∆ tj ∆ tj = ∆ tj(*) . . . pn matrix entry cij : ❑ token change in place pi by firing of transition tj matrix column ∆ tj : ❑ vector describing the change of the whole marking by firing of tj side-conditions are neglected ❑ cij = 0 i enzyme x x j a enzyme-catalysed b reaction monika.heiner@informatik.tu-cottbus.de May 2006 T- INVARIANTS , B ASICS I PN & Systems Biology Lautenbach, 1973 ❑ T-invariants ❑ -> multisets of transitions , ≠ , ≥ -> integer solutions x of -> Parikh vector Cx = 0 x 0 x 0 minimal T-invariants ❑ -> there is no T-invariant with a smaller support -> sets of transitions -> gcD of all entries is 1 any T-invariant is a non-negative linear combination of minimal ones ❑ -> multiplication with a positive integer ∑ kx = aixi -> addition i -> Division by gcD Covered by T-Invariants (CTI) ❑ -> each transition belongs to a T-invariant monika.heiner@informatik.tu-cottbus.de May 2006
T- INVARIANTS , B ASICS II PN & Systems Biology a T-invariant defines a subnet -> partial order structure ❑ -> the T-invariant’s transitions (the support), + all their pre- and post-places + the arcs in between -> pre-sets of supports = post-sets of supports -> ANALOGUE DEFINITIONS FOR P - INVARIANTS , ≠ , ≥ yC = 0 y 0 y 0 monika.heiner@informatik.tu-cottbus.de May 2006 T- INVARIANTS , T WO I NTERPRETATIONS IN B IO N ET - PN & Systems Biology WORKS T-invariants = (multi-) sets of transitions = Parikh vector ❑ -> zero effect on marking -> reproducing a marking / system state partially ordered transition sequence -> behaviour understanding ❑ of transitions occuring one after the other -> substance / signal flow -> signal transduction networks, gene regulatory networks relative transition firing rates ❑ of transitions occuring permanently & concurrently -> steady state behaviour -> metabolic networks monika.heiner@informatik.tu-cottbus.de May 2006
T- INVARIANTS , B ASIC T YPES IN B IO N ETWORKS PN & Systems Biology trivial minimal T-invariants ❑ -> reversible reactions -> boundary transitions of ab A B auxiliary compounds ba non-trivial minimal T-invariants ❑ -> i/o-T-invariants gB covering boundary transitions of rB input / output compounds B -> inner cycles monika.heiner@informatik.tu-cottbus.de May 2006 E XAMPLE , T- INVARIANTS PN & Systems Biology ❑ substances involved -> input substance A gA -> output substance C gA gA -> auxiliary substance B A A A ab inv5 ab inv4 ac inv1 gA ab rb B rB B C C rC A B C inv2 ab ac gB bc rC gB gB rC B rB B C bc inv3 rB papin2003.spped monika.heiner@informatik.tu-cottbus.de May 2006
E XAMPLE , E LEMENTARY M ODES PN & Systems Biology ❑ substances involved -> input substance A gA gA -> output substance C gA -> auxiliary substance B A A A ab ab inv5 inv4 ac inv1 gA ab rb B B C rB C rC A B C inv2 gB bc rC ab ac gB gB rC B rB B C bc no elementary mode inv3 rB papin2003.spped monika.heiner@informatik.tu-cottbus.de May 2006 E XAMPLE , E XTREME P ATHWAYS PN & Systems Biology ❑ substances involved no extreme pathway -> input substance A gA -> output substance C gA gA -> auxiliary substance B A A A ab inv5 ab inv4 ac inv1 gA ab rb B rB B C C rC A B C inv2 ab ac gB bc rC gB gB rC B rB B C bc no elementary mode inv3 rB papin2003.spped monika.heiner@informatik.tu-cottbus.de May 2006
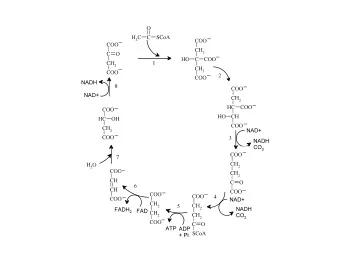
E XAMPLE , E XTREME P ATHWAYS PN & Systems Biology ❑ substances involved no extreme pathway -> input substance A gA gA -> output substance C gA -> auxiliary substance B A A A ab ab inv5 inv4 ac inv1 gA ab rb B B C rB C rC + A B C inv2 gB bc rC ab ac - gB gB rC B rB B C bc inv4 = inv5 + inv2 - inv3 inv3 rB papin2003.spped monika.heiner@informatik.tu-cottbus.de May 2006 E LEMENTARY T- INVARIANTS / H ILBERT BASIS PN & Systems Biology g_Gluc five additional T-invariants four minimal T-invariants Gluc r1_5 inv5 = (inv1 + inv3) / 2 1. Gluc -> r7 -> 2 Pyr GAP inv6 = (inv2 + inv4) / 2 2. Gluc -> r7 -> 2 Lac 2 3. Gluc -> r7a, r7b -> 2 Pry r6 inv7 = (inv1 + inv2) / 2 4. Gluc -> r7a, r7b -> 2 Lac inv8 = (inv3 + inv4) / 2 BPS r7a r7 inv9 = (inv1 + inv2 + inv3 + inv4) / 4 DPG r7b 1 Lac r7 2 Lac r7 -> Gluc -> -> Gluc -> 3PG 1 Pyr 2 Pyr r7a, r7b r7a, r7b r8_10 Pyr ∑ ∑ kx = aixi x = aixi r_Pyr r11 i i Lac r_Lac monika.heiner@informatik.tu-cottbus.de May 2006
PN & Systems Biology MODULAR COMPUTATION monika.heiner@informatik.tu-cottbus.de May 2006 B ASIC I DEA PN & Systems Biology decomposition ❑ p1 into subnets t6 t4 for each subnet: t1 ❑ 6 2 computation of 3 t5 (local) invariants p2 p3 p5 p4 3 computation of ❑ 6 interface invariants t3 t2 calculation of ❑ system invariants subnet - transition-bordered conflict cluster C, -> by composition of defined by its places subnet invariants all postplaces of input transitions belong to C -> guided by all preplaces of output transitions belong to C interface invariants each interface transition has at most - one input subnet - one output subnet monika.heiner@informatik.tu-cottbus.de May 2006
Recommend
More recommend
