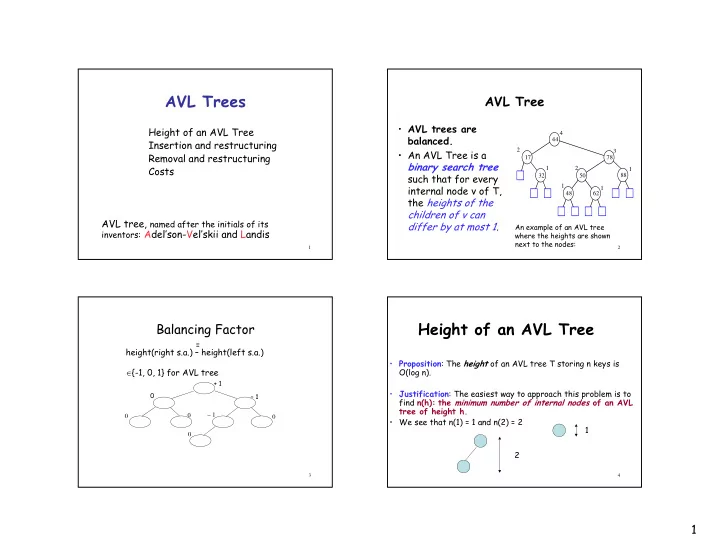
AVL Trees AVL Tree AVL trees are Height of an AVL Tree 4 - PowerPoint PPT Presentation

AVL Trees AVL Tree • AVL trees are Height of an AVL Tree 4 balanced. 44 Insertion and restructuring • An AVL Tree is a 2 3 Removal and restructuring 17 78 binary search tree Costs 1 2 1 such that for every 32 50 88 internal node v of T, 1 1 48 62 the heights of the children of v can AVL tree, named after the initials of its differ by at most 1. An example of an AVL tree inventors: Adel’son-Vel’skii and Landis where the heights are shown next to the nodes: 1 2 Height of an AVL Tree Balancing Factor = height(right s.a.) – height(left s.a.) • Proposition : The height of an AVL tree T storing n keys is ∈ {-1, 0, 1} for AVL tree O(log n). + 1 • Justification : The easiest way to approach this problem is to 0 – 1 find n(h): the minimum number of internal nodes of an AVL tree of height h. – 1 0 0 0 • We see that n(1) = 1 and n(2) = 2 1 0 2 3 4 1

n(h): the minimum number of internal nodes of Height of an AVL Tree an AVL tree of height h. For n ≥ 3, an AVL tree of height n(h) = 1 + n(h-1) + n(h-2) h contains the root node, one AVL subtree of height h-1 and the other AVL subtree of h-2 height h-2. h h-1 h-2 h-1 But: n(h-1) > n(h-2), that is: n(h) > 1+ n(h-2) +n(h-2) which is > 2n(h-2) i.e. n(h) = 1 + n(h-1) + n(h-2) so n(h) > 2n(h-2) 5 6 Height of an AVL Tree n(h) > 2 i n(h-2i) with n(1) = 1 So, now we know: n(h) > 2n(h-2) n(2) = 2 n(h) > 2n(h-4)= 2 2n(h-4) but then also: n(h-2) > 2n(h-4) h-2i = 1 n(h) > 4n(h-4) for i = h/2 - 1 n(h) > 2 h/2 - 1 n(1) but then also: n(h-4) > 2n(h-6) n(h) > 8n(h-4) n(h) > 2 h/2 - 1 We can continue: log n(h) > log 2 h/2 - 1 n(h) > 2n(h-2) log n(h) > h/2 - 1 n(h) > 4n(h-4) … h < 2 log n(h) + 2 n(h) > 2 i n(h-2i) which means that h is O(log n) 7 8 2

Insertion Insertion Before After left After right insertion insertion • A binary search tree T is called balanced if for every A 0 A – 1 A + 1 node v, the height of v’s children differ by at most one. • Inserting a node into an AVL tree involves performing an expandExternal(w) on T, which changes the heights A + 1 + 2 A 0 of some of the nodes in T. A • If an insertion causes T to become unbalanced re-balancing we have to rebalance... A – 1 – 2 A 0 A 9 10 re-balancing Rebalancing Rebalancing after insertion Step 1: Trace the path back from the point of insertion to the first node whose grandparent is unbalanced. Label this node x, its parent y, and grandparent z. We are going to identify 3 nodes which form a Examples ….. grandparent, parent, child triplet and the 4 subtrees attached to them. We will rearrange z z these elements to create a new balanced tree. y y x x 11 12 3

Rebalancing Rebalancing Step 3: Rename x, y, z to a, b, c according to their Step 2: These nodes will have 4 subtrees connected inorder traversal i.e. if y< x < z then label y ‘a’, x to them. Label them T 1 , T 2 , T 3 , T 4 from left to right. ‘b’ and z ‘c’. Examples ….. Example z z c = z y y a =y x T 4 x T 4 T 1 b = x T 3 T 1 T 2 T 3 T 2 13 14 Rebalancing Example c Step 4: Replace the tree rooted at z with the 44 z 6 following tree: a 17 78 7 2 y 32 50 b 88 1 4 x b 3 48 62 5 T 3 54 a c T 2 T 0 T 1 b 44 4 x 17 62 6 a 2 z y c T 1 T 2 T 3 T 4 32 1 50 3 78 7 5 48 54 88 Rebalance done! T 2 T 0 T 1 T 3 15 16 4

Example 1 Does this really work? a We need to see that the new tree is : z y b y a) A Binary search tree - the inorder traversal z x of our new tree should be the same as that of h the old tree c x T 1 h+2 h h h h-1 h b) Balanced: have we fixed the problem? T 2 h-1 T 1 T 2 T 3 T 4 h T 3 T 4 We consider 2 types of examples Inorder: T1 z T2 y T3 x T4 17 18 Example 2 An Observation… x c z Notice that in both cases, the new tree rooted at y z b has the same height as the old tree rooted at z a y had before insertion. b h x h h-1 h h So.. once we have done one rebalancing act, we are h+2 T 4 h done. T 1 T 2 T 3 T 4 h-1 h T 1 T 2 T 3 Inorder: T1 y T2 x T3 z T4 19 20 5

rebalance (v) T1 <- a.left; T4 <- c.right x <- v; Y <- x.parent; z <- y.parent b.left <- a; b.right <- c Removal while (z.isBalanced and not(z.isRoot) ) a.left <- T1; a.right <- T2 x <- y; y <- z; z <- z.parent c.left <- T3; c.right <- T4 if ( not z.isBalanced) T1.parent <- a; T2.parent <-a • We can easily see that performing a if ( x = y.left) { x<=y} T3.parent <- b; T3.parent <- c removeAboveExternal(w) can cause T to become if (y = z.left) {x<=y<=z} a <- x; b <- y; c<- z; unbalanced. if (z.isRoot) then T2 <- x.right; T3 <- y.right; root <- b • Let z be the first unbalanced node encountered while else { z<=x<=y} b.parent <- NULL a <- z; b <- x; c <- y; travelling up the tree from w. Also, let y be the child of else if (z.isLeftChild) T2 <- x.left; T3 <- x.right; z.parent.left<-b z with the larger height, and let x be the child of y else {y<=x} else z.parent.right <- b with the larger height. if (y = z.left) {y<=x<=z} b.parent <- z.parent a <- y; b <- x; c <- z; a.parent <- b; c.parent <- b • We can perform operation restructure(x) to restore T2 <- x.left; T3 <- x.right balance at the subtree rooted at z. else { z<=y<=x} • As this restructuring may upset the balance of another a <- z; b <- y; c <- x; T2 <- y.left; T3 <- x.left node higher in the tree, we must continue checking for balance until the root of T is reached 21 22 Removal (contd.) Removal (contd.) • we could choose a different x: the choice of x is not unique !!! a z z 4 a Oh no, unbalanced! 44 4 y c 1 44 b 3 y 17 62 Oh no, 1 x 3 b c 2 17 62 2 x 50 78 unbalanced! 1 0 2 1 2 1 T 0 50 78 48 54 88 1 0 1 1 T 0 48 54 88 32 T 2 T 1 T 3 T 2 32 T 3 T 1 b y 4 x 4 62 z x 50 3 a c Whew, 2 z y 44 78 2 Whew, 3 2 44 balanced! 62 1 0 1 1 1 1 17 50 balanced! 2 88 17 48 54 78 1 1 0 1 48 54 T 2 88 23 24 T 0 T 0 T 3 T 1 T 2 6

COMPLEXITY Searching: findElement(k): Inserting: insertItem(k, o): Removing: removeElement(k): O(log n) 25 7