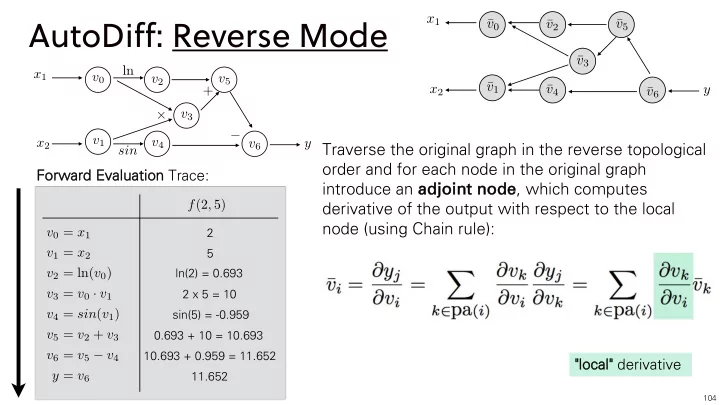
autodiff reverse mode
play

AutoDiff: Reverse Mode v 0 v 5 v 2 v 3 ln x 1 v 0 v 5 v 2 v 1 - PowerPoint PPT Presentation

Mar 13, 2024 •332 likes •980 views

x 1 AutoDiff: Reverse Mode v 0 v 5 v 2 v 3 ln x 1 v 0 v 5 v 2 v 1 + x 2 v 4 y v 6 + v 3 v 1 Traverse the original graph in the reverse topological v 4 x 2 y v 6 sin order and for each node in the original

  1. x 1 ¯ ¯ ¯ AutoDiff: Reverse Mode v 0 v 5 v 2 ¯ v 3 ln x 1 v 0 v 5 v 2 ¯ v 1 ¯ + x 2 v 4 ¯ y v 6 + v 3 − v 1 Traverse the original graph in the reverse topological v 4 x 2 y v 6 sin order and for each node in the original graph Forwar ard Eval valuat ation Trace: introduce an ad adjo join int node node , which computes f (2 , 5) derivative of the output with respect to the local node (using Chain rule): 2 v 0 = x 1 v 1 = x 2 5 ln(2) = 0.693 v 2 = ln( v 0 ) 2 x 5 = 10 v 3 = v 0 · v 1 sin(5) = -0.959 v 4 = sin ( v 1 ) v 5 = v 2 + v 3 0.693 + 10 = 10.693 v 6 = v 5 − v 4 10.693 + 0.959 = 11.652 "local cal" derivative y = v 6 11.652 104

  2. AutoDiff: Reverse Mode ln x 1 v 0 v 5 v 2 + + v 3 Backwards Derivative Backw ackwar ards Derivat vative ve Trace: − v 1 v 4 x 2 y v 6 sin ∂ v 3 ∂ v 2 1 v 0 = ¯ ¯ + ¯ = ¯ v 3 v 1 + ¯ 5.5 v 3 v 2 v 2 Forwar ard Eval valuat ation Trace: ∂ v 0 ∂ v 0 v 0 ∂ v 1 ∂ v 0 ∂ v 3 ∂ v 4 f (2 , 5) = ¯ v 3 v 0 + ¯ v 4 cos ( v 1 ) 1.716 v 1 = ¯ ¯ 1 = ¯ + ¯ v 3 v 4 ∂ v 1 ∂ v 1 ∂ v 1 ∂ v 1 ∂ v ∂ v 5 2 v 0 = x 1 = ¯ v 5 · (1) 1x1 = 1 ¯ v 2 = ¯ v 5 ∂ v 2 v 1 = x 2 5 ∂ v 2 ∂ v 5 ln(2) = 0.693 v 2 = ln( v 0 ) = ¯ v 5 · (1) 1x1 = 1 v 3 = ¯ ¯ v 5 ∂ v 3 ∂ v 3 2 x 5 = 10 v 3 = v 0 · v 1 ∂ v 6 = ¯ v 6 · ( − 1) sin(5) = -0.959 v 4 = sin ( v 1 ) 1x-1 = -1 ¯ v 4 = ¯ v 6 ∂ v 4 ∂ v 4 v 5 = v 2 + v 3 0.693 + 10 = 10.693 ∂ v 6 = ¯ v 6 · 1 ¯ v 5 = ¯ 1x1 = 1 v 6 v 6 = v 5 − v 4 10.693 + 0.959 = 11.652 ∂ v 5 ∂ v 5 ∂ y v 6 = ∂ y y = v 6 11.652 1 ¯ ∂ v 6 105

  3. AutoDiff: Reverse Mode ln x 1 v 0 v 5 v 2 + + v 3 Backwards Derivative Backw ackwar ards Derivat vative ve Trace: − v 1 v 4 x 2 y v 6 sin ∂ v 3 ∂ v 2 1 v 0 = ¯ ¯ + ¯ = ¯ v 3 v 1 + ¯ 5.5 v 3 v 2 v 2 Forwar ard Eval valuat ation Trace: ∂ v 0 ∂ v 0 v 0 ∂ v 1 ∂ v 0 ∂ v 3 ∂ v 4 f (2 , 5) = ¯ v 3 v 0 + ¯ v 4 cos ( v 1 ) 1.716 v 1 = ¯ ¯ 1 = ¯ + ¯ v 3 v 4 ∂ v 1 ∂ v 1 ∂ v 1 ∂ v 1 ∂ v ∂ v 5 2 v 0 = x 1 = ¯ v 5 · (1) 1x1 = 1 ¯ v 2 = ¯ v 5 ∂ v 2 v 1 = x 2 5 ∂ v 2 ∂ v 5 ln(2) = 0.693 v 2 = ln( v 0 ) = ¯ v 5 · (1) 1x1 = 1 v 3 = ¯ ¯ v 5 ∂ v 3 ∂ v 3 2 x 5 = 10 v 3 = v 0 · v 1 ∂ v 6 = ¯ v 6 · ( − 1) sin(5) = -0.959 v 4 = sin ( v 1 ) 1x-1 = -1 ¯ v 4 = ¯ v 6 ∂ v 4 ∂ v 4 v 5 = v 2 + v 3 0.693 + 10 = 10.693 ∂ v 6 = ¯ v 6 · 1 ¯ v 5 = ¯ 1x1 = 1 v 6 v 6 = v 5 − v 4 10.693 + 0.959 = 11.652 ∂ v 5 ∂ v 5 ∂ y v 6 = ∂ y y = v 6 11.652 1 ¯ ∂ v 6 106

  4. AutoDiff: Reverse Mode ln x 1 v 0 v 5 v 2 + + v 3 Backwards Derivative Backw ackwar ards Derivat vative ve Trace: − v 1 v 4 x 2 y v 6 sin ∂ v 3 ∂ v 2 1 v 0 = ¯ ¯ + ¯ = ¯ v 3 v 1 + ¯ 5.5 v 3 v 2 v 2 Forwar ard Eval valuat ation Trace: ∂ v 0 ∂ v 0 v 0 ∂ v 1 ∂ v 0 ∂ v 3 ∂ v 4 f (2 , 5) = ¯ v 3 v 0 + ¯ v 4 cos ( v 1 ) 1.716 v 1 = ¯ ¯ 1 = ¯ + ¯ v 3 v 4 ∂ v 1 ∂ v 1 ∂ v 1 ∂ v 1 ∂ v ∂ v 5 2 v 0 = x 1 = ¯ v 5 · (1) 1x1 = 1 v 2 = ¯ ¯ v 5 ∂ v 2 v 1 = x 2 5 ∂ v 2 ∂ v 5 ln(2) = 0.693 v 2 = ln( v 0 ) = ¯ v 5 · (1) 1x1 = 1 v 3 = ¯ ¯ v 5 ∂ v 3 ∂ v 3 2 x 5 = 10 v 3 = v 0 · v 1 ∂ v 6 = ¯ v 6 · ( − 1) sin(5) = -0.959 v 4 = sin ( v 1 ) 1x-1 = -1 ¯ v 4 = ¯ v 6 ∂ v 4 ∂ v 4 v 5 = v 2 + v 3 0.693 + 10 = 10.693 ∂ v 6 = ¯ v 6 · 1 ¯ v 5 = ¯ 1x1 = 1 v 6 v 6 = v 5 − v 4 10.693 + 0.959 = 11.652 ∂ v 5 ∂ v 5 ∂ y v 6 = ∂ y y = v 6 11.652 1 1 ¯ ∂ v 6 107

  5. AutoDiff: Reverse Mode ln x 1 v 0 v 5 v 2 + + v 3 Backwards Derivative Backw ackwar ards Derivat vative ve Trace: − v 1 v 4 x 2 y v 6 sin ∂ v 3 ∂ v 2 1 v 0 = ¯ ¯ + ¯ = ¯ v 3 v 1 + ¯ 5.5 v 3 v 2 v 2 Forwar ard Eval valuat ation Trace: ∂ v 0 ∂ v 0 v 0 ∂ v 1 ∂ v 0 ∂ v 3 ∂ v 4 f (2 , 5) = ¯ v 3 v 0 + ¯ v 4 cos ( v 1 ) 1.716 v 1 = ¯ ¯ 1 = ¯ + ¯ v 3 v 4 ∂ v 1 ∂ v 1 ∂ v 1 ∂ v 1 ∂ v ∂ v 5 2 v 0 = x 1 = ¯ v 5 · (1) 1x1 = 1 v 2 = ¯ ¯ v 5 ∂ v 2 v 1 = x 2 5 ∂ v 2 ∂ v 5 ln(2) = 0.693 v 2 = ln( v 0 ) = ¯ v 5 · (1) 1x1 = 1 v 3 = ¯ ¯ v 5 ∂ v 3 ∂ v 3 2 x 5 = 10 v 3 = v 0 · v 1 ∂ v 6 = ¯ v 6 · ( − 1) sin(5) = -0.959 v 4 = sin ( v 1 ) 1x-1 = -1 ¯ v 4 = ¯ v 6 ∂ v 4 ∂ v 4 v 5 = v 2 + v 3 0.693 + 10 = 10.693 ∂ v 6 = ¯ v 6 · 1 ¯ v 5 = ¯ 1x1 = 1 v 6 v 6 = v 5 − v 4 10.693 + 0.959 = 11.652 ∂ v 5 ∂ v 5 ∂ y v 6 = ∂ y y = v 6 11.652 1 1 ¯ ∂ v 6 108

  6. AutoDiff: Reverse Mode ln x 1 v 0 v 5 v 2 + + v 3 Backwards Derivative Backw ackwar ards Derivat vative ve Trace: − v 1 v 4 x 2 y v 6 sin ∂ v 3 ∂ v 2 1 v 0 = ¯ ¯ + ¯ = ¯ v 3 v 1 + ¯ 5.5 v 3 v 2 v 2 Forwar ard Eval valuat ation Trace: ∂ v 0 ∂ v 0 v 0 ∂ v 1 ∂ v 0 ∂ v 3 ∂ v 4 f (2 , 5) = ¯ v 3 v 0 + ¯ v 4 cos ( v 1 ) 1.716 v 1 = ¯ ¯ 1 = ¯ + ¯ v 3 v 4 ∂ v 1 ∂ v 1 ∂ v 1 ∂ v 1 ∂ v ∂ v 5 2 v 0 = x 1 = ¯ v 5 · (1) 1x1 = 1 v 2 = ¯ ¯ v 5 ∂ v 2 v 1 = x 2 5 ∂ v 2 ∂ v 5 ln(2) = 0.693 v 2 = ln( v 0 ) = ¯ v 5 · (1) 1x1 = 1 v 3 = ¯ ¯ v 5 ∂ v 3 ∂ v 3 2 x 5 = 10 v 3 = v 0 · v 1 ∂ v 6 = ¯ v 6 · ( − 1) sin(5) = -0.959 v 4 = sin ( v 1 ) 1x-1 = -1 ¯ v 4 = ¯ v 6 ∂ v 4 ∂ v 4 v 5 = v 2 + v 3 0.693 + 10 = 10.693 ∂ v 6 = ¯ v 6 · 1 ¯ v 5 = ¯ 1x1 = 1 v 6 v 6 = v 5 − v 4 10.693 + 0.959 = 11.652 ∂ v 5 ∂ v 5 ∂ y v 6 = ∂ y y = v 6 11.652 1 1 ¯ ∂ v 6 109

  7. AutoDiff: Reverse Mode ln x 1 v 0 v 5 v 2 + + v 3 Backwards Derivative Backw ackwar ards Derivat vative ve Trace: − v 1 v 4 x 2 y v 6 sin ∂ v 3 ∂ v 2 1 v 0 = ¯ ¯ + ¯ = ¯ v 3 v 1 + ¯ 5.5 v 3 v 2 v 2 Forwar ard Eval valuat ation Trace: ∂ v 0 ∂ v 0 v 0 ∂ v 1 ∂ v 0 ∂ v 3 ∂ v 4 f (2 , 5) = ¯ v 3 v 0 + ¯ v 4 cos ( v 1 ) 1.716 v 1 = ¯ ¯ 1 = ¯ + ¯ v 3 v 4 ∂ v 1 ∂ v 1 ∂ v 1 ∂ v 1 ∂ v ∂ v 5 2 v 0 = x 1 = ¯ v 5 · (1) 1x1 = 1 v 2 = ¯ ¯ v 5 ∂ v 2 v 1 = x 2 5 ∂ v 2 ∂ v 5 ln(2) = 0.693 v 2 = ln( v 0 ) = ¯ v 5 · (1) 1x1 = 1 v 3 = ¯ ¯ v 5 ∂ v 3 ∂ v 3 2 x 5 = 10 v 3 = v 0 · v 1 ∂ v 6 = ¯ v 6 · ( − 1) sin(5) = -0.959 v 4 = sin ( v 1 ) 1x-1 = -1 ¯ v 4 = ¯ v 6 ∂ v 4 ∂ v 4 v 5 = v 2 + v 3 0.693 + 10 = 10.693 ∂ v 6 = ¯ v 6 · 1 ¯ v 5 = ¯ 1x1 = 1 v 6 v 6 = v 5 − v 4 10.693 + 0.959 = 11.652 ∂ v 5 ∂ v 5 ∂ y v 6 = ∂ y y = v 6 11.652 1 1 ¯ ∂ v 6 110

  8. AutoDiff: Reverse Mode ln x 1 v 0 v 5 v 2 + + v 3 Backwards Derivative Backw ackwar ards Derivat vative ve Trace: − v 1 v 4 x 2 y v 6 sin ∂ v 3 ∂ v 2 1 v 0 = ¯ ¯ + ¯ = ¯ v 3 v 1 + ¯ 5.5 v 3 v 2 v 2 Forwar ard Eval valuat ation Trace: ∂ v 0 ∂ v 0 v 0 ∂ v 1 ∂ v 0 ∂ v 3 ∂ v 4 f (2 , 5) = ¯ v 3 v 0 + ¯ v 4 cos ( v 1 ) 1.716 v 1 = ¯ ¯ 1 = ¯ + ¯ v 3 v 4 ∂ v 1 ∂ v 1 ∂ v 1 ∂ v 1 ∂ v ∂ v 5 2 v 0 = x 1 = ¯ v 5 · (1) 1x1 = 1 v 2 = ¯ ¯ v 5 ∂ v 2 v 1 = x 2 5 ∂ v 2 ∂ v 5 ln(2) = 0.693 v 2 = ln( v 0 ) = ¯ v 5 · (1) 1x1 = 1 v 3 = ¯ ¯ v 5 ∂ v 3 ∂ v 3 2 x 5 = 10 v 3 = v 0 · v 1 ∂ v 6 = ¯ v 6 · ( − 1) sin(5) = -0.959 v 4 = sin ( v 1 ) 1x-1 = -1 ¯ v 4 = ¯ v 6 ∂ v 4 ∂ v 4 v 5 = v 2 + v 3 0.693 + 10 = 10.693 ∂ v 6 = ¯ v 6 · 1 1x1 = 1 v 5 = ¯ ¯ 1x1 = 1 v 6 v 6 = v 5 − v 4 10.693 + 0.959 = 11.652 ∂ v 5 ∂ v 5 ∂ y v 6 = ∂ y y = v 6 11.652 1 1 ¯ ∂ v 6 111

  9. AutoDiff: Reverse Mode ln x 1 v 0 v 5 v 2 + + v 3 Backwards Derivative Backw ackwar ards Derivat vative ve Trace: − v 1 v 4 x 2 y v 6 sin ∂ v 3 ∂ v 2 1 v 0 = ¯ ¯ + ¯ = ¯ v 3 v 1 + ¯ 5.5 v 3 v 2 v 2 Forwar ard Eval valuat ation Trace: ∂ v 0 ∂ v 0 v 0 ∂ v 1 ∂ v 0 ∂ v 3 ∂ v 4 f (2 , 5) = ¯ v 3 v 0 + ¯ v 4 cos ( v 1 ) 1.716 v 1 = ¯ ¯ 1 = ¯ + ¯ v 3 v 4 ∂ v 1 ∂ v 1 ∂ v 1 ∂ v 1 ∂ v ∂ v 5 2 v 0 = x 1 = ¯ v 5 · (1) 1x1 = 1 v 2 = ¯ ¯ v 5 ∂ v 2 v 1 = x 2 5 ∂ v 2 ∂ v 5 ln(2) = 0.693 v 2 = ln( v 0 ) = ¯ v 5 · (1) 1x1 = 1 v 3 = ¯ ¯ v 5 ∂ v 3 ∂ v 3 2 x 5 = 10 v 3 = v 0 · v 1 ∂ v 6 = ¯ v 6 · ( − 1) sin(5) = -0.959 v 4 = sin ( v 1 ) 1x-1 = -1 ¯ v 4 = ¯ v 6 ∂ v 4 ∂ v 4 v 5 = v 2 + v 3 0.693 + 10 = 10.693 ∂ v 6 = ¯ v 6 · 1 1x1 = 1 v 5 = ¯ ¯ 1x1 = 1 v 6 v 6 = v 5 − v 4 10.693 + 0.959 = 11.652 ∂ v 5 ∂ v 5 ∂ y v 6 = ∂ y y = v 6 11.652 1 1 ¯ ∂ v 6 112

  10. AutoDiff: Reverse Mode ln x 1 v 0 v 5 v 2 + + v 3 Backwards Derivative Backw ackwar ards Derivat vative ve Trace: − v 1 v 4 x 2 y v 6 sin ∂ v 3 ∂ v 2 1 v 0 = ¯ ¯ + ¯ = ¯ v 3 v 1 + ¯ 5.5 v 3 v 2 v 2 Forwar ard Eval valuat ation Trace: ∂ v 0 ∂ v 0 v 0 ∂ v 1 ∂ v 0 ∂ v 3 ∂ v 4 f (2 , 5) = ¯ v 3 v 0 + ¯ v 4 cos ( v 1 ) 1.716 v 1 = ¯ ¯ 1 = ¯ + ¯ v 3 v 4 ∂ v 1 ∂ v 1 ∂ v 1 ∂ v 1 ∂ v ∂ v 5 2 v 0 = x 1 = ¯ v 5 · (1) 1x1 = 1 v 2 = ¯ ¯ v 5 ∂ v 2 v 1 = x 2 5 ∂ v 2 ∂ v 5 ln(2) = 0.693 v 2 = ln( v 0 ) = ¯ v 5 · (1) 1x1 = 1 v 3 = ¯ ¯ v 5 ∂ v 3 ∂ v 3 2 x 5 = 10 v 3 = v 0 · v 1 ∂ v 6 = ¯ v 6 · ( − 1) sin(5) = -0.959 v 4 = sin ( v 1 ) 1x-1 = -1 ¯ v 4 = ¯ v 6 ∂ v 4 ∂ v 4 v 5 = v 2 + v 3 0.693 + 10 = 10.693 ∂ v 6 = ¯ v 6 · 1 1x1 = 1 v 5 = ¯ ¯ 1x1 = 1 v 6 v 6 = v 5 − v 4 10.693 + 0.959 = 11.652 ∂ v 5 ∂ v 5 ∂ y v 6 = ∂ y y = v 6 11.652 1 1 ¯ ∂ v 6 113

Download Presentation
Download Policy: The content available on the website is offered to you 'AS IS' for your personal information and use only. It cannot be commercialized, licensed, or distributed on other websites without prior consent from the author. To download a presentation, simply click this link. If you encounter any difficulties during the download process, it's possible that the publisher has removed the file from their server.

Recommend

No more mini-languages: Autodiff in full-featured Python David Duvenaud, Dougal Maclaurin,

No more mini-languages: Autodiff in full-featured Python David Duvenaud, Dougal Maclaurin,

No more mini-languages: Autodiff in full-featured Python David Duvenaud, Dougal Maclaurin, Matthew Johnson Our awesome new world TensorFlow, Stan, Theano, Edward Only need to specify forward model Autodiff + inference / optimization

397 views • 27 slides
Lazy-Mode RF OSINT and Reverse Engineering Marc Newlin | @marcnewlin | TROOPERS18 $(whoami)

Lazy-Mode RF OSINT and Reverse Engineering Marc Newlin | @marcnewlin | TROOPERS18 $(whoami)

Lazy-Mode RF OSINT and Reverse Engineering Marc Newlin | @marcnewlin | TROOPERS18 $(whoami) Red Team @ Snap Former Wireless Security Researcher @ Bastille Networks Wireless CVEs in products from 21 vendors Radios

755 views • 64 slides
Second Order Reverse Mode of AD : A Vertex Elimination Perspective Mu Wang, Alex Pothen and Paul

Second Order Reverse Mode of AD : A Vertex Elimination Perspective Mu Wang, Alex Pothen and Paul

Second Order Reverse Mode of AD : A Vertex Elimination Perspective Mu Wang, Alex Pothen and Paul Hovland Computer Science, Purdue University MCS Division, Argonne National Lab Thanks : NSF, DOE, Intel October 10, 2016 Wang et.al (Purdue

1.07k views • 68 slides
SiPMs for solar neutrino detector? J. Kaspar, 6/10/14 1 SiPM is Geiger photodiode APD Mode

SiPMs for solar neutrino detector? J. Kaspar, 6/10/14 1 SiPM is Geiger photodiode APD Mode

SiPMs for solar neutrino detector? J. Kaspar, 6/10/14 1 SiPM is Geiger photodiode APD Mode APD full depletion V APD take a photo-diode reverse-bias it above breakdown voltage (Geiger mode avalanche photo diode) add

590 views • 23 slides
Automatic Differentiation for Computational Engineering Kailai Xu and Eric Darve CME 216 AD 1

Automatic Differentiation for Computational Engineering Kailai Xu and Eric Darve CME 216 AD 1

Automatic Differentiation for Computational Engineering Kailai Xu and Eric Darve CME 216 AD 1 / 47 Outline Overview 1 Computational Graph 2 Forward Mode 3 Reverse Mode 4 AD for Physical Simulation 5 AD Through Implicit Operators 6

809 views • 51 slides
Remanufacturing of Products Remanufacturing of Products and Reverse Logistics and Reverse

Remanufacturing of Products Remanufacturing of Products and Reverse Logistics and Reverse

Remanufacturing of Products Remanufacturing of Products and Reverse Logistics and Reverse Logistics Xochitl Aquiahuatl March 2007 Outline Outline Closed-loop Supply Chain Reverse Logistics Recovery Options Product

388 views • 22 slides
CS 7643: Deep Learning Topics: Computational Graphs Notation + example Computing

CS 7643: Deep Learning Topics: Computational Graphs Notation + example Computing

CS 7643: Deep Learning Topics: Computational Graphs Notation + example Computing Gradients Forward mode vs Reverse mode AD Dhruv Batra Georgia Tech Administrativia HW1 Released Due: 09/22 PS1 Solutions

1.13k views • 91 slides
Attacking the Windows Kernel Below The Root Jonathan Lindsay, Reverse Engineer in extremis

Attacking the Windows Kernel Below The Root Jonathan Lindsay, Reverse Engineer in extremis

Attacking the Windows Kernel Below The Root Jonathan Lindsay, Reverse Engineer in extremis Introduction Limited to Windows, and aimed at IA32: Outline of protected mode and the kernel Attack vectors Useful tools Examples

672 views • 36 slides
Reverse Engineering CS 166 Armen Boursalian 30 Apr 2018 Reverse Engineering Take a

Reverse Engineering CS 166 Armen Boursalian 30 Apr 2018 Reverse Engineering Take a

Reverse Engineering CS 166 Armen Boursalian 30 Apr 2018 Reverse Engineering Take a product, understand how it works Usually limited to certain aspects, not full systems Need to know a little bit about a lot of topics to gain

636 views • 11 slides
CS 4803 / 7643: Deep Learning Topics: (Finish) Computing Gradients Backprop in Conv

CS 4803 / 7643: Deep Learning Topics: (Finish) Computing Gradients Backprop in Conv

CS 4803 / 7643: Deep Learning Topics: (Finish) Computing Gradients Backprop in Conv Layers Forward mode vs Reverse mode AD Modern CNN Architectures Zsolt Kira Georgia Tech The architecture of LeNet5 Handwriting Recognition

1.16k views • 84 slides
CS 4803 / 7643: Deep Learning Topics: (Finish) Computing Gradients Backprop in Conv

CS 4803 / 7643: Deep Learning Topics: (Finish) Computing Gradients Backprop in Conv

CS 4803 / 7643: Deep Learning Topics: (Finish) Computing Gradients Backprop in Conv Layers Forward mode vs Reverse mode AD Modern CNN Architectures Zsolt Kira Georgia Tech Administrivia HW1 due date moved! Due:

1.03k views • 44 slides
Org-mode Nick Higham April 22, 2013 Nick Higham Org-mode 1 / 7 University of Manchester What

Org-mode Nick Higham April 22, 2013 Nick Higham Org-mode 1 / 7 University of Manchester What

Org-mode Nick Higham April 22, 2013 Nick Higham Org-mode 1 / 7 University of Manchester What is Org Mode? Emacs mode for note taking task management tables and spreadsheets producing L A T EX documents and web pages literate

212 views • 7 slides
Reverse Logistics Woodfield Distribution, LLC v081617 Reverse Logistics About Us Description

Reverse Logistics Woodfield Distribution, LLC v081617 Reverse Logistics About Us Description

Presentation of Capabilities Reverse Logistics Woodfield Distribution, LLC v081617 Reverse Logistics About Us Description of Services Reverse Distribution Channels DSCSA/Sustainability About Us WDSrx Woodfield Distribution, LLC Is A

454 views • 13 slides
Educational topic: FT8 digital mode What is FT8 Digital operating mode that started gaining

Educational topic: FT8 digital mode What is FT8 Digital operating mode that started gaining

Educational topic: FT8 digital mode What is FT8 Digital operating mode that started gaining momentum in 2017 Named after Its developers Steven Franke (K9AN) Joe Taylor (K1JT) Mode uses an 8-frequency shift keying format Signals occupy 50 Hz

472 views • 21 slides
1 Mor M. Peretz, Switch-Mode Power Supplies [5-4] Transistor turn off - parasitics L main

1 Mor M. Peretz, Switch-Mode Power Supplies [5-4] Transistor turn off - parasitics L main

Mor M. Peretz, Switch-Mode Power Supplies [5-1] Parasitic effects Snubbers and clamps Turn on and turn off effects Turn on - diode reverse recovery Turn off dI/dT effect on transistor Turn off diode forward recovery

256 views • 8 slides
Next-Generation Debuggers For Reverse Engineering For Reverse Engineering The ERESI team

Next-Generation Debuggers For Reverse Engineering For Reverse Engineering The ERESI team

Next-Generation Debuggers For Reverse Engineering For Reverse Engineering The ERESI team eresi@asgardlabs.org This presentation is about .. The Embedded ERESI debugger : e2dbg The Embedded ERESI tracer : etrace The ERESI reverse

849 views • 47 slides
Factor Vocab Word 2 Fraction Division Its meaning (As it is used A whole number A whole

Factor Vocab Word 2 Fraction Division Its meaning (As it is used A whole number A whole

Slide 1 / 315 Slide 2 / 315 6th Grade Fraction and Decimal Computation 2014-10-16 www.njctl.org Slide 3 / 315 Slide 4 / 315 Vocabulary words are identified with a Fraction and Decimal Computation dotted underline. Unit Topics Click on

576 views • 53 slides
Lecture 3: Word and document embeddings Plan of the lecture Part 1 : Distributional semantics

Lecture 3: Word and document embeddings Plan of the lecture Part 1 : Distributional semantics

Neural Natural Language Processing Lecture 3: Word and document embeddings Plan of the lecture Part 1 : Distributional semantics and vector spaces. Part 2 : word2vec and doc2vec models. Part 3 : Other models for word and document

1.17k views • 94 slides
Whole Numbers Jumping Jack Snap Game (numeral Cluedo Numerals! cards 0 to 20) Tell your child

Whole Numbers Jumping Jack Snap Game (numeral Cluedo Numerals! cards 0 to 20) Tell your child

1 Hougang Primary School Mathematics Workshop (P2) Make Maths Fun @ Home Whole Numbers Jumping Jack Snap Game (numeral Cluedo Numerals! cards 0 to 20) Tell your child you are thinking Draw on butcher paper numbers from one to twenty in

329 views • 4 slides
Versatility of Singular Value Decomposition (SVD) January 7, 2015 Assumption : Data = Real Data +

Versatility of Singular Value Decomposition (SVD) January 7, 2015 Assumption : Data = Real Data +

Versatility of Singular Value Decomposition (SVD) January 7, 2015 Assumption : Data = Real Data + Noise Each Data Point is a column of the n d Data Matrix A . Assumption : Data = Real Data + Noise Each Data Point is a column of the n d Data

1.04k views • 83 slides
CSE 490 Natural Language Processing Spring 2016 Introduction Yejin Choi Slides adapted

CSE 490 Natural Language Processing Spring 2016 Introduction Yejin Choi Slides adapted

CSE 490 Natural Language Processing Spring 2016 Introduction Yejin Choi Slides adapted from Dan Klein, Luke Zettlemoyer What is NLP? Fundamental goal: deep understand of broad language Not just string processing or keyword matching

579 views • 46 slides
OTHER DATA CENTER SERVICES Lecture V Ken Birman Tier two and Inner Tiers 2 If tier one

OTHER DATA CENTER SERVICES Lecture V Ken Birman Tier two and Inner Tiers 2 If tier one

CS5412 Spring 2014 (Cloud Computing: Birman) 1 CS5412: OTHER DATA CENTER SERVICES Lecture V Ken Birman Tier two and Inner Tiers 2 If tier one faces the user and constructs responses, what lives in tier two? Caching services are very

660 views • 49 slides
Creating Tutorial Materials as Lecture Supplements by Integrating Drawing Tablet and Video

Creating Tutorial Materials as Lecture Supplements by Integrating Drawing Tablet and Video

Creating Tutorial Materials as Lecture Supplements by Integrating Drawing Tablet and Video Capturing/Sharing Computer Science Education Research Conference CSERC19 / Nov 18 / Larnaca, Cyprus Chen-Wei Wang York University, Toronto, Canada

254 views • 23 slides
Bigtable: A Distributed Storage System for Structured Data Fay Chang, Jeffrey Dean, Sanjay

Bigtable: A Distributed Storage System for Structured Data Fay Chang, Jeffrey Dean, Sanjay

Bigtable: A Distributed Storage System for Structured Data Fay Chang, Jeffrey Dean, Sanjay Ghemawat, Wilson C. Hsieh, Deborah A. Wallach, Mike Burrows, Tushar Chandra, Andrew Fikes, Robert E. Gruber Google, Inc. Presented by: Robina Bhatia

499 views • 20 slides

More recommend