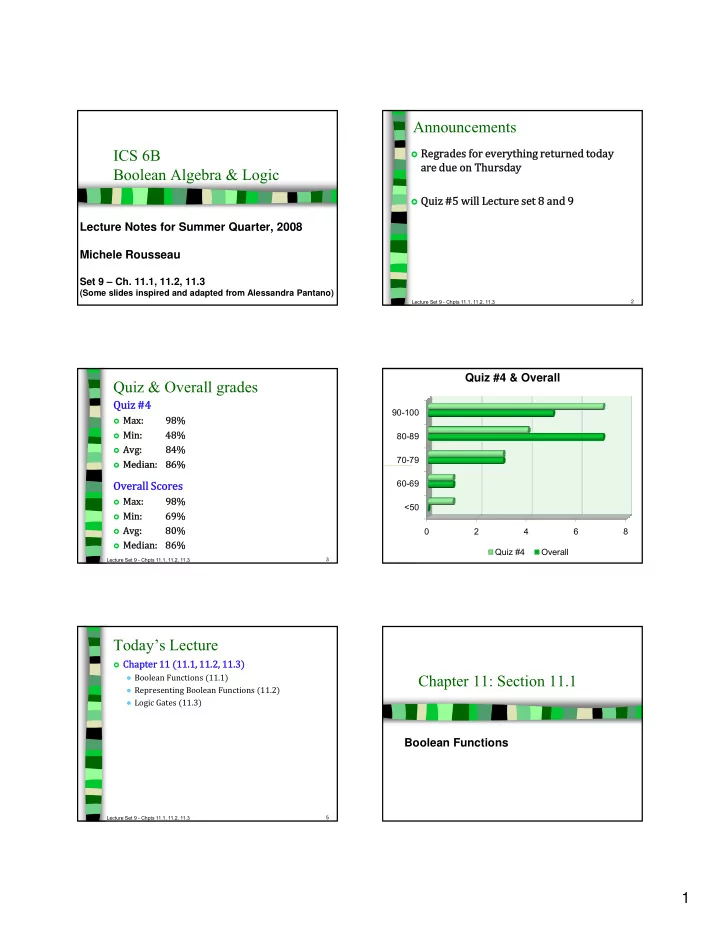
Announcements ICS 6B Regrades for everything returned today are - PDF document

Announcements ICS 6B � Regrades for everything returned today are due on Thursday Boolean Algebra & Logic � Quiz #5 will Lecture set 8 and 9 Lecture Notes for Summer Quarter, 2008 Michele Rousseau Set 9 – Ch. 11.1, 11.2, 11.3 (Some slides inspired and adapted from Alessandra Pantano) 2 Lecture Set 9 - Chpts 11.1, 11.2, 11.3 Quiz #4 & Overall Quiz & Overall grades Quiz #4 90-100 � Max: 98% � Min: 48% 80-89 � Avg: 84% 70-79 � Median: 86% � Median: 86% Overall Scores 60-69 � Max: 98% <50 � Min: 69% � Avg: 80% 0 2 4 6 8 � Median: 86% Quiz #4 Overall Lecture Set 9 - Chpts 11.1, 11.2, 11.3 3 Lecture Set 9 - Chpts 11.1, 11.2, 11.3 4 Today’s Lecture � Chapter 11 �11.1, 11.2, 11.3� ● Boolean Functions �11.1� Chapter 11: Section 11.1 ● Representing Boolean Functions �11.2� ● Logic Gates �11.3� Boolean Functions Lecture Set 9 - Chpts 11.1, 11.2, 11.3 5 1

Order of Operations Boolean Functions Examples � In order to evaluate these we need to 2‐degree Boolean functions understand the order of preference ● Things in Parenthesis come first F�x,y� � � �x�y� · �xy� � � x � � �xy� ● Then ◘ 1 – Complement l F�x,y����x�y��y�� � xy ◘ 2 – Product ◘ 3 – Sum 7 8 Lecture Set 9 - Chpts 11.1, 11.2, 11.3 Lecture Set 9 - Chpts 11.1, 11.2, 11.3 Example More Examples F�x,y�� ��x � y� � y� � � xy � Compute the values of the Boolean function Let x�0, y�1 F�x,y� � x � � y ��� 0 � 1� � 1� � � 0·1 � we use a Table with columns x, y, � y, Do the complement Do the complement x � � y � F�x, y� before the product before the sum It i It is convenient to have i t t h � ��1 � 1� � 1� � 1·1 this intermediate step x y ¬ y F(x,y)=x+¬ y � � 1 � 1 � � 1 � 1 � 1 � 1 0 0 1 1 0 1 0 0 Similarly, 1 0 1 1 1 · 0 � � �0 � 1� 1 1 0 1 � 1 · 0 � � 1 � 0 � 0 �0 Tables like this are very convenient Lecture Set 9 - Chpts 11.1, 11.2, 11.3 9 Lecture Set 9 - Chpts 11.1, 11.2, 11.3 10 More Examples Boolean Function of > 2 degrees Compute F�x,y� � x· �y � ��x � y� Boolean functions of n�3 are defined similarly. A function of degree n is a map x y �y x·�y x�y ��x�y� F�x,y��x·�y���x�y� F: �0,1� x �0,1� x … x �0,1� � �0,1� 1 0 0 1 1 0 0 n times 0 0 1 0 0 0 1 1 0 1 1 1 0 1 1 1 0 0 1 0 0 Notice that the domain of the function are bit strings + of length n: x 1 x 2 … x n, with x i �1 or 0. For each such string , F� x 1, x 2, … ,x n � can be 0 or 1 Lecture Set 1 - Admin Details. Chpts 1.1, 1.2 11 Lecture Set 9 - Chpts 11.1, 11.2, 11.3 12 2

Drawing Boolean Functions Example (of degree �3� F�x,y,z� � �x � yz is a Boolean function of degree 3 Degree 1 If F is a function of 1 Boolean variable, x y z To compute F, you need to find the �i.e. F�F�x�� 0 0 0 value of F on each of the 2 n strings then F is completely determined by F�0� and F�1�. 0 0 1 �where n degree� �where n�degree� 0 1 0 Notice that F�0� and F�1� can only be 1 or 0, so F is uniquely determined by saying whether F takes 0 1 1 in this case is n�3 so we need to find the value 1 or 0, on 1 or 0 on either of them. 1 0 0 the value of 1 0 1 2 3 � 8 strings – so the table F will Draw the length 1 strings 0 and 1 as vertices of a 1 1 0 have 8 rows segment 1 1 1 0 1 13 14 Lecture Set 9 - Chpts 11.1, 11.2, 11.3 Lecture Set 9 - Chpts 11.1, 11.2, 11.3 Boolean Functions of degree 2 Drawing Boolean Functions of degree 1 A Boolean function of degree 2 is a function of 2 Boolean Now circle the vertices on which F takes the value 1. variables x,y with values in �0,1�. We have 4 possibilities: You can think of x,y as a bit‐string of length 2. F�x� x F�x� x Both x and y can take 2 values �0 and 1�, so we have 2·2�2 2 1 1 �4 strings of length 2. 1 0 0 1 0 0 0 1 So, the total number of choices for F is 0 0 # of choices for value of F on 2 nd string. F�x� F�x� x x F�x� x 2 2·2 ·… ·2 � 2 2 � 2 4 � 16 1 1 1 0 0 1 0 1 0 1 2 2 times ‐‐ Total # of strings 0 1 We have a total of 16 possible Boolean functions. Notice that we have established a one‐to‐one correspondence 10 11 between Boolean function of degree 1 and the subsets of The 4 strings �00, 01, 10, 11� can be the set of strings of length 1. represented as the vertices of a square There are 2 strings of length 1, so there are 2 2 subsets and indeed we find 4 Boolean functions Lecture Set 9 - Chpts 11.1, 11.2, 11.3 15 00 01 16 Boolean Functions of degree 2 Drawing Boolean Functions – degree 2 We circle the vertices of which F take the value 1 10 11 10 11 10 11 10 11 It is easy to write down the corresponding function. If the vertex corresponds to a string x,y, then � 1 – if the vertex is circled 00 01 00 01 00 01 00 01 F�x,y�� 10 11 10 11 10 11 10 11 0 – if the vertex is NOT circled Example 00 01 00 01 00 01 00 01 x y F�x,y� x y F�x,y� 10 11 10 11 10 11 10 11 10 11 10 11 0 0 1 0 0 1 � � 0 1 0 0 1 1 1 0 0 1 0 1 00 01 00 01 00 01 00 01 00 01 00 01 10 11 10 11 10 11 10 11 1 1 1 1 1 0 00 01 00 01 00 01 00 01 17 Lecture Set 9 - Chpts 11.1, 11.2, 11.3 3

Drawing Boolean Functions of degree 3 Example F is defined on strings of length 3. To assign F, we decide on which strings F takes the value 1 and we circle the corresponding vertices There are 2 3 �8 such strings: x y z F�x,y,z� �000, 001, 010, 011, 100, 101, 110, 111� 1 0 0 0 0 0 0 0 0 0 1 1 W We represent the strings as vertices on a cube h i i b 101 111 101 111 1 � 0 1 0 101 111 100 110 0 100 110 0 1 1 001 011 0 1 0 0 000 010 0 1 0 1 001 011 0 1 1 0 000 010 1 1 1 1 20 Lecture Set 9 - Chpts 11.1, 11.2, 11.3 Lecture Set 9 - Chpts 11.1, 11.2, 11.3 We have one‐to‐one correspondence between Important Remark: subsets of vertices and Boolean functions. A function can be represented by many different n�3 �degree 3� expressions. � we have 2 n � 8 strings E.g. F�x��x; G�x��x�0; H�x�� � ��x� � 2 n � 8 vertices are all the same function �even if they are � 2 2 � 2 8 subsets of vertices n given by different expressions �. 2 8 B n � 2 2 � 2 2 � 2 8 Boolean functions l f ti Indeed they take the same value on every string I d d h k h l i = = General Fact: F�x��x G�x�� x+0 H�x )= ¬ (¬x) n x x x ¬x There are 2 �2 � Boolean functions of degree n. 1 1 1 0 1 1 1 �Because there are 2 n strings of length n, and you 0 0 0 1 0 0 0 can assign 2 values to each string. This gives you 2·2 ·… ·2 choices , �i.e. 2 2 Choices� n So when we say that F and G are equal, we mean that they take the same value on every string. 2 n times We do NOT require that they are defined by the same expression Lecture Set 9 - Chpts 11.1, 11.2, 11.3 21 Lecture Set 9 - Chpts 11.1, 11.2, 11.3 22 Example Boolean Identities Show that F�x� � x � x & G�x��x are the same Boolean function. We compute the tables and compare the values F�x�� x � x G�x�� x x x 1 1 1 + 1 = 1 1 0 0 0 + 0 = 0 0 = We call x+x = x a Boolean identity We also say that (x + x) and (x) are equivalent expressions. Lecture Set 9 - Chpts 11.1, 11.2, 11.3 23 Lecture Set 9 - Chpts 11.1, 11.2, 11.3 24 4