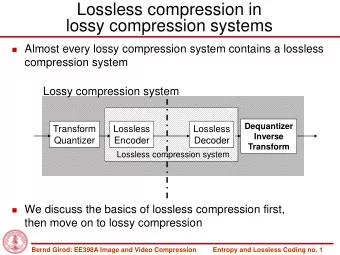
Analog-to-Digital Compression Oral PhD Exam Alon Kipnis Advisor: - PowerPoint PPT Presentation

Fundamental performance limits of Analog-to-Digital Compression Oral PhD Exam Alon Kipnis Advisor: Andrea Goldsmith 1 /32

Outline analog digital quantization 010010011001001000 sampling (lossy compression) 0100101010010001… Motivation — Factors affecting analog-to-digital conversion Main problem — Combined problem sampling and lossy compression Corollary — Optimal sampling under compression constraints Summary — Toward a unified spectral theory of analog signal processing and lossy compression 2 /32

Motivation The analog-to-digital (A/D) conversion problem: A/D conversion 010010011001 001000010000 1000100111… information loss Challenges: 1) measure 2) minimize 3 /32

Motivation: measuring information loss Minimal distortion in A/D: analog analog digital quantization 010010011001001 reconstruction sampling (lossy compression) 000010010101001 distortion A/D parameters 4 /32

Background: Lossy Compression analog quantization digital sampling analog reconstruction (lossy compression) RT bitrate: 0 . . . 00 [bits/sec] R X ( t ) 0 . . . 01 . Enc . . 0 T . . . 1 . . . 11 The Source Coding Theorem [Shannon ‘48]: Shannon’s optimization over D ( R ) distortion-rate = = probability distributions function Theoretic lower bound for distortion in A/D Ignores effect of sampling 5 /32

Background: The Sampling Theorem analog quantization digital sampling (lossy compression) f s > f Nyq , 2 f B The Sampling Theorem [Whittaker, Kotelinkov, Shannon]: X ( t ) f s ∗ t = t sinc( t ) Y [ n ] = X ( t/f s ) Ignores effect of quantization distortion f Nyq = 2 f B Shannon’s distortion-rate D ( R ) function sampling rate f s 6 /32

Combined sampling and lossy compression optimal lossy analog digital sampling compression Minimal distortion under sampling and lossy compression distortion D ( f s , R ) u n ? l = i b m i t i t r f Nyq e a Shannon’s unlimited d t e sampling rate distortion-rate D ( R ) function sampling rate f s 7 /32

Sampling under Bitrate Constraints f s > f Nyq , 2 f B The Sampling Theorem [Whittaker, Kotelinkov, Shannon] ∗ t t = X ( t ) Y [ n ] = X ( t/f s ) sinc( t ) “we are not interested in exact transmission when we have a continuous [amplitude] source, but only in transmission to within a given tolerance” [Shannon ’48] distortion D ( f s , R ) ? = f Nyq = 2 f B D ( R ) sampling rate f s Can we attain D(R) by sampling below Nyquist ? 8 /32

Motivation — Summary distortion ? D ( f s , R ) u n l i b m i t i r t ? a e = f Nyq = 2 f B t d e unlimited D ( R ) sampling rate sampling rate f s 1) What is the minimal distortion in sampling and lossy compression? 2) Can we attain D(R) by sampling below Nyquist ? 9 /32

Combined Sampling and Source Coding lossy compression reconstruction sampling f s Y [ · ] R b X ( t ) X ( t ) Dec Enc Z T ⇣ ⌘ 2 1 X ( t ) − b , D ( f s , R ) inf X ( t ) E dt T enc − dec ,T 0 Assumptions: is zero mean Gaussian stationary with PSD S X ( f ) X ( t ) S X ( f ) is unimodal S X ( f ) f Pointwise uniform sampling Y [ n ] = X ( n/f s ) 10 /32

Special case I: Gaussian Distortion Rate Function f s Y [ · ] R b X ( t ) X ( t ) Dec Enc f s > f Nyq D ( f s , R ) = D ( R ) ⇒ ( [Pinsker ’54] Z ∞ D θ ( R ) = min { S X ( f ) , θ } d f , WF ( S X ) −∞ Z ∞ R θ = 1 log + [ S X ( f ) / θ ] d (water-filling) f 2 −∞ S X ( f ) S X ( f ) θ θ D ( R ) f f R 11 /32

Special case II: MMSE in sub-Nyquist Sampling f s R Y [ · ] b X ( t ) X ( t ) Dec Enc R → ∞ D ( f s , R ) mmse ( X | Y ) mmse ( f s ) ⇒ = = MMSE in sub-Nyquist sampling [Chan & Donaldson ‘71, Matthews ’00] P S X ( f ) X S X ( f − f s k ) k S 2 X ( f − f s k ) e P S X | Y ( f ) = k ∈ Z k S X ( f − f s k ) S X ( f − f s ) S X ( f + f s ) f s f 12 /32

Combined Sampling and Source Coding f s Y [ · ] R b X ( t ) X ( t ) Dec Enc Theorem*[K., Goldsmith, Eldar, Weissman ‘13] ⇣ ⌘ e D ( f s , R ) mmse ( f s ) + WF S X | Y = e S X | Y ( f ) Distortion due to sampling θ Distortion due to bitrate constraint f s f (*) A. Kipnis, A. J. Goldsmith, T. Weissman and Y. C. Eldar, ‘Rate-distortion function of sub- Nyquist sampled Gaussian sources corrupted by noise’, Allerton 2013 13 /32

Example: Uniform PSD D ( f s , R ) vs f s ( R = 1) S X ( f ) D ( f s , R ) distortion mmse ( f s ) f f B D ( R ) f s f Nyq = 2 f B 14 /32

Achievability Scheme f s Y [ · ] R b X ( t ) X ( t ) Enc Dec e R 1 X ∆ 1 [ · ] Enc e R 2 X ∆ 2 [ · ] e Enc estimator X ( · ) orthogonalizing . * Y [ · ] transformation E [ X ( t ) | Y [ · ]] . . R k e X ∆ k [ · ] Enc X R i ≤ R i ⇣ ⌘ e D ( f s , R ) = mmse ( f s ) S X | Y WF + (*) A. Kipnis, A. J. Goldsmith and Y. C. Eldar, ‘The distortion rate function of cyclostationary Gaussian processes’, (under review) 2016 15 /32

Pre-Sampling Operation f s R b X ( t ) H ( f ) X ( t ) Dec Enc e S X | Y ( f ) e S X | Y ( f ) θ θ f s f s distortion without pre-sampling filter with pre-sampling filter H ( f ) ≡ 1 H ( f ) Linear pre-processing can reduce distortion D ( R ) f s 16 /32

Optimal pre-Sampling Filter Theorem* [K., Goldsmith, Eldar, Weissman ’14] The optimal pre-sampling filter is (i) anti-aliasing (ii) maximizes passband energy H ? ( f ) H ? ( f ) S X ( f ) no aliasing S X ( f ) θ θ f s f s | H ? | 2 S X ⇣ ⌘ D ? ( f s , R ) = mmse ? ( f s ) + WF (*) A. Kipnis, A. J. Goldsmith, Y. C. Eldar and T. Weissman, ‘Distortion-Rate function of sub-Nyquist sampled Gaussian sources’, IEEE Trans. on Information Theory, January, 2016 17 /32

Optimal pre-Sampling Filter Theorem* [K., Goldsmith, Eldar, Weissman ’14] The optimal pre-sampling filter is (i) anti-aliasing (ii) maximizes passband energy f s f s f s f s f f low-pass is optimal maximal aliasing-free set is optimal (*) A. Kipnis, A. J. Goldsmith, Y. C. Eldar and T. Weissman, ‘Distortion-Rate function of sub-Nyquist sampled Gaussian sources’, IEEE Trans. on Information Theory, January, 2016 18 /32

Why anti-aliasing is optimal ? 0 , σ 2 0 , σ 2 � � � � X 1 ∼ N X 2 ∼ N 1 2 h 1 h 2 X 1 X 2 Y + = Question: { mmse ( X 1 | Y ) + mmse ( X 2 | Y ) } argmin ? = h 1 h 2 mmse ( X i | Y ) = E ( X i − E [ X i | Y ]) 2 f s f s f s f s ∗ 1 ( σ 1 > σ 2 ) h 1 = Answer: ∗ h 2 1 ( σ 1 < σ 2 ) = f 19 /32

Critical Sub-Nyquist Sampling Rate S X ( f ) D ? ( R, f s ) vs f s (R is fixed) distortion f Nyq f R D ( R ) mmse ( f s ) f s θ θ θ f s f s f s Sub-Nyquist sampling achieves optimal distortion-rate performance f s ≥ f R D ? ( f s , R ) = D ( R ) 20 /32

Critical Sub-Nyquist Sampling Rate Theorem* [K., Goldsmith, Eldar ’15] f s ≥ f R D ? ( f s , R ) = D ( R ) Alignment of degrees of freedom Extends Kotelnikov-Whittaker-Shannon sampling theorem: Incorporates lossy compression Valid when input signal is not band limited Holds under non-uniform sampling + θ f R (*) A. Kipnis, A. J. Goldsmith and Y. C. Eldar, ‘Sub-Nyquist sampling achieves optimal rate-distortion’, Information Theory Workshop (ITW), 2015 (+) A. Kipnis, A. J. Goldsmith and Y. C. Eldar, ‘Gaussian distortion-rate function under sub- Nyquist nonuniform sampling’, Allerton 2014 21 /32

Critical Sub-Nyquist Sampling Rate critical sub-sampling ratio vs R f R f Nyq * 1 R 22 /32

Summary Transforming analog signals to bits involves sampling and lossy compression Closed-form expression for the minimal distortion as a function of the sampling rate and bitrate Parts of the signal removed due to lossy compression can be removed at the sampling stage • Sub-Nyquist sampling is optimal under bitrate constraint 23 /32

Future Work I Degrees of freedom alignment in other sampling models ? Example: compressed sensing Y ∈ R n X sampler { 0 , 1 } nR b X Dec Enc 24 /32

Noisy Input Signal quantization analog (lossy compression) digital noise sampling η ( t ) sampler f s Y [ · ] R b X ( t ) X ( t ) + Dec Enc H(f) Theorem*[K. Goldsmith, Weissman, Eldar ’13] X ( f − f s k ) | H ( f − f s k ) | 2 k S 2 P e ∗ S X | Y ( f ) = k ( S X ( f − f s k ) + S η ( f − f s k )) | H ( f − f s k ) | 2 P θ f s (*) A. Kipnis, A. J. Goldsmith, T. Weissman and Y. C. Eldar, ‘Rate-distortion function of sub- Nyquist sampled Gaussian sources corrupted by noise’, Allerton 2013 25 /32

Toward a Unified Spectral Theory of Processing Time Series Enc Dec Lossy compression e S X | Y ( f ) η ( t ) θ f s + H(f) Linear Sampling filtering Does not incorporate time-flow 26 /32

Future Work II Incorporating time-flow and lossy compression Example: minimal distortion in causal estimation under bitrate constraint X ( t ) past future t [Kolmogorov ’56]: S X ( f ) “Since a function with a bounded spectrum is always singular in the sense of my work and the θ observation of such a function is not related … to the stationary flow f of new information, then the sense of this kind of argumentation does not remain completely clear” 27 /32