CS 573: Algorithms, Fall 2013 Administrivia, Introduction CS 573: Algorithms Lecture 1 August 27, 2013 Sariel Har-Peled sariel@illinois.edu 3306 SC University of Illinois, Urbana-Champaign Fall 2013 Sariel (UIUC) CS573 1 Fall 2013 1 / 59 Sariel (UIUC) CS573 2 Fall 2013 2 / 59 The word “algorithm” comes from... Muhammad ibn Musa al-Khwarizmi 780-850 AD The word “algebra” is taken from the title of one of his books. Part I Administrivia Sariel (UIUC) CS573 3 Fall 2013 3 / 59 Sariel (UIUC) CS573 4 Fall 2013 4 / 59
Instructional Staff Online resources Instructor: Webpage: courses.engr.illinois.edu/cs573/fa2013/ 1 1 General information, homeworks, etc. ◮ Sariel Har-Peled ( sariel ) Moodle: Quizzes, solutions to homeworks. 2 Teaching Assistants: 2 Online questions/announcements: Piazza 3 Ben Raichel ( raichel2 ) 1 Online discussions, etc. David Holcomb ( dholcom2 ) 2 Office hours: See course webpage 3 Email: See course webpage 4 Sariel (UIUC) CS573 5 Fall 2013 5 / 59 Sariel (UIUC) CS573 6 Fall 2013 6 / 59 Textbooks Prerequisites 1 Asymptotic notation: O () , Ω() , o () . Prerequisites: CS 173 (discrete math), CS 225 (data structures) 1 2 Discrete Structures: sets, functions, relations, equivalence classes, partial orders, trees, graphs and CS 373 (theory of computation) 3 Logic: predicate logic, boolean algebra 4 Proofs: by induction , by contradiction Recommended books: 2 5 Basic sums and recurrences: sum of a geometric series, unrolling of recurrences, basic calculus 6 Data Structures: arrays, multi-dimensional arrays, linked lists, trees, balanced search trees, heaps Algorithms by Dasgupta, Papadimitriou & Vazirani. 1 7 Abstract Data Types: lists, stacks, queues, dictionaries, priority queues Available online for free! 8 Algorithms: sorting (merge, quick, insertion), pre/post/in order traversal of trees, depth/breadth first search of trees (maybe graphs) Algorithm Design by Kleinberg & Tardos 2 9 Basic analysis of algorithms: loops and nested loops, deriving recurrences from a recursive program Lecture notes: Available on the web-page before/during/after 3 10 Concepts from Theory of Computation: languages, automata, Turing machine, undecidability, non-determinism 11 Programming: in some general purpose language every class. 12 Elementary Discrete Probability: event, random variable, independence Additional References 13 Mathematical maturity 4 Previous class notes of Jeff Erickson, Sariel Har-Peled and the 1 instructor. Introduction to Algorithms: Cormen, Leiserson, Rivest, Stein. 2 Computers and Intractability: Garey and Johnson. 3 Sariel (UIUC) CS573 7 Fall 2013 7 / 59 Sariel (UIUC) CS573 8 Fall 2013 8 / 59
Grading Policy: Overview Homeworks Attendance/clickers: 5% One quiz every 1-2-3 weeks: Due by midnight on Sunday. 1 1 Quizzes: 5% One homework every 1-2-3 weeks. 2 2 Homeworks can be worked on in groups of up to 3 and each Homeworks: 15% 3 3 group submits one written solution (except Homework 0). Midterm: 30% 4 Short quiz-style questions to be answered individually on 1 Finals: 45% (covers the full course content) 5 Moodle . Groups can be changed a few times only. 4 Sariel (UIUC) CS573 9 Fall 2013 9 / 59 Sariel (UIUC) CS573 10 Fall 2013 10 / 59 More on Homeworks Advice No extensions or late homeworks accepted. Attend lectures, please ask plenty of questions. 1 1 To compensate, the homework with the least score will be Clickers... 2 2 dropped in calculating the homework average. Attend discussion sessions. 3 Important: Read homework faq/instructions on website. 3 Don’t skip homework and don’t copy homework solutions. 4 Study regularly and keep up with the course. 5 Ask for help promptly. Make use of office hours. 6 Sariel (UIUC) CS573 11 Fall 2013 11 / 59 Sariel (UIUC) CS573 12 Fall 2013 12 / 59
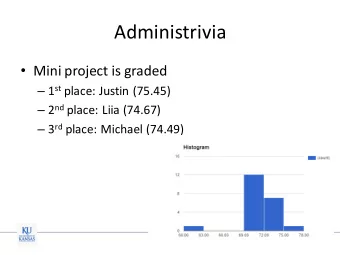
Homeworks HW 0 is posted on the class website. Quiz 0 available 1 HW 0 to be submitted in individually. 2 Part II Course Goals and Overview Sariel (UIUC) CS573 13 Fall 2013 13 / 59 Sariel (UIUC) CS573 14 Fall 2013 14 / 59 Topics Goals Some fundamental algorithms 1 1 Broadly applicable techniques in algorithm design Learn/remember some basic tricks, algorithms, problems, ideas 2 2 Understanding problem structure Understand/appreciate limits of computation (intractability) 1 3 Brute force enumeration and backtrack search 2 Appreciate the importance of algorithms in computer science 4 Reductions 3 and beyond (engineering, mathematics, natural sciences, social Recursion 4 sciences, ...) Divide and Conquer 1 Dynamic Programming Have fun!!! 2 5 Greedy methods 5 Network Flows and Linear/Integer Programming (optional) 6 Analysis techniques 3 Correctness of algorithms via induction and other methods 1 Recurrences 2 Amortization and elementary potential functions 3 Polynomial-time Reductions, NP-Completeness, Heuristics 4 Sariel (UIUC) CS573 15 Fall 2013 15 / 59 Sariel (UIUC) CS573 16 Fall 2013 16 / 59
Primality testing Problem Given an integer N > 0 , is N a prime? Part III Algorithms and efficiency SimpleAlgorithm : √ for i = 2 to ⌊ N ⌋ do if i divides N then return ‘‘COMPOSITE’’ return ‘‘PRIME’’ √ Correctness? If N is composite, at least one factor in { 2 , . . . , N } √ Running time? O ( N ) divisions? Sub-linear in input size! Wrong! Sariel (UIUC) CS573 17 Fall 2013 17 / 59 Sariel (UIUC) CS573 18 Fall 2013 18 / 59 Primality testing Efficient algorithms ...Polynomial means... in input size So, is there an efficient/good/effective algorithm for primality? How many bits to represent N in binary? ⌈ log N ⌉ bits. Question: √ N = 2 ( log N ) / 2 time. Simple Algorithm takes What does efficiency mean? Exponential in the input size n = log N . In this class efficiency is broadly equated to polynomial time . O ( n ) , O ( n log n ) , O ( n 2 ) , O ( n 3 ) , O ( n 100 ) , . . . where n is size of the input. Modern cryptography: binary numbers with 128, 256, 512 bits. 1 Simple Algorithm will take 2 64 , 2 128 , 2 256 steps! 2 Why? Is n 100 really efficient/practical? Etc. Fastest computer today about 3 petaFlops/sec: 3 × 2 50 floating 3 point ops/sec. Short answer: polynomial time is a robust, mathematically sound way to define efficiency. Has been useful for several decades. Lesson: Pay attention to representation size in analyzing efficiency of algorithms. Especially in number problems. Sariel (UIUC) CS573 19 Fall 2013 19 / 59 Sariel (UIUC) CS573 20 Fall 2013 20 / 59
TSP problem Solving TSP by a Computer Lincoln’s tour Is it hard? Circuit court - ride through 1 n = number of cities. Metamora 1 counties staying a few days in n 2 : size of input. Pekin 2 each town. Bloomington Number of possible solutions is 3 Lincoln was a lawyer traveling 2 Urbana Clinton Danville with the Eighth Judicial n ∗ ( n − 1 ) ∗ ( n − 2 ) ∗ ... ∗ 2 ∗ 1 = n ! . . t i Circuit. M k s a Springfield l u Monticello P Picture: travel during 1850. n ! grows very quickly as n grows. Decator 3 4 Sullivan Very close to optimal tour. n = 10 : n ! ≈ 3628800 1 Paris Taylorville n = 50 : n ! ≈ 3 ∗ 10 64 Might have been optimal 2 Shelbyville at the time.. n = 100 : n ! ≈ 9 ∗ 10 157 Sariel (UIUC) CS573 21 Fall 2013 21 / 59 Sariel (UIUC) CS573 22 Fall 2013 22 / 59 Solving TSP by a Computer What is a good algorithm? Fastest computer... Running time... n 2 ops n 3 ops n 4 ops Input size n ! ops 5 0 secs 0 secs 0 secs 0 secs Fastest super computer can do (roughly) 1 20 0 secs 0 secs 0 secs 16 mins 3 · 10 9 years 30 0 secs 0 secs 0 secs 2 . 5 ∗ 10 15 100 0 secs 0 secs 0 secs never 8000 0 secs 0 secs 1 secs never operations a second. 16000 0 secs 0 secs 26 secs never Assume: computer checks 2 . 5 ∗ 10 15 solutions every second, 2 32000 0 secs 0 secs 6 mins never then... 64000 0 secs 0 secs 111 mins never n = 20 = ⇒ 2 hours. 1 200,000 0 secs 3 secs 7 days never n = 25 = ⇒ 200 years. 2 2,000,000 0 secs 53 mins 202.943 years never ⇒ 2 ∗ 10 20 years!!! n = 37 = 3 10 9 years 10 8 4 secs 12.6839 years never 10 13 years 10 9 6 mins 12683.9 years never Sariel (UIUC) CS573 23 Fall 2013 23 / 59 Sariel (UIUC) CS573 24 Fall 2013 24 / 59
Recommend
More recommend
