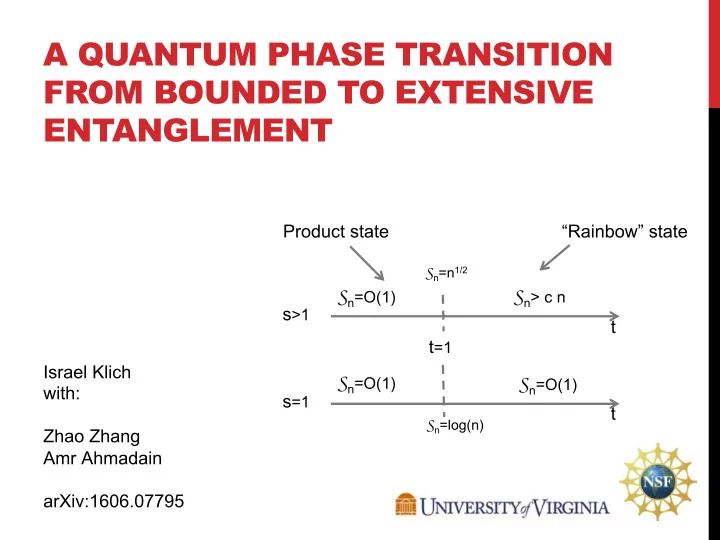

A QUANTUM PHASE TRANSITION FROM BOUNDED TO EXTENSIVE ENTANGLEMENT Product state “Rainbow” state S n =n 1/2 S n =O(1) S n > c n s >1 t t =1 Israel Klich S n =O(1) S n =O(1) with: s =1 t S n =log(n) Zhao Zhang Amr Ahmadain arXiv:1606.07795
HIGHLY ENTANGLED STATES Entanglement entropy: S A = − Tr ρ A log ρ A where ρ A = Tr B ρ Generic states in Hilbert space have extensive entanglement (page prl 93,foong prl 94,sen prl 96) ⎧ L d generic state (Page prl 93) ⎪ ⎪ L d − 1 (Hastings 07,1d) gapped , " area law " ⎪ L d − 1 log L S A ≈ ⎨ free fermions (Gioev IK 06,M Wolf 06) ⎪ c ⎪ (Holzhey Larsen Wilczek 96, 3 log L conformal Calabrese Cardy … ) ⎪ ⎩
EXTENSIVELY ENTANGLED STATES First local Hamiltonian with volume scaling: Irani 2010. local Hilbert space dimension is 21 Simpler models but without translational invariance, and with exponentially varying couplings: Gottesman Hastings 2010 Rainbow ground states:Vitagliano Riera Latorre 2010, Ramirez Rodriguez-Laguna Sierra 2014 Translationally invariant but with a square root scaling: Movassagh Shor (2014), Salberger Korepin (2016)
Here: a simple spin chain with remarkable phase transition: 1 2 n n+1 n+2 2n S n =n 1/2 S n =O(1) S n > c n s >1 t t =1 S n =O(1) S n =O(1) s =1 t S n =log(n)
Basic intuition: How to create a highly entangled state? EPR: electron-positron pair generation in an electric field as a source of entanglement “Rainbow” state
ANOTHER TYPE OF RAINBOW STATE IN THE LAB! Optical Pfister et al, 2004 frequency Chen Meniccuci Pfister PRL2014, 60 mode cluster state comb Cavity eigenmodes -n -(n-1) -1 1 n Nonlinear cavity ω in → ω n + ω − n = ω in Incoming laser
MOTZKIN WALK HAMILTONIANS Bravyi et al. 2012 “Criticality without frustration” ∑ Ψ = S n ∝ 1 2 log( n ) Motzkin paths Movassagh Shor 2014 “Power law violation of the area law in quantum spin chains” ∑ Ψ = S n ∝ n colored Motzkin paths
REPRESENTING SPIN STATES AS MOTZKIN WALKS |1 , 0 , -1 , 1 , 1 , -1 , 1 , 0 , 1 , -1 , -1 , 0 , 0 , -1 > Motzkin paths: ( - ) ( ( ) ( - ( ) ) - - ) m 1 2n n n-1 Colored Motzkin paths: |1 , 0, -1 , 2 , 1 ,-1 , 1 , 0, 2 , -2, -1 , 0, 0, -1> ( - ) [ ( ) ( - [ ] ) - - ] m 1 2n n n-1
MOTZKIN HAMILTONIANS Enforce a g.s. superposition made of Motzkin paths by using projectors like: Φ = Ψ = Θ = H = ∑ Θ Θ + Ψ Ψ + Φ Φ + h 1 + h 2 n + ( penalty unmatched colors )
HOW COLOR ENHANCES ENTROPY H eight after n steps = # of unmatched up steps For n >> 1, typical Motzkin walk is like a Brownian walk . ⇒ Typical height after n steps ∝ n ⇒ # of colorings of unmatched up steps ∝ s n all coloringschemes of unmatched equally likely ⇒ S n ∝ n
CAN WE SKEW THE MODEL TO PREFER HIGHER MOTZKIN PATHS? Main idea – up moves are like electrons and down moves are like positrons. They should go in different directions! Can try: Φ = cos ϕ i − sin ϕ i Ψ = cos ψ i − sin ψ i Θ = cos θ i − sin θ i
Choice of angles must satisfy a consistency condition: i + 1 i 1 L i +1 R i i i + 1 i i + 1 cot ψ i +1 tan φ i F i F i +1 i i + 1 cot ψ i +1 tan θ i ≡ tan φ i tan θ i +1
Local consistency condition is enough h 0 = h + 2 h h + 1 (a) h 0 = h + 2 h h + 1 (b) � 1 � 2 � 3 � 4
THE UNIFORM MODEL Φ = − t Ψ = − t Θ = − t ∑ Area t Ψ = colored Motzkin paths
ENTANGLEMENT ENTROPY Schmidt decomposition ∑ t Area Ψ = colored Motzkin paths ⎛ ⎞ ⎛ ⎞ n ⎜ ⎟ ⎜ ⎟ ∑ ∑ ∑ t Area ∑ t Area p n , m Ψ = ⊗ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ m = 0 coloring paths from 0 paths from ⎝ ⎠ ⎝ ⎠ scheme to height m height m to 0 2 ( n − m )/2 p n , m = M n , m ∑ s i ∑ t Areaunder path M n , m = N n i = 0 path from 0 to height mwith iunpaired colors n ∑ s m 2 N n = M n , m m = 0
SCALING OF ENTROPY . We need the asymptotics of M n,m ( n − m )/2 ∑ s i ∑ t Areaunder path M n , m = i = 0 path from 0 to height mwith iunpaired colors n ∫ ( dX ds ) 2 − log( t ) X ( s ) ds X ( n ) = m − ∑ t Areaunder path ∫ ≈ dX [ τ ] e 0 path from 0 to X (0) = 0 height mwith Charged particle in a field, Brownian particle with a drift
For precise estimates use recursion relations: M k + 1, k + 1 =t k + 1/2 M k , k M k + 1, k =t k M k , k + t k − 1/2 M k , k − 1 M k + 1, m =st m + 1/2 M k , m + 1 + t m M k , m + t m − 1/2 M k , m − 1 , 0 < m < k M k + 1,0 =st 1/2 M k ,1 + M k ,0 ( k, m + 1) ( k, m ) ( k + 1 , m ) ( k, m − 1) (0 , 0) ( k, 0) ( k + 1 , 0)
PROOF IDEA Define ∞ ˆ ∑ M n , m m ; Shift : M n = S m = m − 1 m = 0 Then : ! n st − ( k − 1/2) ˆ S + 1 + t ( k − 1/2) ˆ ( ) ∏ S + M n = K 0 k = 1 For large n, ! k 0 − 1 n st − ( k − 1/2) ˆ S + 1 + t ( k − 1/2) ˆ t ( k − 1/2) ˆ ( ) ( ) ∏ S + ∏ S + M n ~ K 0 + corrections k = 1 k = k 0 Transient ∝ n − k 0 Ballistic propagation of distribution
Here: a simple spin chain with remarkable phase transition: 1 2 n n+1 n+2 2n S n =n 1/2 S n =O(1) S n > c n s >1 t t =1 S n =O(1) S n =O(1) s =1 t S n =log(n)
DEFORMED FREDKIN MODEL Fredkin model Salberger/Korepin 2016 has as ground state superposition of Dyck paths: ∑ Ψ = colored Dyck paths We can deform it into: ∑ q Area under Ψ = colored Dyck paths Entropy scales linearly with n log(s)! Same phase diagram. Need 3 neighbor interactions. To appear shortly! IK with Z Zhang, O Salberger, T Udagawa, H Katsura, V Korepin
ODDS AND ENDS 1. Gap decays exponentially for t>1. Gapped for t<1? 2. Thermodynamics is unknown (Shape of transition region?) 3. Stability? 4. Periodic boundary conditions? 5. Can build a tensor network. 6. Holography: Can get linear entanglement scaling by choosing a metric that would give entanglement using Ryu Takayangi formula. Relation to hyperscaling violations (Huijse, Sachdev and Swingle 2012) ?
Recommend
More recommend