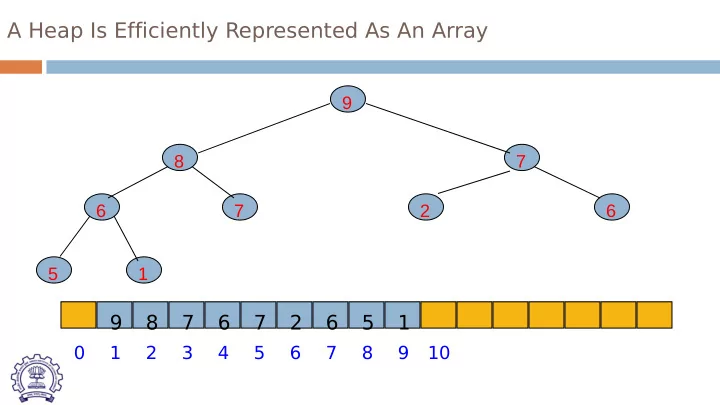
A Heap Is Efficiently Represented As An Array 9 8 7 6 7 2 6 5 - PowerPoint PPT Presentation

A Heap Is Efficiently Represented As An Array 9 8 7 6 7 2 6 5 1 9 8 7 6 7 2 6 5 1 0 1 2 3 4 5 6 7 8 9 10

Moving Up And Down A Heap 1 9 2 3 8 7 4 7 5 6 6 7 2 6 5 1 8 9

Putting An Element Into A Max Heap  Complete binary tree with 10 nodes. 9 8 7 6 7 2 6 5 1 7

Putting An Element Into A Max Heap  New element is 5. 9 8 7 6 7 2 6 5 1 7 5

Putting An Element Into A Max Heap  New element is 20. 9 8 7 6 2 6 7 5 1 7 7

Putting An Element Into A Max Heap  New element is 20. 9 8 7 6 2 6 5 1 7 7 7

Putting An Element Into A Max Heap  New element is 20. 9 7 6 8 2 6 5 1 7 7 7

Putting An Element Into A Max Heap  New element is 20. 20 9 7 6 8 2 6 5 1 7 7 7

Putting An Element Into A Max Heap  Complete binary tree with 11 nodes. 20 9 7 6 8 2 6 5 1 7 7 7

Putting An Element Into A Max Heap  New element is 15. 20 9 7 6 8 2 6 5 1 7 7 7

Putting An Element Into A Max Heap  New element is 15. 20 9 7 6 2 6 8 5 1 7 7 8 7

Putting An Element Into A Max Heap  New element is 15. 20 7 15 6 9 2 6 8 5 1 7 7 8 7

Complexity Of Put  Complexity is O(log n), where n is heap size. 20 7 15 6 9 2 6 8 5 1 7 7 8 7

Removing The Max Element  Max element is in the root. 20 7 15 6 9 2 6 8 5 1 7 7 8 7

Removing The Max Element  After max element is removed. 7 15 6 9 2 6 8 5 1 7 7 8 7

Removing The Max Element  Heap with 10 nodes. 7 15 6 9 2 6 8 5 1 7 7 8 7 Reinsert 8 into the heap.

Removing The Max Element  Reinsert 8 into the heap. 7 15 6 9 2 6 5 1 7 7 7

Removing The Max Element  Reinsert 8 into the heap. 15 7 6 9 2 6 5 1 7 7 7

Removing The Max Element  Reinsert 8 into the heap. 15 9 7 6 2 6 8 5 1 7 7 7

Removing The Max Element  Max element is 15. 15 9 7 6 2 6 8 5 1 7 7 7

Removing The Max Element  After max element is removed. 9 7 6 2 6 8 5 1 7 7 7

Removing The Max Element  Heap with 9 nodes. 9 7 6 2 6 8 5 1 7 7 7

Removing The Max Element  Reinsert 7. 9 7 6 2 6 8 5 1

Removing The Max Element  Reinsert 7. 9 7 6 2 6 8 5 1

Removing The Max Element  Reinsert 7. 9 8 7 6 7 2 6 5 1

Complexity Of Remove Max Element  Complexity is O(log n). 9 8 7 6 7 2 6 5 1

Note  Heap is not a search data-structure  You are interested in minimum or maximum depending on the heap  There are efficient ways to convert an array into a heap.  Requires O(n) time to convert an array into a heap instead of O(n log n) as suggested by n insertions.

Administrivia  TA Office Hours  Wednesdays 3 to 5 pm in the PC lab  Homework 2  Updated the PDF document  Made a few things clear; Corrected a few things  Updated the .zip file  Makefiles in both directories  Changes to hashT emplate.c file

Thank You

EE717: Advanced Computing foR ELECTRICAL Engineers Lecture 8 Graphs 24 Aug 2014 Shankar Balachandran, IIT Bombay (shankarb@ee.iitb.ac.in)

Graphs  G = (V,E)  V is the vertex set.  Vertices are also called nodes and points.  E is the edge set.  Each edge connects two different vertices.  Captures relationships between vertices  Directed edge has an orientation (u,v). u v

Graph Representation  Adjacency Matrix  Adjacency Lists  Linked Adjacency Lists  Array Adjacency Lists

Adjacency Matrix  0/1 n x n matrix, where n = # of vertices  A(i,j) = 1 iff (i,j) is an edge 1 2 3 4 5 2 0 1 0 1 0 1 3 1 0 0 0 1 2 1 0 0 0 0 1 3 4 1 0 0 0 1 4 5 0 1 1 1 0 5

Adjacency Matrix Properties 1 2 3 4 5 2 1 0 1 0 1 0 3 2 1 0 0 0 1 1 3 0 0 0 0 1 4 4 1 0 0 0 1 5 5 0 1 1 1 0 • Diagonal entries are zero. • Adjacency matrix of an undirected graph is symmetric.  A(i,j) = A(j,i) for all i and j.

Adjacency Matrix (Digraph) 1 2 3 4 5 2 1 0 0 0 1 0 3 2 1 0 0 0 1 1 3 0 0 0 0 0 4 4 0 0 0 0 1 5 5 0 1 1 0 0 • Diagonal entries are zero. • Adjacency matrix of a digraph need not be symmetric.

Adjacency Matrix  n2 bits of space  For an undirected graph, may store only lower or upper triangle (exclude diagonal).  (n-1)n/2 bits  O(n) time to find vertex degree and/or vertices adjacent to a given vertex.

Adjacency Lists  Adjacency list for vertex i is a linear list of vertices adjacent from vertex i.  An array of n adjacency lists. aList[1] = (2,4) aList[2] = (1,5) aList[3] = (5) 2 3 aList[4] = (5,1) 1 aList[5] = (2,4,3) 4 5

Linked Adjacency Lists  Each adjacency list is a chain. 2 aList[1] 2 4 3 [2] 1 5 [3] 5 1 [4] 5 1 4 aList[5] 2 4 3 5 Array Length = n # of chain nodes = 2e (undirected graph) # of chain nodes = e (digraph)

Array Adjacency Lists  Each adjacency list is an array list. 2 aList[1] 2 4 3 [2] 1 5 [3] 5 1 [4] 5 1 4 aList[5] 2 4 3 5 Array Length = n # of list elements = 2e (undirected graph) # of list elements = e (digraph)

Weighted Graphs  Cost adjacency matrix.  C(i,j) = cost of edge (i,j)  Adjacency lists => each list element is a pair (adjacent vertex, edge weight)

Graph Search Methods • A vertex u is reachable from vertex v iff there is a path from v to u. 2 3 8 1 4 5 9 10 6 7 11

Graph Search Methods • A search method starts at a given vertex v and visits/labels/marks every vertex that is reachable from v. 2 3 8 1 4 5 9 1 0 6 7 11

Graph Search Methods • Many graph problems solved using a search method.  Path from one vertex to another.  Is the graph connected?  Find a spanning tree.  Etc. • Commonly used search methods:  Breadth-first search.  Depth-first search.