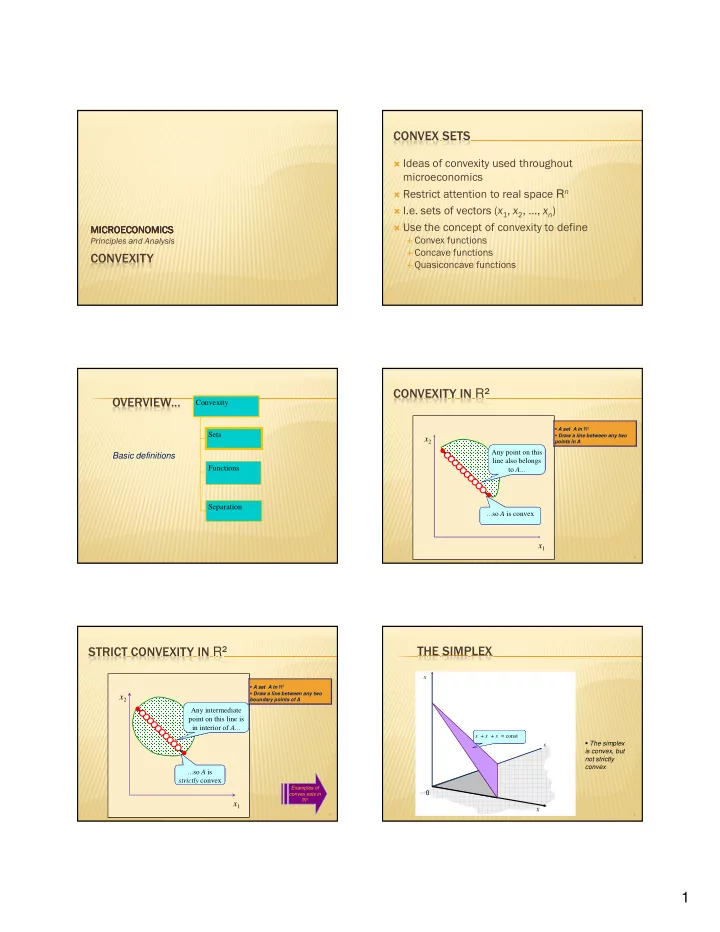

����������� � ����������������������������������� �������������� � ��������������������������������� R � � ���������������������� � !� � " !����!� � � #� � $������������������������������������� �������������� �������������� �������������� �������������� � ���������������� ����������������������� � ����������������� ��������� � %��������������������� 1 2 ������������� R � ����������� Convexity � A set A in R 2 Sets � Draw a line between any two x 2 points in A � Any point on this Basic definitions line also belongs Functions to A ... � Separation ...so A is convex x 1 3 4 ����������� �������������������� R � x 1 � A set A in R 2 � Draw a line between any two x 2 boundary points of A � Any intermediate point on this line is in interior of A ... x 1 + x 2 + x 3 = const � The simplex � is convex, but not strictly convex ...so A is strictly convex Examples of 0 convex sets in R 3 x 1 x 3 5 6 1
�������� ����������� Convexity x 1 Sets For scalars and � A ball centred on Σ i [ x i – a i ] 2 = const vectors the point ( a 1 , a 2 , a 3 ) Functions > 0 � It is strictly convex Separation 0 x 3 8 7 ���������������� ��������������������� � A function f: R � R � A function f: R � R y � Draw A, the set "above" the � Draw the function –f function f y � Draw A, the set "above" the y = f ( x ) function –f A := {( x , y ): y � f ( x )} � If A is convex, f is a � If –f is a convex function, convex function f is a concave function x y = f ( x ) � If A is strictly convex, f � Equivalently, if the set is a strictly convex "below" f is convex, f is a function concave function x � If –f is a strictly convex function, f is a strictly concave function 9 10 ��������������������� ��������������������������� y � A function f: R 2 � R � An affine function f: R � R y = f ( x ) y y = f ( x ) � Draw the set "above" the � Draw the set "below" the function f function f � Draw the set "below" the function f � The graph in R 2 is a straight line. � Set "below" f is � Both "above" and “below" strictly convex, x sets are convex. x 2 so f is a strictly 0 concave function � So f is both concave and convex. � Corresponding graph in R 3 would be a plane. � The graph in R n would be a hyperplane. 11 12 2
�������������� �������������� � ��������������!���� ����������� ����������� �������������� ����������� ����������� ����&������������������������������������������ ��������������'�������������������������������� If instead ������������������������������������������������� ������������� for any and � �(����������!�������������������������������� , then f is strictly quasiconvex . ��'���� � ��������������������������(����������� ���)��������� ����� ���� 13 14 �������������� ����������������������� � *�(�����������������������������������)����� � *�(��������������������)������������������� ������������(����������!���������������� (�����������������������������������)����� ���������������������(����������� � *����������#�(���������������������������������#� ���������)���������������!�)����������������#� (����������������������������������#�������� ������������������� 15 16 ����������������������� �������������� � *����������)������������(����������+���������������������������������������� x 2 �������������)�����������������������������'���)���������������������������� � Draw contours of a function f: R 2 � R ��������������)���������������!�)������������������������� � Pick the contour for some specific y-value y 0 . � Draw the "better-than" set for y 0 . � If the "better-than" set B ( y 0 ) B ( y 0 ) is convex, f is a concave-contoured function � An equivalent term is a "quasiconcave" function � If B ( y 0 ) is strictly convex, f y 0 = f ( x ) is a strictly quasiconcave" x 1 function 17 18 3
������������������������ ����������� Convexity convex � Two convex sets in R 2 Sets � Convex and nonconvex sets � Convex sets can be separated by a hyperplane... Fundamental � ...but nonconvex sets sometimes can't be separated relations Functions non-convex convex Separation convex 19 20 ���������������� R � ������������������������ � ����� � � � x 2 � Hyperplane in R 2 is a straight � A convex set A H line � A point y "outside" A x 2 { x : Σ i p i x i � c } � Parameters p and c determine � The point x* in A that is closest the slope and position � y to y � Draw in points "above" H � The separating hyperplane � Draw in points "below" H � A x* � y � A. � y lies in the "above-H" set � x* lies in the "below-H" { x : Σ i p i x i � c } set x 1 x 1 21 22 �������������������������������� ��������������������� � Convex sets A and B. � Convex sets A and B. � A and B only have no points in � A and B only have boundary common. points in common. H H � The separating hyperplane. � The supporting hyperplane. A A � All points of A lie � Interior points of A lie � strictly above H strictly above H � All points of B lie � Interior points of B lie B B strictly below H strictly below H 23 24 4
Recommend
More recommend