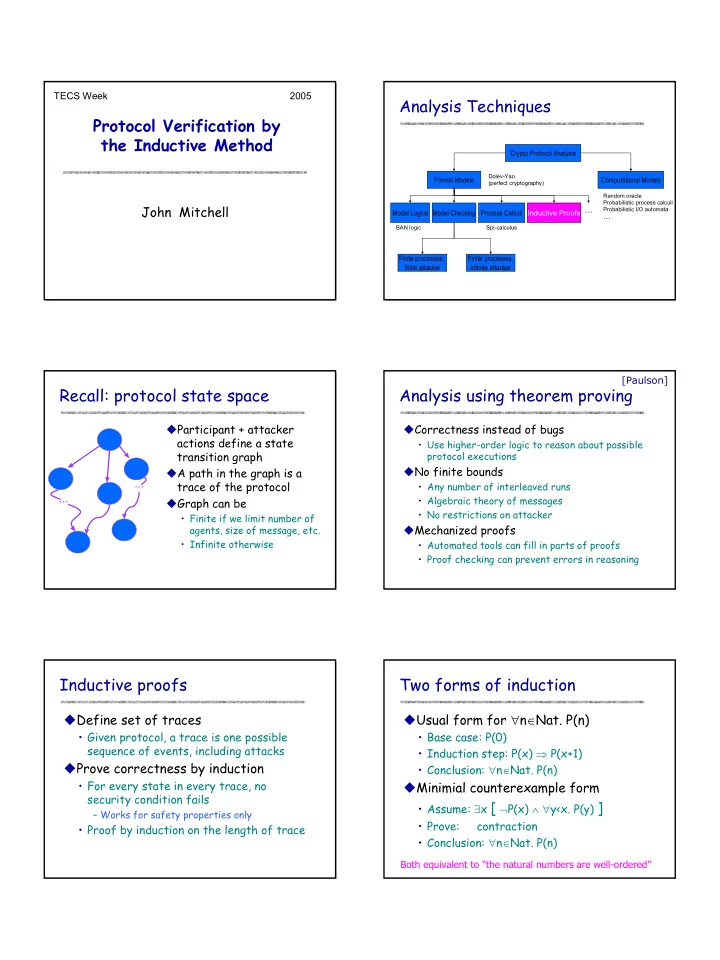

TECS Week 2005 Analysis Techniques Protocol Verification by the Inductive Method Crypto Protocol Analysis Dolev-Yao Formal Models Computational Models (perfect cryptography) Random oracle Probabilistic process calculi John Mitchell … Probabilistic I/O automata Modal Logics Model Checking Process Calculi Inductive Proofs … BAN logic Spi-calculus Finite processes, Finite processes, finite attacker infinite attacker [Paulson] Recall: protocol state space Analysis using theorem proving � Participant + attacker � Correctness instead of bugs actions define a state • Use higher-order logic to reason about possible transition graph protocol executions � No finite bounds � A path in the graph is a ... trace of the protocol • Any number of interleaved runs ... • Algebraic theory of messages � Graph can be • No restrictions on attacker • Finite if we limit number of � Mechanized proofs agents, size of message, etc. • Infinite otherwise • Automated tools can fill in parts of proofs • Proof checking can prevent errors in reasoning Inductive proofs Two forms of induction � Define set of traces � Usual form for ∀ n ∈ Nat. P(n) • Given protocol, a trace is one possible • Base case: P(0) sequence of events, including attacks • Induction step: P(x) ⇒ P(x+1) � Prove correctness by induction • Conclusion: ∀ n ∈ Nat. P(n) • For every state in every trace, no � Minimial counterexample form security condition fails • Assume: ∃ x [ ¬ P(x) ∧ ∀ y<x. P(y) ] – Works for safety properties only • Prove: contraction • Proof by induction on the length of trace • Conclusion: ∀ n ∈ Nat. P(n) Both equivalent to “the natural numbers are well-ordered” 1
Use second form Sample Protocol Goals � Given set of traces � Authenticity: who sent it? • Fails if A receives message from B but thinks it • Choose shortest sequence to bad state is from C • Assume all steps before that OK � Integrity: has it been altered? • Derive contradiction • Fails if A receives message from B but message is not what B sent – Consider all possible steps � Secrecy: who can receive it? • Fails if attacker knows message that should be secret � Anonymity • Fails if attacker or B knows action done by A These are all safety properties All states are good Bad state Inductive Method in a Nutshell Work by Larry Paulson � Isabelle theorem prover • General tool; protocol work since 1997 Informal Correctness Attacker Abstract � Papers describing method Protocol theorem inference trace model Description about traces rules � Many case studies same for all protocols! • Verification of SET protocol (6 papers) • Kerberos (3 papers) • TLS protocol Theorem Try to prove is correct • Yahalom protocol, smart cards, etc the theorem http://www.cl.cam.ac.uk/users/lcp/papers/protocols.html Isabelle � Automated support for proof development • Higher-order logic • Serves as a logical framework • Supports ZF set theory & HOL • Generic treatment of inference rules � Powerful simplifier & classical reasoner � Strong support for inductive definitions 2
Agents and Messages Protocol semantics agent A , B ,… = Server | Friend i | Spy � Traces of events: msg X , Y ,… = Agent A • A sends X to B � Operational model of agents | Nonce N � Algebraic theory of messages (derived) | Key K � A general attacker | { X , Y } � Proofs mechanized using Isabelle/HOL | Crypt X K Typed, free term algebra, … Define sets inductively Protocol events in trace � Traces � Several forms of events • Set of sequences of events • A sends B message X • Inductive definition involves implications • A receives X if ev 1 , …, ev n ∈ evs, then add ev’ to evs • A stores X � Information from a set of messages A → B {A,N A } pk(B) If ev is a trace and Na is unused, add • parts H : parts of messages in H Says A B Crypt(pk B){A,Na} • analz H : information derivable from H If Says A’ B Crypt(pk B){A,X} ∈ ev B → A {N B ,N A } pk(A) and Nb is unused, add • synth H : msgs constructible from H Says B A Crypt(pk A){Nb,X} A → B {N B } pk(B) If Says ...{X,Na}... ∈ ev , add Says A B Crypt(pk B){X} Dolev-Yao Attacker Model Attacker Capabilities: Analysis � Attacker is a nondeterministic process analz H is what attacker can learn from H � Attacker can • Intercept any message, decompose into parts X ∈ H ⇒ X ∈ analz H • Decrypt if it knows the correct key { X , Y } ∈ analz H X ∈ analz H ⇒ • Create new message from data it has observed { X , Y } ∈ analz H Y ∈ analz H ⇒ � Attacker cannot Crypt X K ∈ analz H • Gain partial knowledge K -1 ∈ analz H • Perform statistical tests & X ∈ analz H ⇒ • Stage timing attacks, … 3
Attacker Capabilities: Synthesis Equations and implications analz(analz H ) = analz H synth H is what attacker can create from H synth(synth H ) = synth H infinite set! analz(synth H ) = analz H ∪ synth H synth(analz H ) = ??? X ∈ H X ∈ synth H ⇒ X ∈ synth H & Y ∈ synth H { X , Y } ∈ synth H ⇒ Nonce N ∈ synth H ⇒ Nonce N ∈ H X ∈ synth H & K ∈ synth H Crypt K X ∈ synth H Crypt K X ∈ H ⇒ Crypt X K ∈ synth H ⇒ or X ∈ synth H & K ∈ H Inductive Method: Pros & Cons Attacker and correctness conditions � Advantages If X ∈ synth(analz(spies evs )), • Reason about infinite runs, message spaces add Says Spy B X • Trace model close to protocol specification • Can “prove” protocol correct X is not secret because attacker can construct it from the parts it learned from events � Disadvantages If Says B A {N b ,X} pk(A) ∈ evs & • Does not always give an answer • Failure does not always yield an attack Says A’ B {N b } pk(B) ∈ evs , • Still trace-based properties only Then Says A B {N b } pk(B) ∈ evs • Labor intensive – Must be comfortable with higher-order logic If B thinks he’s talking to A, then A must think she’s talking to B Caveat � Quote from Paulson (J Computer Security, 2000) The Inductive Approach to Verifying Cryptographic Protocols • The attack on the recursive protocol [40] is a sobering reminder of the limitations of formal methods… Making the model more detailed makes reasoning harder and, eventually, infeasible. A compositional approach seems necessary � Reference • [40] P.Y.A. Ryan and S.A. Schneider, An attack on a recursive authentication protocol: A cautionary tale. Information Processing Letters 65, 1 (January 1998) pp 7 – 10. 4
Recommend
More recommend