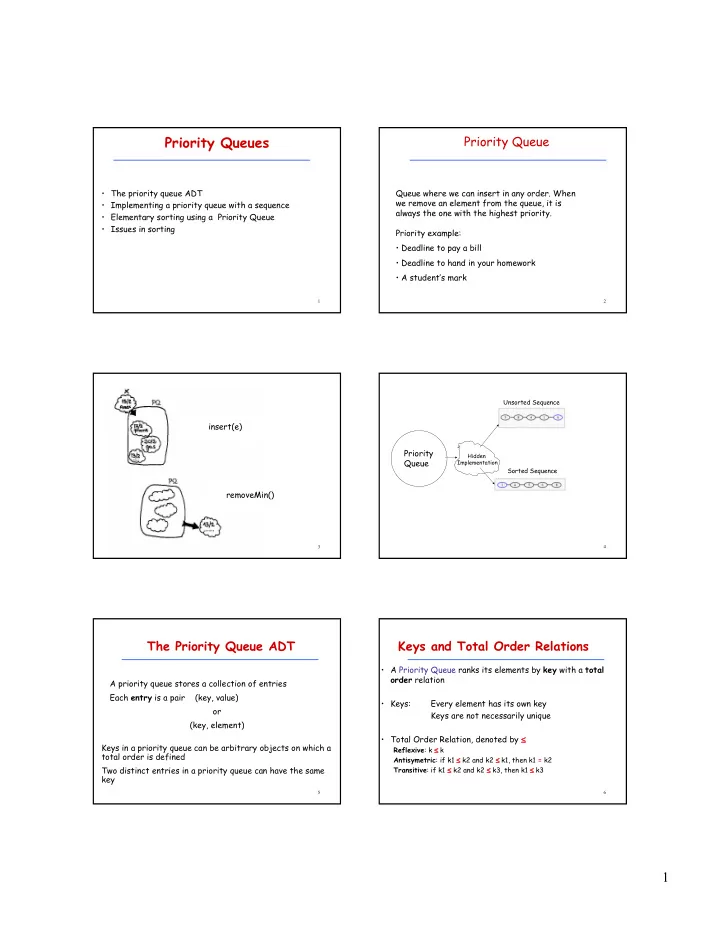

��������������� Priority�Queue � ���������������������� ��������������������������������������������� ��������������������� �������������!������� � ��������������������������������������������� ����������������������������������������� � ������������������������������������������ � ����������������� ����������"�����# � ������������������$��� � ��������������������������������% � ���������&�����% 1 2 Unsorted�Sequence ������'�( ��������� Hidden� ����� Implementation Sorted�Sequence ������)��'( 3 4 ���������������������� ������������������������������ � ���������������� ���%���������������$�� ��� ������� ������ ����� �������� �������������������������������������� �������� ����� ����� �������������'%��!������( � *���# ��������������������������%�� �� *������������������������������ '%��!��������( � ������,�����-�������!���������$�� ≤ ≤ ≤ ≤ *����������������������������$����$��������$+���������������� ��������� :�k� ≤ ≤ k ����������������� ���� ≤ ≤ ������������ :�if�k1� ≤ ≤ k2�and�k2� ≤ ≤ k1,�then�k1� � k2 ≤ ≤ ≤ ≤ ����������������������������������������������������������� ���������� :�if�k1� ≤ ≤ k2�and�k2� ≤ ≤ k3,�then�k1� ≤ ≤ k3 ≤ ≤ ≤ ≤ ≤ ≤ %�� 5 6 1
Total�ordering�examples But… • ��� are�not�total�orderings�since� • ≤ is�a�total�ordering they�are�not�reflexive� • ≥ is�also�a�total�ordering • Alphabetical�order:��we�define�a�≤ b�if�‘a’ is� • � is�not�a�total�ordering�since�we�can’t� before�‘b’ in�alphabetical�order compare�any�2�elements�with��=.� • Reverse�alphabetical�order Given�a,�b,�we�do�not�always�have� ��!����!�� 7 8 ���������������������� More�examples�of�ordering � �������������������������������� ����������������# We�can�order�the�co/ordinate�pairs .��/�'(# -�������������$���� �������������� p=(x 1 ,�y 1 )�and�q=(x 2 ,y 2 )�by .�������'(# ����������������������� .����������'%!�(#�������������������������������%���%������� 1.��p�≤ q if���x1�≤ x2 .����������'(# -������'$������&��������(������������� �� 2.�p≤ q�if y 1 ≤ y 2 ��������������%��0������������������� ����� ������ 3.�p≤ q�if���x1�≤ x2�and y 1 ≤ y 2 .���*��'(# -�������������������%�������0�������������������� � ����������� The�last�one�is�only�a�partial ordering! .������)��'(#�����-������ ��������������������������������� ���������������%��0���������������������������� ������������ 9 10 Entry�ADT� "��#���������� � ��������������������������$��� ����� ������������������ • An� ����� in�a�priority�queue�is�simply�a�key/ ��%�������� � ���#������ �$+����� value�pair � 2�����������$+����������"��������������%����������������$�� ��������������������������$+����� • Priority�queues�store�entries�to�allow�for� � ��������������������������$������������������������������ efficient�insertion�and�removal�based�on� �$+���� keys � ���������������������������# .��3�������'�!�$( • Methods: .��3�������,��������'�!$( 1 %��'(# ������������%��� ������������� .���������'�!�$( 1 �����'(# ��������������������������������������� .��4����������'�!$( ����� .��4����������,��������'�!$( .��2������$��'�( 11 12 2
Recommend
More recommend