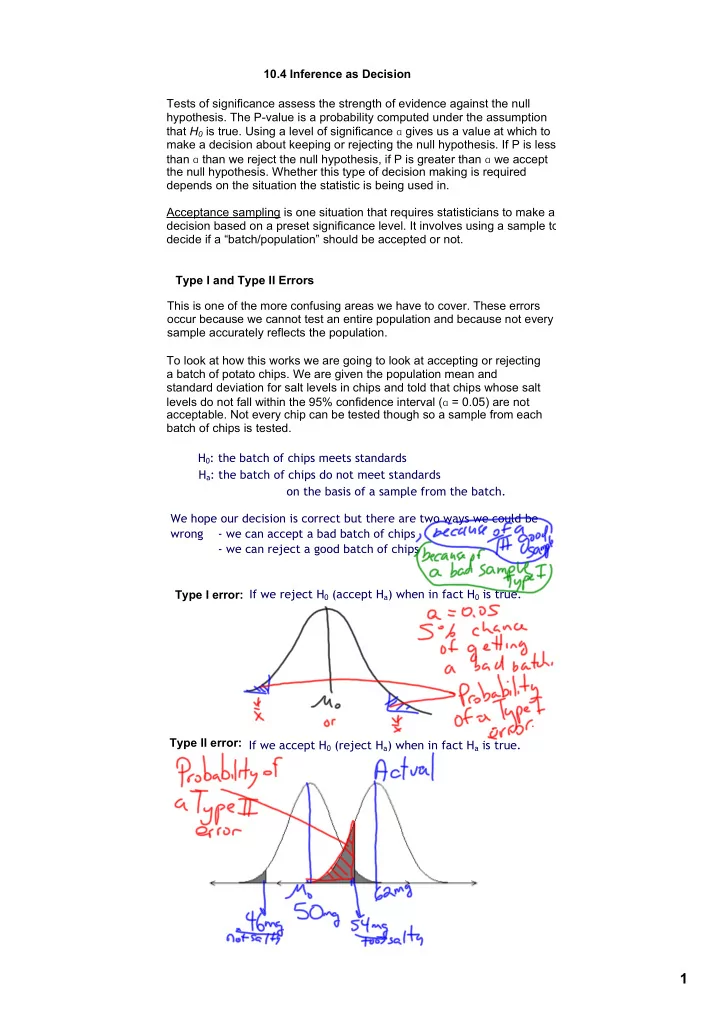

10.4 Inference as Decision Tests of significance assess the strength of evidence against the null hypothesis. The Pvalue is a probability computed under the assumption that H 0 is true. Using a level of significance ɑ gives us a value at which to make a decision about keeping or rejecting the null hypothesis. If P is less than ɑ than we reject the null hypothesis, if P is greater than ɑ we accept the null hypothesis. Whether this type of decision making is required depends on the situation the statistic is being used in. Acceptance sampling is one situation that requires statisticians to make a decision based on a preset significance level. It involves using a sample to decide if a “batch/population” should be accepted or not. Type I and Type II Errors This is one of the more confusing areas we have to cover. These errors occur because we cannot test an entire population and because not every sample accurately reflects the population. To look at how this works we are going to look at accepting or rejecting a batch of potato chips. We are given the population mean and standard deviation for salt levels in chips and told that chips whose salt levels do not fall within the 95% confidence interval ( ɑ = 0.05 ) are not acceptable. Not every chip can be tested though so a sample from each batch of chips is tested. H 0 : the batch of chips meets standards H a : the batch of chips do not meet standards on the basis of a sample from the batch. We hope our decision is correct but there are two ways we could be wrong ‐ we can accept a bad batch of chips ‐ we can reject a good batch of chips Type I error: If we reject H 0 (accept H a ) when in fact H 0 is true. Type II error: If we accept H 0 (reject H a ) when in fact H a is true. 1
Ex. 1 The mean salt content of a certain type of potato chips is supposed to be 2.0mg. The salt content of these chips varies normally with standard deviation σ=0.1mg. From each batch produced, an inspector takes a sample of 50 chips and measures the salt content of each chip. The inspector rejects the entire batch if the sample mean salt content is significantly different from 2mg at the 5% significance level. Calculate the probability of a type II error. Step 1: Write the rule for accepting H 0 in terms of x. Step 2: Find the probability of accepting H 0 assuming the alternative is true. 2
3
4
5
Recommend
More recommend