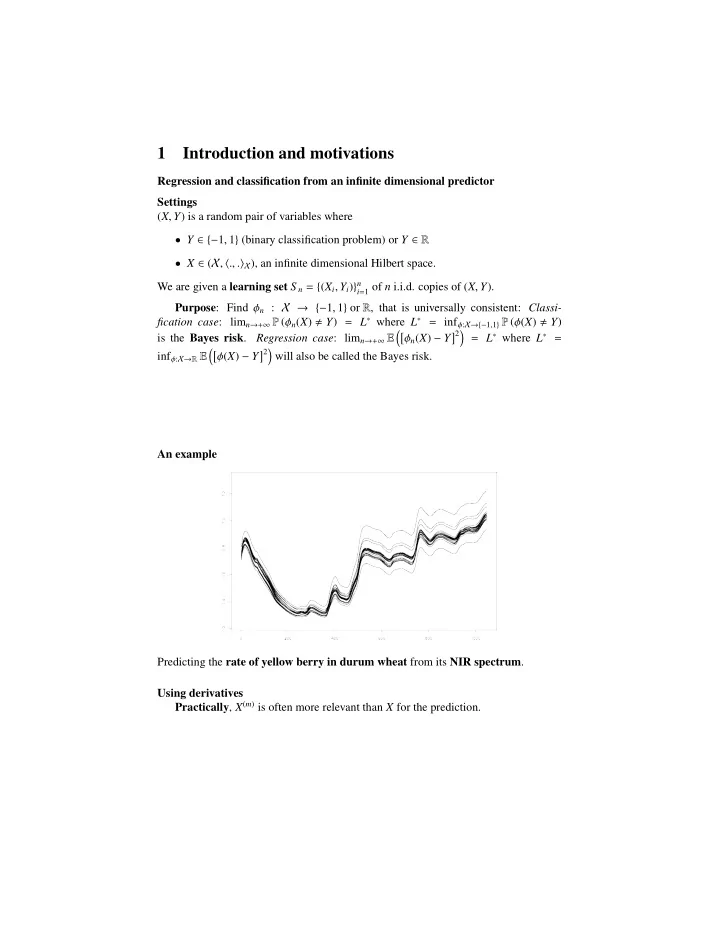
1 Introduction and motivations Regression and classification from - PDF document

1 Introduction and motivations Regression and classification from an infinite dimensional predictor Settings ( X , Y ) is a random pair of variables where • Y ∈ {− 1 , 1 } (binary classification problem) or Y ∈ R • X ∈ ( X , � ., . � X ), an infinite dimensional Hilbert space. We are given a learning set S n = { ( X i , Y i ) } n i = 1 of n i.i.d. copies of ( X , Y ). Purpose : Find φ n : X → {− 1 , 1 } or R , that is universally consistent: Classi- fication case : lim n → + ∞ P ( φ n ( X ) � Y ) = L ∗ where L ∗ = inf φ : X→{− 1 , 1 } P ( φ ( X ) � Y ) �� φ n ( X ) − Y � 2 � = L ∗ where L ∗ = is the Bayes risk . Regression case : lim n → + ∞ E �� φ ( X ) − Y � 2 � inf φ : X→ R E will also be called the Bayes risk. An example Predicting the rate of yellow berry in durum wheat from its NIR spectrum . Using derivatives Practically , X ( m ) is often more relevant than X for the prediction.

But X → X ( m ) induces information loss and � � φ : X→{− 1 , 1 } P ( φ ( X ) � Y ) = L ∗ φ ( X ( m ) ) � Y ≥ φ : D m X→{− 1 , 1 } P inf inf and �� � 2 � �� φ ( X ) − Y � 2 � = L ∗ . φ ( X ( m ) ) − Y ≥ φ : D m X→ R E inf φ : X→ R P inf 2

Sampled functions Practically , ( X i ) i are not perfectly known; only a discrete sampling is given: X τ d i = ( X i ( t )) t ∈ τ d where τ d = { t τ d 1 , . . . , t τ d | τ d | } . The sampling can be non uniform... ... and the data can be corrupted by noise. Then , X ( m ) is estimated from X τ d i , by � X ( m ) τ d , which also induces information loss : i � � � � φ ( � X ( m ) φ ( X ( m ) ) � Y ≥ L ∗ φ : D m X→{− 1 , 1 } P inf τ d ) � Y ≥ φ : D m X→{− 1 , 1 } P inf and �� � 2 � �� � 2 � φ ( � X ( m ) φ ( X ( m ) ) − Y ≥ L ∗ . φ : D m X→ R E inf τ d ) − Y ≥ φ : D m X→ R E inf 3

Purpose of the presentation Find a classifier or a regression function φ n ,τ d built from � X ( m ) τ d such that the risk of φ n ,τ d asymptotically reaches the Bayes risk L ∗ : � � φ n ,τ d ( � X ( m ) = L ∗ | τ d |→ + ∞ lim lim τ d ) � Y n → + ∞ P or �� � 2 � φ n ,τ d ( � = L ∗ X ( m ) τ d ) − Y | τ d |→ + ∞ lim lim n → + ∞ E Main idea : Use a relevant way to estimate X ( m ) from X τ d (by smoothing splines) and combine the consistency of splines with the consistency of a R | τ d | -classifier or re- gression function. 2 A general consistency result Basics about smoothing splines I Suppose that X is the Sobolev space � [0 , 1] |∀ j = 1 , . . . , m , D j h exists (weak sense) and D m h ∈ L 2 � H m = h ∈ L 2 equipped with the scalar product � m � u , v � H m = � D m u , D m v � L 2 + B j uB j v j = 1 where B are m boundary conditions such that Ker B ∩ P m − 1 = { 0 } . ( H m , � ., . � H m ) is a RKHS : ∃ k 0 : P m − 1 × P m − 1 → R and k 1 : Ker B × Ker B → R such that ∀ u ∈ P m − 1 , t ∈ [0 , 1] , � u , k 0 ( t , . ) � H m = u ( t ) and ∀ u ∈ Ker B , t ∈ [0 , 1] , � u , k 1 ( t , . ) � H m = u ( t ) See [Berlinet and Thomas-Agnan, 2004] for further details. 4

Basics about smoothing splines II A simple example of boundary conditions : h (0) = h (1) (0) = . . . = h ( m − 1) (0) = 0 . Then, � m − 1 t k s k k 0 ( s , t ) = ( k !) 2 k = 0 and � 1 ( t − w ) m − 1 ( s − w ) m − 1 + + k 1 ( s , t ) = dw . ( m − 1)! 0 Estimating the predictors with smoothing splines I Assumption (A1) • | τ d | ≥ m − 1 • sampling points are distinct in [0 , 1] • B j are linearly independent from h → h ( t ) for all t ∈ τ d x λ,τ d ∈ H m solution of [Kimeldorf and Wahba, 1971] : for x τ d in R | τ d | , ∃ !ˆ � � | τ d | 1 ( h ( t l ) − x τ d ) 2 + λ ( h ( m ) ( t )) 2 dt . arg min | τ d | h ∈H m [0 , 1] l = 1 x λ,τ d = S λ,τ d x τ d where S λ,τ d : R | τ d | → H m . and ˆ These assumptions are fullfilled by the previous simple example as long as 0 � τ d . Estimating the predictors with smoothing splines II S λ,τ d is given by: ω T ( U ( K 1 + λ I | τ d | ) U T ) − 1 U ( K 1 + λ I | τ d | ) − 1 S λ,τ d = + η T ( K 1 + λ I | τ d | ) − 1 ( I | τ d | − U T ( U ( K 1 + λ I | τ d | ) − 1 U ( K 1 + λ I | τ d | ) − 1 ) ω T M 0 + η T M 1 = with • { ω 1 , . . . , ω m } is a basis of P m − 1 , ω = ( ω 1 , . . . , ω m ) T and U = ( ω i ( t )) i = 1 ,..., m t ∈ τ d ; • η = ( k 1 ( t , . )) T t ∈ τ d and K 1 = ( k 1 ( t , t ′ )) t , t ′ ∈ τ d . The observations of the predictor X (NIR spectra) are then estimated from their sampling X τ d by � X λ,τ d . 5

Two important consequences 1. No information loss � � φ ( � φ : R | τ d | →{− 1 , 1 } P ( φ ( X τ d ) � Y ) φ : H m →{− 1 , 1 } P inf X λ,τ d ) � Y = inf and �� � 2 � �� φ ( X τ d ) − Y � 2 � φ ( � φ : H m →{− 1 , 1 } E inf X λ,τ d ) − Y = φ : R | τ d | →{− 1 , 1 } P inf 2. Easy way to use derivatives : ( Q λ,τ d u τ d ) T ( Q λ,τ d v τ d )( u τ d ) T M λ,τ d v τ d ( u τ d ) T M T 0 WM 0 v τ d + ( u τ d ) T M T 1 K 1 M 1 v τ d �S λ,τ d u τ d , S λ,τ d v τ d � H m � � u λ,τ d , � = v λ,τ d � u ( m ) v ( m ) ≃ � � λ,τ d , � λ,τ d � where K 1 , M 0 and M 1 have been previously defined and W = ( � ω i , ω j � H m ) i , j = 1 ,..., m . where M λ,τ d is symmetric, definite positive. where Q λ,τ d is the Choleski triangle of M λ,τ d : Q T λ,τ d Q λ,τ d = M λ,τ d . Remark : Q λ,τ d is calcu- lated only from the RKHS, λ and τ d : it does not depend on the data set. Classification and regression based on derivatives Suppose that we know a consistent classifier or regression function in R | τ d | that is based on R | τ d | scalar product or norm. The corresponding derivative based classifier or regression function is given by using the norm induced by Q λ,τ d : Example : Nonparametric kernel regression � � u − U i � R | τ d | � � n i = 1 T i K h n Ψ : u ∈ R | τ d | → � � u − U i � R | τ d | � � n i = 1 K h n 6

where ( U i , T i ) i = 1 ,..., n is a learning set in R | τ d | × R . � � Q λ,τ d x τ d − Q λ,τ d X � � n τ d i � R | τ d | i = 1 Y i K h n φ n , d = Ψ ◦ Q λ,τ d : x ∈ H m → � � Q λ,τ d x τ d − Q λ,τ d X � � n τ d i � R | τ d | i = 1 K h n � � � n � x ( m ) − X ( m ) � L 2 i = 1 Y i K i h n ≃ − → � � � n � x ( m ) − X ( m ) � L 2 i = 1 K i h n Remark for consistency Classification case (approximatively the same is true for regression): � � � � − L ∗ = P φ n ,τ d ( � φ n ,τ d ( � − L ∗ d + L ∗ d − L ∗ P X λ,τ d ) � Y X λ,τ d ) � Y where L ∗ d = inf φ : R | τ d | →{− 1 , 1 } P ( φ ( X τ d ) � Y ). 1. For all fixed d , � � φ n ,τ d ( � = L ∗ n → + ∞ P lim X λ,τ d ) � Y d as long as the R | τ d | -classifier is consistent because there is a one-to-one mapping between X τ d and � X λ,τ d . �� � � � � d − L ∗ ≤ E � � 2. L ∗ � E ( Y | � with consistency of spline estimate � X λ,τ d ) − E ( Y | X ) X λ,τ d and � assumption on the regularity of E ( Y | X = . ), consistency would be proved. But continuity of E ( Y | X = . ) is a strong assumption in infinite dimensional case, and is not easy to check. Spline consistency Let λ depends on d and denote ( λ d ) d the series of regularization parameters. Also introduce ∆ τ d : = max { t 1 , t 2 − t 1 , . . . , 1 − t | τ d | } , ∆ τ d : = min 1 ≤ i < | τ d | { t i + 1 − t i } Assumption (A2) • ∃ R such that ∆ τ d / ∆ τ d ≤ R for all d ; • lim d → + ∞ | τ d | = + ∞ ; • lim d → + ∞ λ d = 0. [Ragozin, 1983] : Under (A1) and (A2), ∃ A R , m and B R , m such that for any x ∈ H m and any λ d > 0, � � � � 1 � � d → + ∞ � 2 � D m x � 2 � ˆ x λ d ,τ d − x L 2 ≤ A R , m λ d + B R , m − − − − − → 0 L 2 | τ d | 2 m 7

Bayes risk consistency Assumption (A3a) � � � D m X � 2 is finite and Y ∈ {− 1 , 1 } . E L 2 or Assumption (A3b) τ d ⊂ τ d + 1 for all d and E ( Y 2 ) is finite. Under (A1)-(A3), lim d → + ∞ L ∗ d = L ∗ . Proof under assumption (A3a) Assumption (A3a) � � � D m X � 2 is finite and Y ∈ {− 1 , 1 } . E L 2 The proof is based on a result of [Faragó and Györfi, 1975] : For a pair of random variables ( X , Y ) taking their values in X × {− 1 , 1 } where X is an arbitrary metric space and for a series of functions T d : X → X such that d → + ∞ E ( δ ( T d ( X ) , X )) − − − − − → 0 then lim d → + ∞ inf φ : X→{− 1 , 1 } P ( φ ( T d ( X )) � Y ) = L ∗ . • T d is the spline estimate based on the sampling; • the inequality of [Ragozin, 1983] about this estimate is exactly the assumption of Farago and Gyorfi’s Theorem. Then the result follows. Proof under assumption (A3b) Assumption (A3b) τ d ⊂ τ d + 1 for all d and E ( Y 2 ) is finite. Under (A3b), ( E ( Y | � X λ d ,τ d )) d is a uniformly bounded martingale and thus converges for the L 1 -norm. Using the consistency of ( � X λ d ,τ d ) d to X ends the proof. 8