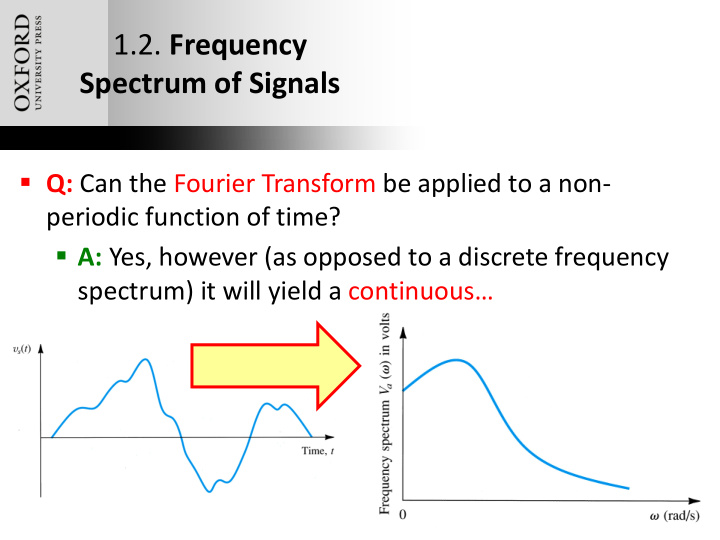



1.2. Frequency Spectrum of Signals § Q: Can the Fourier Transform be applied to a non- periodic function of time? § A: Yes, however (as opposed to a discrete frequency spectrum) it will yield a continuous… Oxford University Publishing Microelectronic Circuits by Adel S. Sedra and Kenneth C. Smith (0195323033)
1.4.5. Expressing Gain in Decibels § Q: How may gain be expressed in decibels ? = voltage gain in decibels 20 log A d B v = current gain in decibels 20 log A dB i = power gain in decibels 10 log ( A ) d B p Oxford University Publishing Microelectronic Circuits by Adel S. Sedra and Kenneth C. Smith (0195323033)
1.5.2. Cascaded Amplifiers § In real life, an amplifier is not ideal and will not have infinite input impedance or zero output impedance. § Cascading of amplifiers, however, may be used to emphasize desirable characteristics. § first amplifier – high R i , medium R o § last amplifier – medium R i , low R o § aggregate – high R i , low R o Oxford University Publishing Microelectronic Circuits by Adel S. Sedra and Kenneth C. Smith (0195323033)
1.6.1. Measuring the Amplifier Frequency Response § Q: How does one examine frequency response? § A: By applying sine-wave input of amplitude V i and frequency w . § Q: Why? § A: Because, although its amplitude and phase may change, its shape and frequency will not. this characteristic of sine wave applied to linear circuit is unique Oxford University Publishing Microelectronic Circuits by Adel S. Sedra and Kenneth C. Smith (0195323033)
1.6.1: Measuring the Amplifier Frequency Response input and output are similar for linear amplifier Oxford University Publishing Microelectronic Circuits by Adel S. Sedra and Kenneth C. Smith (0195323033)
1.6.1. Measuring the Amplifier Frequency Response § amplifier transfer function ( T ) – describes the input- output relationship of an amplifier – or other device – with respect to various parameters, including frequency of input applied. § It is a complex value, often defined in terms of magnitude and phase shift. V w = Ð w = f T ( ) and T ( ) o ! " #" $ V ! " #" $ i phase shift magnitude gain Oxford University Publishing Microelectronic Circuits by Adel S. Sedra and Kenneth C. Smith (0195323033)
1.6.2. Amplifier Bandwidth § Q: What is bandwidth of a device? § A: The range of frequencies over which its magnitude response is constant (within 3dB). § Q: For an amplifier, what is main bandwidth concern? § A: That the bandwidth extends beyond range of frequencies it is expected to amplify. Oxford University Publishing Microelectronic Circuits by Adel S. Sedra and Kenneth C. Smith (0195323033)
1.6.2. Amplifier Bandwidth Oxford University Publishing Microelectronic Circuits by Adel S. Sedra and Kenneth C. Smith (0195323033)
1.6.4. Single Time- Constant Networks § single time–constant (STC) network – is composed of (or may be reduced to) one reactive component and one resistance. § low pass filter – attenuates output at high frequencies, allow low to pass § high pass filter – attenuates output at low frequencies, allow high to pass § time constant ( t . ) – describes the length of time required for a network transient to settle from step change ( t = L / R = RC ) Oxford University Publishing Microelectronic Circuits by Adel S. Sedra and Kenneth C. Smith (0195323033)
1.6.4. Single Time- Constant Networks Figure 1.22: Two examples of STC § low pass filter (left) attenuates output at high s networks: (a) a low-pass network § high pass filter (right) and (b) a high-pass network. Oxford University Publishing Microelectronic Circuits by Adel S. Sedra and Kenneth C. Smith (0195323033)
1 1.6.4. Single Time- v Z w 1 j C Constant Networks = = µ low-pass: k o o 1 + w v Z Z + R i i o w j C v Z R = = µ w high-pass: k o o 1 + v Z Z + R i i o w j C Oxford University Publishing Microelectronic Circuits by Adel S. Sedra and Kenneth C. Smith (0195323033)
1.6.4. Single Time- Figure 1.2: Characteristics of Various STC Constant Networks low -pass high-pass K Ks transfer function + w + w 1 ( / s ) 1 0 0 transfer function K K + w w - w w (for physical freq.) 1 j ( / ) 1 j ( / ) 0 0 K K magnitude response + w w 2 + w w 2 1 j ( / ) 1 j ( / ) 0 0 - w w w w phase respon se tan ( / ) tan ( / ) 0 0 w = transmission at 0 K 0 w = ¥ transmission at 0 K 1 w = 3 db Frequency same 0 t Bode Plots refer to next slide Oxford University Publishing Microelectronic Circuits by Adel S. Sedra and Kenneth C. Smith (0195323033)
Figure: Low-Pass Filter Magnitude (top-left) and Phase (top-right) Responses as well as High-Pass Filter (bottom- left) and Phase (bottom-right) Responses Oxford University Publishing Microelectronic Circuits by Adel S. Sedra and Kenneth C. Smith (0195323033)
-20dB/decade drop, beginning -45 degrees/decade drop, from maximum gain at corner moving outward from -45 Figure: Low-Filter Magnitude (top-left) and Phase (top- frequency degree shift at corner frequency right) Responses as well as High-Pass Filter (bottom-left) and Phase (bottom-right) Responses -45 degrees/decade drop, +20dB/decade incline, until moving outward from +45 maximum gain is reached at degree shift at corner frequency corner frequency Oxford University Publishing Microelectronic Circuits by Adel S. Sedra and Kenneth C. Smith (0195323033)
Example 1.5: Voltage Amplifier § Examine voltage amplifier with: § input resistance ( R i ) § input capacitance ( C i ) § gain factor ( µ ) § output resistance ( R o ) § Q(a): Derive an expression for the amplifier voltage gain V o / V s as a function of frequency. From this, find expressions for the dc gain and 3 dB frequency. Oxford University Publishing Microelectronic Circuits by Adel S. Sedra and Kenneth C. Smith (0195323033)
Example 1.5: Voltage Amplifier Oxford University Publishing Microelectronic Circuits by Adel S. Sedra and Kenneth C. Smith (0195323033)
Example 1.5: Voltage Amplifier § Q(b): What is unity-gain frequency? How is it calculated? § A: Gain = 0 dB § A: It is known that the gain of a low-pass filter drops at 20dB per decade beginning at w 0 . Therefore unity gain will occur two decades past w 0 (40 dB – 20 dB – 20 dB ). § Q(c): Find v o ( t ) for each of the following input: v s = 0.1 sin (10 2 t ), v s = 0.1 sin (10 5 t ) Oxford University Publishing Microelectronic Circuits by Adel S. Sedra and Kenneth C. Smith (0195323033)
1.6.5. Classification of Amps Based on Frequency Response § internal capacitances – cause the falloff of gain at high frequencies § like those seen in previous example § coupling capacitors – cause the falloff of gain at low frequencies § are placed in between amplifier stages § generally chosen to be large Oxford University Publishing Microelectronic Circuits by Adel S. Sedra and Kenneth C. Smith (0195323033)
1.6.5. Classification of Amps Based on Frequency Response § directly coupled / dc amplifiers – allow passage of low frequencies § capacitively coupled amplifiers – allow passage of high frequencies § tuned amplifiers – allow passage of a “band” of frequencies Oxford University Publishing Microelectronic Circuits by Adel S. Sedra and Kenneth C. Smith (0195323033)
Recommend
More recommend