1 0 0 0
play

1 0 0 0 L x y 1 - PowerPoint PPT Presentation

Nov 29, 2022 •486 likes •546 views

cx Some key results on vectors and matrices 1 (cf. sections 2.2, 2.3 and supplement 2A) cx 2 x = c Multiplication by constant: x cx 1 n x Vector

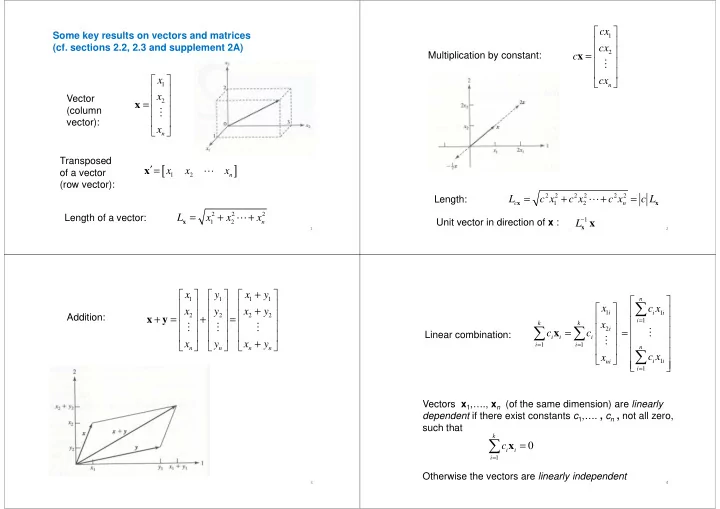
  1.  cx  Some key results on vectors and matrices 1   (cf. sections 2.2, 2.3 and supplement 2A) cx   2 x =  c Multiplication by constant:  ⋮    x  cx   1 n   x Vector   x 2 =   (column ⋮     vector): vector): x x     n Transposed [ ] ′= x x x x ⋯ of a vector 1 2 n (row vector): = 2 2 + 2 2 + 2 2 = L c x c x c x c L ⋯ Length: c x 1 2 n x 2 2 2 = + + L x x ⋯ x Length of a vector: Unit vector in direction of x : L − x x 1 x 1 2 n 1 2 +  x   y   x y  1 1 1 1  n  ∑        x  c x + x y x y   1 i i 1 i       2 2 2 2 x + y = + =   Addition:   i = 1 x       k k ⋮ ⋮ ⋮ ∑ ∑   x 2 i c = c =   ⋮       Linear combination: i i i   ⋮ x y x + y         = 1 = 1 i i   n n n n n ∑   c x x   1  i i  ni   = 1 i Vectors x 1 ,…., x n (of the same dimension) are linearly dependent if there exist constants c 1 ,…. , c n , not all zero, such that k ∑ x 0 = c i i = 1 i Otherwise the vectors are linearly independent 3 4

  2. x cos( ) θ = 1 Angle between vectors ( n = 2) 1 L Any set of n linearly independent vectors (of dimension n ) is x y a basis for the vector space, and every vector may be cos( ) θ = 1 2 L expressed as a unique linear combination of a given basis y x sin( ) θ = 2 1 L x Example with n = 4: y y sin( sin( ) ) θ θ = = 2 2 2 1 0 0 0 L  x          y 1           0 1 0 0 x           2 x = = + + + x x x x 1 2 3 4     0   0   1   0 x cos( ) cos( ) cos( )cos( ) sin( )sin( ) θ = θ − θ = θ θ + θ θ 3           2 1 2 1 2 1 0 0 0 1 x           4 y x y x x y + x y cos( ) θ = cos( θ − θ ) = ⋅ + ⋅ = 1 1 2 2 1 1 2 2 2 1 L L L L L L y x y x x y 5 6 x y ′ = + Inner product ( n = 2) x y x y Inner product (or dot product ) in general: 1 1 2 2 x y ′ = + + + x y x y ⋯ x y 1 1 2 2 n n = 2 + 2 = x x ′ L x x Length: x 1 2 + x y ′ x y x y ′ = 2 + 2 + 2 = x x L x x x cos( ) ⋯ θ = 1 1 2 2 = Length: Angle: x 1 2 n ′ ′ ′ ′ L L L L x x y y x x y y x y x y ′ x y ′ cos( ) θ = = Angle: ′ ′ L L x x y y Remember that cos(90 o ) = cos(270 o ) = 0 x y The vectors x and y are perpendicular if their inner The vectors x and y are perpendicular (or orthogonal ) product is zero if their inner product is zero 7 8

  3. Matrix of dimension n x p : Projection of a vector x on a vector y :  a a a  ⋯ 11 12 1 p   a a a ⋯   21 22 2 A p =  ′ ′ ′ y x y y x y x y  ⋮ ⋮ ⋱ ⋮ cos( ) y y L θ ⋅ = L ⋅ = ⋅ = x x   2 y y ′ L L L L L a a ⋯ a   y x y y y   n 1 n 2 np Transposed matrix of dimension p x n : Transposed matrix of dimension p x n :  a a ⋯ a  11 21 n 1   a a a ⋯   12 22 n 2 A ′ =   ⋮ ⋮ ⋱ ⋮   a a a ⋯     1 2 p p np Note: A column vector of dimension n is a n x 1 matrix A row vector dimension n is a 1 x n matrix 9 10 For a n x k matrix A and a k x p matrix B we have Multiplication by constant : the matrix product ca ca ca  ⋯   a a a   ⋯ 11 12 1 p 11 12 1 k b b b  ⋯ ⋯      11 1 1 j p ca ca ca ⋯ ⋮ ⋮ ⋮       21 22 2 p A =  b ⋯ b ⋯ b c  21 2 j 2 p  AB =   a a a ⋮ ⋮ ⋱ ⋮ ⋯ 1 2   i i ik ⋮ ⋮ ⋮      ca ca ⋯ ca ⋮ ⋮ ⋮         1 2 n n np b ⋯ b ⋯ b      k 1 kj kp a a a a a a ⋯ ⋯     1 1 2 2 n n n n nk nk Addition of matrices (of same dimension) : ∑ ∑ ∑   a b ⋯ a b ⋯ a b 1 l l 1 1 l lj 1 l lp l l l   ⋮ ⋮ ⋮   + + +  a b a b ⋯ a b  11 11 12 12 1 1 p p     ∑ ∑ ∑ =  a b ⋯ a b ⋯ a b + + + a b a b ⋯ a b  1   il l il lj il lp l l l 21 21 22 22 2 p 2 p A B + =     ⋮ ⋮ ⋱ ⋮ ⋮ ⋮ ⋮     ∑ ∑ ∑ a + b a + b a + b a b ⋯ a b ⋯ a b ⋯         1 1 2 2 1 n n n n np np nl l nl lj nl lp l l l 11 12

  4. For a n x k matrix A and a k x n matrix B we have The rank of matrix equals the maximum number of ( AB ) ′ B A ′ ′ = linearly independent columns (or rows) A k x k matrix A is nonsingular if the columns of A are linearly independent, i.e. if the matrix has rank k A matrix A of dimension k x k is a square matrix Let A be a nonsingular k x k matrix. Then there A = A ′ If we say that the matrix is symmetric exists a unique k x k matrix B such that AB = B A = I (the identity matrix) A The determinant of a k x k matrix A is denoted A − 1 B is the inverse of A and is denoted by For a 2 x 2 matrix we have For nonsingular square matrices A and B we have A = a a − a a 11 22 12 21 1 ′ ′ 1 ( A − ) = ( A ) − For k larger than 2 we may use computer software 1 1 1 ( AB ) − = B A − − 13 14 A k x k matrix A has eigenvalue λ with A k x k matrix Q is orthogonal if x 0 ≠ eigenvector if QQ ′ = Q Q ′ = I or Q ′ = Q − 1 Ax = λ x The columns of Q have unit length and are perpendicular An eigenvalue λ is a solution to the equation (and similarly for the rows) A I 0 − λ = Let A be a symmetric k x k matrix and x a k dimensional Let A be a symmetric k x k matrix and x a k dimensional vector A symmetric k x k matrix A has k pairs of eigenvalues k k = ∑∑ ′ x A x a x x is denoted a quadratic form ij i j λ , e λ , e λ , e … and eigenvectors: i = 1 j = 1 1 1 2 2 k k x A x ′ 0 A is nonnegative definite provided that for all x ≥ The eigenvectors can be chosen to have length 1 and be mutually perpendicular. ′ x 0 A is positive definite provided that for all ≠ x A x > 0 The eigenvectors are unique unless two or more eigenvalues are equal

  5. For a symmetric k x k matrix A we have the spectral decomposition A = λ e e ′ + λ e e ′ + + λ e e ′ ⋯ 1 1 1 2 2 2 k k k e e , , , e λ λ , , , λ … … Here are the eigenvalues and 1 2 1 2 k k are the associated perpendicular and normalized are the associated perpendicular and normalized eigenvectors (i.e. e e ′ 1 and e e ′ 0 for ) = = i ≠ j i i i j

Recommend

More recommend