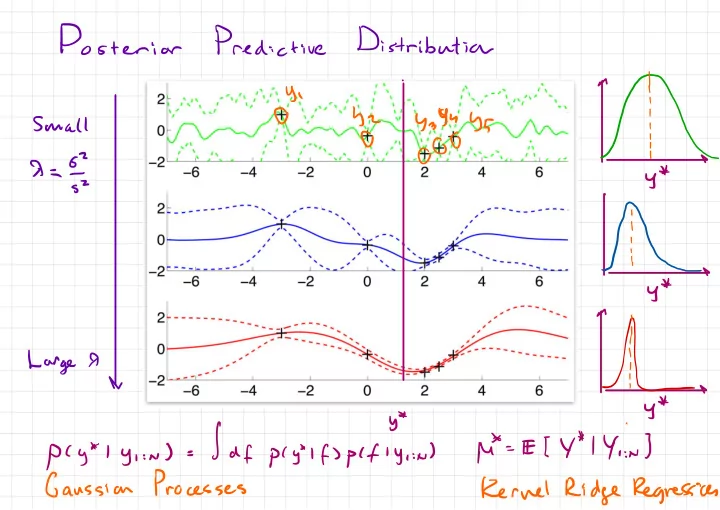

Posterior Predictive Distribution ,Y\ 00 @ hi 0 µ 1 . 5h45 , Y } QOO y yz , µ*=E[ be ya9uy5 Small 0 1 ' 7=5 , y* SZ ' 0 l o o co i , # y / 0 Large 0 oo0 A # y y* |df :b 4*14 ) P(y*ly :µ ) ) pcytlfspcfly , = :n , , Processes Gaussian Kernel Ridge Regression
/ Processes Gaussian Infinite Unbounded g Degrees freedom of Formal Nonparametric Distribution View Functions : on f 1 Y ) f p ( function Mean ~ ° flIn , :w × ) µ( function h( ) ... * • ' ) - Coviarana × ,× • . fcx ) • h ) . Prior functions F GPC µ ' ~ an YuIF=f~ . . , ( Norm ,6 ) ) Likelihood × - Likelihood prior Posterior ) p( y f) fly p( pcf ) 1 : = , :µ in , , pcyi ) :n / Marginal Evidence
Processes Gaussian Practical View : Generalization Multivariate Normal TIFIF of ) plfcx ) blini 1 =/ µn µ ( In ) i= £m÷ k( In ,Im ) fk ' 2) Nonmlpi E~ , Norm If ) ,o2I - * t.IE I x g*=KII 't split " piylfspc # f) DI Pc 15 f * Predictive ) : t 5) Pc
Distributions ( ¥* Joint µ×# Values Function an nleext ,yYI!,/ - Nonmllyu "¥ , ] ,KuYx¥xthuYx¥IH ) : "&%" she ? h , .nl =(µlIn , ) ) ,pkI uk ) , ... ,×*,= na taxes ,µ#n # M HKI , .si?l.....hlxInFn ) ... , Y E E + E hlx ,Xl ) µom(µx ) = - , Norm ( Mk ) 4- , kk ,X)tEI ) E 621 ) Norm ( ~ o ~ , hcx :o) ) hkx 't 's to Nonm( I ) - HKIH ' , .
Tf ) Normans Multivariate : Properties of Gaussian Probability for variables density jointly N M µ N×N µ NXM , lets ) ) Nonmflfililabt piers = M M MXM M×µ Marginal Conditional ftp.t.N/a;a+cB'lpi.bl.pCp)=Norm(p;5iB N NXMMXMM Norm # A) pH i. ) = pc ) A CB "Ct ) . MXMMXN NXM 14×14
Fla Distributions Values Function on ' =5 hiya Mk ys µK ) - o Predictive ) , ] pct*lF=j)= ;FK*hkKK* Can define l¥*]~N0nmlkµY¥ .MY#xxtt*huYxYIM ) .µ¢x 51=5 I* - Predictive function values new an µi(×)=o ) ) Normlt / hk ,*xl ( kk ,×l+iIYh µcx*s ) ) + = M m NXN Mxkl X ' hk ,# ,x+MIhH,x* ) hcxxixllhlx = + MXM MXM µxN µ×M MXN \
kernel Ridge Regression Yn ) 5=14 * ' f li ' ' ' ' ( k ' , Its , g + = ( In ,Im be Knm ) = ten lr ( I* In ) = ,
Gaussian Processes Kennel Ridge Regression vs Reformulation Kennel Ridge Regression of 's = &?wa¢ak fix it ( E. S Norm . ) = file 's ~ Norm ( 8,621 ) e- f (E) E 5 ~ = + lek 4tEilTS.4kj7-d@e0aKilSo.de ctekj ) ; ,I ;) = - Ft [ 4*15=5 ] h(x*,x ) ( ' +6215 hk ,x ) 5 = ( ) ) µKl=o Ridge Kernel Mean Regression GP Regression of c→
Large # Kennel Regularization Regression - based in @@8 HE ,Y\ 00 8 ooo µ ooo # @ l . 5h55 4 } y yz , be ya9uy5 Small 1 y* SZ ' 0 1 B D= 0 15.12 # y / 0 0 # y y* . fwnc ! absorbed Cov into kernel , Choice of { h( Ei ,I ;) ¢d( Ii ) So .de/0elEj ) implies function = choice of 9 e
Kernel Hyper parameters Choosing Rasmussen Carl Source : exp (-1×2*3) h( ' ) Squared Exponential x : x. = - l stronger Large regularization means
kernels Matern # inga Idea functions h times differentiable prior over : then Rainforth , PhD Thesis Tom Gamma , k=w - D - I 'll ) leu ( , }l÷g KfM2q ' ) E HE ,I 0=312,512 , 6 - = " .
Kernels Basis Duvenaud PhD David Source Thesis : ,
Combinations kernels of Duvenaud PhD David Source Thesis : , ' ) ' ) Sumi ,E I be ,( I. thzk h( In ,I = . ' ) hz( I ,I ' ) Product ,k I be ,( I. hl In : . =
Inner Products Definition twz Given It R vector : space over ( a) HxH→R function : a ; µ when it is product inner is an Linear 1 . ( f , , g) wzfz , g) µ < fz f , > ,g ( W w + = , , Symmetric 2 . ( g. f7µ ( f. g 7 µ = Positive definite 3 . ( f. f=o f) f. 2 f7µ iff o > , =o ,
, IF & map µEF Hilbert Spaces Kennels A H Definition vector equipped : space ( containing With product inner Cauchy an limit ) Hilbert Is sequences space a y not need be space ! vector A :4xX→R Definition function h Videos : document kernel function there is if numbers is a a , teeters f×,× H :X z Feature ¢ That such , → € ' ' )H Lax ) .dk . .= -
Infinite Sequences lz Definition ( summate ) sequences ; square all Wa ) ( that Such comprises W ÷ dz , as I War HWHE < as = , D= , lz ( loidk )d Given in ) sequence a , , ¢d :X R th coordinate where the → is d- := §|¢d(×)¢d( be ' ) 441,4k 'Dµ ( ' ( ) × ,x × =
Definiteness Positive Theorem If H Hibbert space is : a feature :X ¢ H is map → a . empty set ) ( X then and is a non be ( ¢ 1 y ) 7 µ { 4kt ,x' × 1 ÷ , positive definite is . ( . Anonsujn ) there For Theorem Moore : any ' ) definite h( positive is x. x Reproducing kernel Space ( RKHS ) Hibert unique a
Kernels Reproducing H Definition over that is Hilbert Suppose : space a then 71 :f→R functions f is a . RKHS ) kernel Hilbert ( When reproducing space 1. k( EH txeX x ) . , ( fl × ) ? fix ) hl ( Kernel ) . ) trick 2. . = , µ , ( Reproducing Property ) Implication ' )7µ=LkC h( ( ,x ) ,kl;× 'D K ' ) 441,4 x. × . =
Function Equivalence Classes Space Positive Reproducing Definite Kernels Functions Hilbert function spaces bounded with point evaluation
XOR Example Classic : 0 1 , , , " Xzo ' , - - . - . , , , I I I × , [ ¥z×z| Kennel hk.pt/#zaMy?l g.) Features dk ,xz)= ,
XOR Example Classic : = [ ¥g×z| otlxl Features 41517,3 hkijs . III. MY ;D Kennel ( ¢ki = - , = ( 8,4K¥ Functions fix }×i×z ) : = × W twzxz W + } , , , flit 2ft ) ,¢KDµ { in ,¢KDp } Rpnodnny = = Property kl . ,I ) ¢ # , =
Gaussian Processes Implications fan F. k ) GP( F . o ~ , h( ' I definite positive is x. x f lies RKHS → in F 15=5 k ) GPC Posterior ~ : picas kC¥×l( ,x)+iI5' kcx 5 = { mhlxsixnllhkixltttttnmym = . ,En ) pic )= kl { wn .
Recommend
More recommend