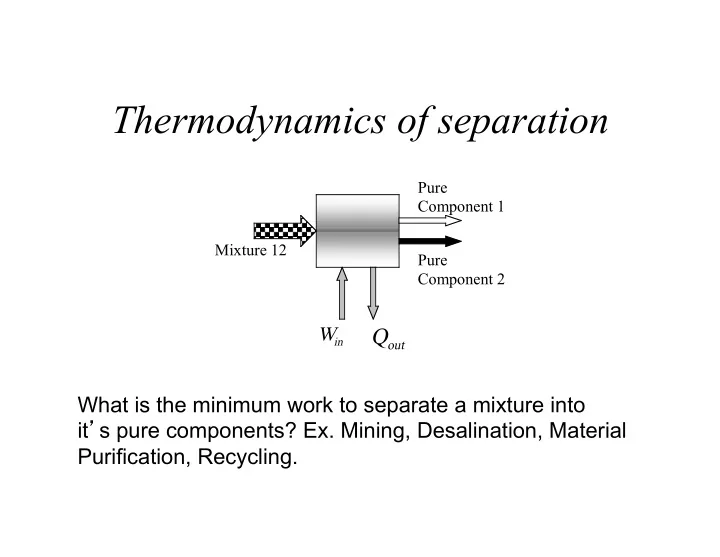

Thermodynamics of separation Pure Component 1 Mixture 12 Pure Component 2 W Q in out What is the minimum work to separate a mixture into it ’ s pure components? Ex. Mining, Desalination, Material Purification, Recycling.
Balance Eq ’ ns for Mass, Energy & Entropy dN i , sys = N i , in ! N i , out Pure dt Component 1 dE S irr dt = ! Q out + W in + H 12 ! H 1 ! H 2 Mixture 12 Pure Component 2 dS Q out + S 12 ! S 1 ! S 2 + S irr dt = ! W Q T 0 in out W in = (( H 1 + H 2 ) ! H 12 ) ! T o (( S 1 + S 2 ) ! S 12 ) + T o S irr W in = ! N 12 ( h mix ! T 0 s mix ) + T 0 S irr
Minimum Work of Separation W in = ! N 12 ( h mix ! T 0 s mix ) + T 0 S irr W in = ! mix + T 0 N 12 g o S irr W min = ! g # w min = mix N 12
Gibbs Free Energy of Mixing* mix – T 0 Δ s o Δ g o mix = Δ h o mix . mix ≈ – T 0 Δ s mix = Δ g o – T 0 ( s 12 – x 1 s 1 – x 2 s 2 ) For non-interacting molecules entropy can dominate often resulting in a negative Gibbs Free Energy and hence spontaneous mixing. I.e. Δ g o mix < 0 * at standard conditions
Boltzmann ’ s entropy equation S = k ln Ω n ! How many ways can “ r ” ! = atoms be positioned in r !( n r )! a lattice with “ n ” locations?
Ex. 4 atoms in 8 locations n ! 4!4! = 70 8! ! 12 = r !( n r )! = 1 w min = T 0 Δ s mix = k T 0 ( ln Ω 12 )
Using Stirling ’ s Approximation ln N! = N ln N - N w min = ! T 0 R ( x ln x + (1 ! x )ln(1 ! x )) Where x is mol fraction r/n , and R = k N avo
Multi-component System n ! ! = n 1 ! n 2 !..... n j ! j w min = ! T 0 R x i ln x i i = 1
“ Separation ” n w min = ! T 0 R x i ln x i i = 1
“ Extraction ” ( N ) W T R ( N ln ln x N ln( 1 x )) )) i = ! + ! 0 1 2 min min W N ( 1 ) ! T R (( N 1 ) ln x N ln( 1 x )) 1 = ! ! + ! min 0 1 2 w min, 1 = T 0 R (ln 1 ) x 1
Separation Examples • From the atmosphere • From the Ocean • Solutions – Polymer – Water based – Liquid metals (activity coef)
The minimum work to separate O 2 from the atmosphere Table from the EngineeringToolBox.com = T 0 R (ln 1 o e x , O 2 ) ! 298( K ) # 8.314( J / molK )ln(0.212) = 3.84( kJ / mol ) x O 2 In wet air you get 3.97 kJ/mol : compare with Szargut
kg (target) = kg (processed) Energy Energy i kg (target) kg (processed) ~ 1 Energy g i kg (processed)
energy requirements for mining and milling, possible future trends underground ~ 1000/g (MJ/t metal) open pit ~ 400/g (MJ/t metal) Chapman and Roberts p 113 & 116
Sherwood plot showing the relationship between the concentration of a target material in a feed stream and the market value of (or cost to remove) the target material [Grübler 1998].
Exergy of a Mixture e o e o ! ! x i x , i + RT x i ln x i x, mixture = x 0
Pure metal Exergy Metal alloy Recycle to Mixing in product pure metal Mixing in waste stream Pure ore (e.g. Fe 2 O 3 ) Further mixing and corrosion Ore value at mine CRUST at T o , p o Purification Stages Theoretical Exergy Values for a metal extracted from the earth ’ s crust shown at various stages of a product life cycle (not to scale)
Recommend
More recommend