Visual Encodings of Temporal Times are often imprecise The - PowerPoint PPT Presentation

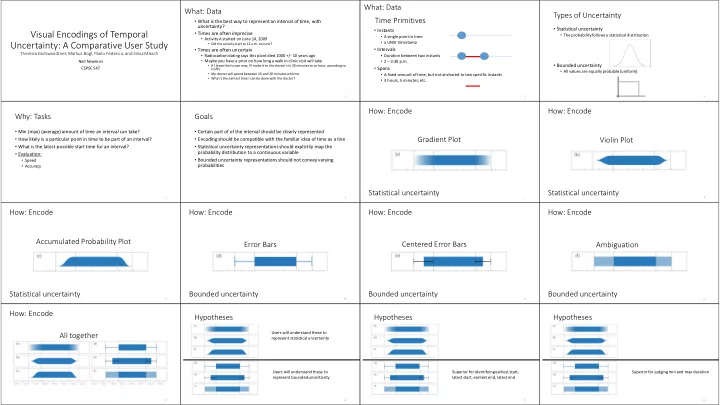
What: ¡Data What: ¡Data Types ¡of ¡Uncertainty Time ¡Primitives • What ¡is ¡the ¡best ¡way ¡to ¡represent ¡an ¡interval ¡of ¡time, ¡with ¡ uncertainty? • Statistical ¡uncertainty • Instants Visual ¡Encodings ¡of ¡Temporal ¡ • Times ¡are ¡often ¡imprecise • The ¡probability ¡follows ¡a ¡statistical ¡distribution • A ¡single ¡point ¡in ¡time • Activity ¡A ¡started ¡on ¡June ¡14, ¡2009 Uncertainty: ¡A ¡Comparative ¡User ¡Study • a ¡UNIX ¡timestamp • Did ¡the ¡activity ¡start ¡at ¡12 ¡a.m. ¡on ¡June? • Intervals • Times ¡are ¡often ¡uncertain TheresiaGschwandtner, ¡Markus ¡Bogl, ¡Paolo ¡Federico, ¡and ¡Silvia ¡Miksch • Radiocarbon ¡dating ¡says ¡this ¡plant ¡died ¡1000 ¡+/-­‑ 10 ¡years ¡ago • Duration ¡between ¡two ¡instants Neil ¡Newman • Maybe ¡you ¡have ¡a ¡prior ¡on ¡how ¡long ¡a ¡walk ¡in ¡clinic ¡visit ¡will ¡take • 2 ¡– 3:30 ¡p.m. ¡ • Bounded ¡uncertainty • If ¡I ¡leave ¡the ¡house ¡now, ¡I’ll ¡make ¡it ¡to ¡the ¡doctor’s ¡in ¡20 ¡minutes ¡to ¡an ¡hour, ¡according ¡to ¡ CSPSC ¡547 • Spans traffic • All ¡values ¡are ¡equally ¡probable ¡(uniform) • My ¡doctor ¡will ¡spend ¡between ¡10 ¡and ¡20 ¡minutes ¡with ¡me • A ¡fixed ¡amount ¡of ¡time, ¡but ¡not ¡anchored ¡to ¡two ¡specific ¡instants • What’s ¡the ¡earliest ¡time ¡I ¡can ¡be ¡done ¡with ¡the ¡doctor? ¡ • 3 ¡hours, ¡5 ¡minutes, ¡etc. 2 3 4 How: ¡Encode How: ¡Encode Why: ¡Tasks Goals • Min ¡(max) ¡(average) ¡amount ¡of ¡time ¡an ¡interval ¡can ¡take? • Certain ¡part ¡of ¡of ¡the ¡interval ¡should ¡be ¡clearly ¡represented Gradient ¡Plot Violin ¡Plot • How ¡likely ¡is ¡a ¡particular ¡point ¡in ¡time ¡to ¡be ¡part ¡of ¡an ¡interval? • Encoding ¡should ¡be ¡compatible ¡with ¡the ¡familiar ¡idea ¡of ¡time ¡as ¡a ¡line • What ¡is ¡the ¡latest ¡possible ¡start ¡time ¡for ¡an ¡interval? • Statistical ¡uncertainty ¡representations ¡should ¡explictily map ¡the ¡ probability ¡distribution ¡to ¡a ¡continuous ¡variable • Evaluation: • Bounded ¡uncertainty ¡representations ¡should ¡not ¡convey ¡varying ¡ • Speed probabilities • Accuracy Statistical ¡uncertainty Statistical ¡uncertainty 5 6 7 8 How: ¡Encode How: ¡Encode How: ¡Encode How: ¡Encode Accumulated ¡Probability ¡Plot Error ¡Bars Centered ¡Error ¡Bars Ambiguation Statistical ¡uncertainty Bounded ¡uncertainty Bounded ¡uncertainty Bounded ¡uncertainty 9 10 11 12 How: ¡Encode Hypotheses Hypotheses Hypotheses Users ¡will ¡understand ¡these ¡to ¡ All ¡together represent ¡statistical ¡uncertainty Users ¡will ¡understand ¡these ¡to ¡ Superior ¡for ¡identifying ¡earliest ¡start, ¡ Superior ¡for ¡judging ¡min ¡and ¡max ¡duration represent ¡bounded ¡uncertainty latest ¡start, ¡earliest ¡end, ¡latest ¡end 13 14 15 16

Hypotheses Hypotheses Data Participants • Generated ¡a ¡uniform ¡day, ¡month ¡in ¡2014 • 73 ¡Computer ¡Science ¡students, ¡taking ¡a ¡viz course Superior ¡for ¡judging ¡average ¡duration ¡of ¡ Equal ¡for ¡judging ¡probability ¡that ¡a ¡point ¡ • Randomly ¡add ¡/ ¡subtract ¡hours ¡to ¡get ¡start ¡times, ¡end ¡times • 14 ¡female interval falls ¡in ¡interval • Fixed ¡time ¡scale ¡for ¡all ¡visualizations • Normal ¡CDF ¡for ¡statistical ¡uncertainty 17 18 19 20 Tasks Tasks Tasks Tasks P(already_started) ¡= ¡? P(already_ended) ¡= ¡? ¡ (Repeated ¡for ¡each ¡of ¡the ¡3 ¡statistical ¡visualizations) Does ¡this ¡represent ¡statistical ¡or ¡bounded ¡uncertainty? ¡ Earliest ¡(Latest) ¡possible ¡start ¡(end)? ¡Min ¡(max) ¡(average) ¡duration? ¡ Preferences ¡(5 ¡point ¡scale) ¡for ¡each ¡viz (Repeated ¡for ¡each ¡of ¡the ¡6) (Repeated ¡for ¡each ¡of ¡the ¡6) 21 22 23 24 Hypotheses Hypotheses Experimental ¡Design ¡Flaws Users ¡will ¡understand ¡these ¡to ¡ • Earliest ¡start, ¡latest ¡start, ¡earliest ¡end, ¡latest ¡end ¡are ¡confusing ¡terms ¡ represent ¡statistical ¡uncertainty that ¡are ¡easy ¡to ¡mix ¡up • “The ¡probability ¡the ¡interval ¡has ¡already ¡ended” ¡is ¡1 ¡– “The ¡ probability ¡the ¡interval ¡is ¡ongoing” Users ¡will ¡understand ¡these ¡to ¡ Superior ¡for ¡identifying ¡earliest ¡start, ¡ represent ¡bounded ¡uncertainty latest ¡start, ¡earliest ¡end, ¡latest ¡end 25 26 27 28 Hypotheses Hypotheses Superior ¡(faster, ¡more ¡accurate) ¡for ¡ judging ¡average ¡duration ¡of ¡interval Superior ¡for ¡judging ¡min ¡and ¡max ¡duration 29 30 31 32

Hypotheses Preferences Equal ¡(speed, ¡accuracy) ¡for ¡judging ¡ probability ¡that ¡a ¡point ¡falls ¡in ¡interval 33 34 35 36 Criticisms Conclusions • Does ¡it ¡make ¡sense ¡to ¡compare ¡statistical ¡and ¡bounded ¡distributions ¡ • Compared ¡six ¡ways ¡of ¡encoding ¡temporal ¡uncertainty in ¡the ¡same ¡visualizations? ¡ • If ¡you ¡don’t ¡need ¡statistical ¡uncertainty, ¡any ¡of ¡the ¡three ¡bounded ¡ • Limited ¡scope ¡of ¡what ¡was ¡tested: ¡normal ¡distribution, ¡no ¡cases ¡ encodings ¡are ¡good where ¡the ¡certain ¡part ¡of ¡the ¡interval ¡is ¡shorter ¡than ¡it’s ¡starting ¡ • Gradient ¡plots ¡are ¡best ¡for ¡statistical ¡uncertainty uncertainty • Dependencies ¡between ¡intervals ¡were ¡not ¡explored 37 38