video 1 video 2 Point robot in a 2-dimensional workspace with - PDF document

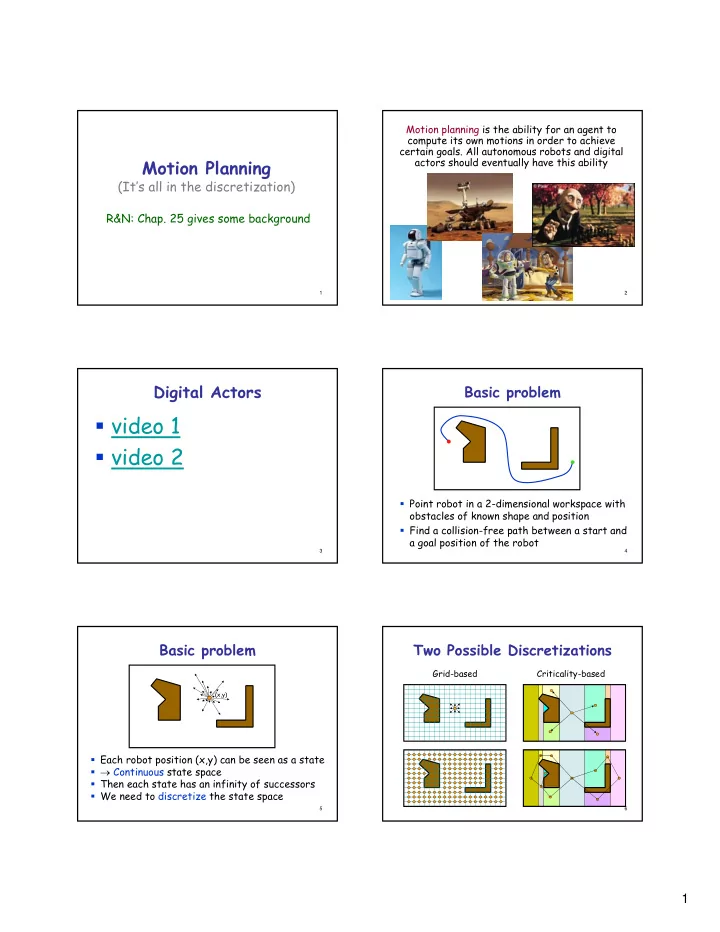
Motion planning is the ability for an agent to compute its own motions in order to achieve certain goals. All autonomous robots and digital Motion Planning actors should eventually have this ability (It’s all in the discretization) R&N: Chap. 25 gives some background 1 2 Digital Actors Basic problem � video 1 � video 2 � Point robot in a 2-dimensional workspace with obstacles of known shape and position � Find a collision-free path between a start and a goal position of the robot 3 4 Basic problem Two Possible Discretizations Grid-based Criticality-based (x,y) � Each robot position (x,y) can be seen as a state � → Continuous state space � Then each state has an infinity of successors � We need to discretize the state space 5 6 1

Two Possible Discretizations Intruder Finding Problem robot cleared region robot’s Grid-based Criticality-based visibility region hiding But this problem is very simple region 1 2 3 How do these discretizations scale up? 4 5 6 � A moving intruder is hiding in a 2-D workspace � The robot must “sweep” the workspace to find the intruder � Both the robot and the intruder are points 7 8 Information State Does a solution always exist? No ! a = 0 or 1 c = 0 or 1 b = 0 or 1 (x,y) 0 � cleared region 1 � hidding region � Example of an information state = (x,y,a=1,b=1,c=0) Easy to test: Hard to test: “Hole” in the workspace No “hole” in the workspace � An initial state is of the form (x,y,1, 1, ..., 1) � A goal state is any state of the form (x,y,0,0, ..., 0) 9 Criticality-Based Discretization Critical Line b=1 a=0 A E B C D b=1 b=0 a=0 a=0 Each of the regions A, B, C, D, and E consists of “equivalent” positions of the robot, Information state is unchanged so it’s sufficient to consider a single position Critical line per region 11 12 2

Criticality-Based Discretization Criticality-Based Discretization (C, 1, 1) (C, 1, 1) A A (B, 1) (D, 1) (B, 1) (D, 1) E E B C D B C D (C, 1, 0) (E, 1) 13 14 Criticality-Based Discretization Criticality-Based Discretization (C, 1, 1) (C, 1, 1) A A (B, 1) (D, 1) (B, 1) (D, 1) E E B C D B C D (C, 1, 0) (E, 1) (C, 1, 0) (E, 1) Much smaller search tree than (B, 0) (D, 1) (B, 0) (D, 1) with grid-based discretization ! 15 16 Grid-Based Discretization Example of Solution � Ignores critical lines � Visits many “equivalent” states � Many information states per grid point � Potentially very inefficient 17 18 3

Motion Planning for an But ... Articulated Robot Criticality-based discretization does not scale well in practice when the dimensionality of the continuous space increases (It becomes prohibitively complex to define and compute) Find a path to a goal configuration that satisfies various constraints: collision avoidance, equilibrium, etc... 19 20 Configuration Space of an How many dimensions has the Articulated Robot C-space of these 3 rings? � A configuration of a robot is a list of non-redundant parameters that fully specify the position and Answer: orientation of each of its 3 × 5 = 15 bodies � In this robot, one possible choice is: (q 1 , q 2 ) The configuration space (C-space) has 2 dimensions 21 22 ... and every robot path is a Every robot maps to a point in curve in C-space its C-space ... ~40 D 15 D 6 D 12 D q 0 q 1 q 0 q 1 q n q n q 3 q 3 ~65-120 D q 4 23 q 4 24 4

A robot path is a curve C-space “reduces” motion planning to in C-space finding a path for a point So, the C-space is the continuous state space of motion planning problems q 0 q 1 q n But how do the obstacle constraints map into C-space ? q 3 q 4 25 26 A Simple Example: Two-Joint Planar Robot Arm Continuous state space Discretization C-space Search Problems: • Geometric complexity • Space dimensionality 27 28 Robots with many joints: About Discretization Modular Self-Reconfigurable Robots � Dimensionality + geometric complexity Millipede-like robot with 13,000 joints � Criticality-based discretization turns out to be prohibitively complex � Dimensionality � Grid-based discretization leads to impractically large state spaces for dim(C-space) > 6 Each grid node has 3 n -1 neighbors, where n = dim(C-space) 29 30 (M. Yim) (S. Redon) 5

Probabilistic Roadmap (PRM) Probabilistic Roadmap (PRM) n -dimensional forbidden space feasible space Configurations are sampled by picking coordinates at random C-space 31 32 Probabilistic Roadmap (PRM) Probabilistic Roadmap (PRM) Configurations are sampled by picking coordinates at random Sampled configurations are tested for collision (feasibility) 33 34 Probabilistic Roadmap (PRM) Probabilistic Roadmap (PRM) The collision-free configurations are retained as “milestones” (states) Each milestone is linked by straight paths to its k-nearest neighbors 35 36 6

Probabilistic Roadmap (PRM) Probabilistic Roadmap (PRM) Each milestone is linked by straight paths to its k-nearest neighbors The collision-free links are retained to form the PRM (state graph) 37 38 Probabilistic Roadmap (PRM) Probabilistic Roadmap (PRM) The start and goal configurations are connected to nodes of the PRM The PRM is searched for a path from s to g g g s s 39 40 Why Does PRM Work? Continuous state space Because most feasible spaces verifies some good geometric (visibility) properties Discretization Search A* 41 42 7

Narrow-Passage Issue Why Does PRM Work? In most feasible spaces, every configuration “sees” a significant fraction of the feasible space The lookout of a subset S S 1 S 2 of the feasible space is the set of all configurations in S from which it is possible to “see” a significant fraction of the feasible space outside S Lookout of S 1 The feasible space is expansive if all of its subsets have a large � A relatively small number of milestones and connections between lookout them are sufficient to cover most feasible spaces with high probability 43 44 Probabilistic Completeness of a PRM Motion Planner In an expansive feasible space, the probability that a PRM planner with uniform sampling strategy finds a solution path, if one exists, goes to 1 exponentially with the number of milestones (~ running time) A PRM planner can’t detect that no path exists. Like A*, it must be allocated a time limit beyond which it returns that no path exists. But this answer may be incorrect . Perhaps the planner needed more time to find one ! 45 46 Sampling Strategies � Issue: Where to sample configurations? That is, which probabilistic distribution to use? � Example: Two-stage sampling strategy: 1. Construct initial PRM with uniform sampling 2. Identify milestones that have few connections to their close neighbors 3. Sample more configurations around them � Greater density of milestones in “difficult” regions of the feasible space 47 48 8

Collision Checking Hierarchical Collision Checking � Check whether objects overlap � Enclose objects into bounding volumes (spheres or boxes) � Check the bounding volumes 49 50 Hierarchical Collision Checking Hierarchical Collision Checking � Enclose objects into bounding volumes (spheres or boxes) � Enclose objects into bounding volumes (spheres or boxes) � Check the bounding volumes first � Check the bounding volumes first � Decompose an object into two � Decompose an object into two � Proceed hierarchically 51 52 Hierarchical Collision Checking Bounding Volume Hierarchy (BVH) � Enclose objects into bounding volumes (spheres or boxes) A BVH (~ balanced binary tree) is � Check the bounding volumes first pre-computed for each object � Decompose an object into two (obstacle, robot link) � Proceed hierarchically 53 54 9

Collision Checking BVH of a 3D Triangulated Cat Between Two Objects A A B C B C BVH of object 1 BVH of object 2 [Usually, the two trees have different sizes] � Search for a collision 55 56 Search for a Collision Search for a Collision Search tree Search tree AA AA Heuristic: Break pruning the largest BV A A A A 57 58 Search for a Collision Search for a Collision Search tree Search tree AA AA BA CA BA CA Heuristic: Break the largest BV CB CC B C C B A C 59 60 10

Search for a Collision Search Strategy � If there is no collision, all paths must eventually Search tree be followed down to pruning or a leaf node AA � But if there is collision, one may try to detect it as quickly as possible � � Greedy best-first search strategy with BA CA f(N) = h(N) = d/(r X +r Y ) [Expand the node XY CB CC r Y with largest relative d r X C overlap (most likely to Y B If two leaves of the BVH’s overlap contain a collision)] X (here, C and B) check their content C for collision B 61 62 Fortunately, hierarchical collision checkers are quite fast So, to discretize the state space of a motion On average, over 10,000 collision checks per planning problem, a PRM planner performs second for two 3-D objects each described by thousands of auxiliary searches (sometimes 500,000 triangles, on a contemporary PC even more) to detect collisions ! Checks are much faster when the objects are But from an outsider’s point of view the either neatly separated ( � early pruning) or search of the PRM looks like the main search neatly overlapping ( � quick detection of collision) 63 64 Free-Climbing Robot LEMUR IIb robot (created by NASA/JPL) 65 66 11