Use of parallel matrix algorithms for Laplace partial differential - PDF document

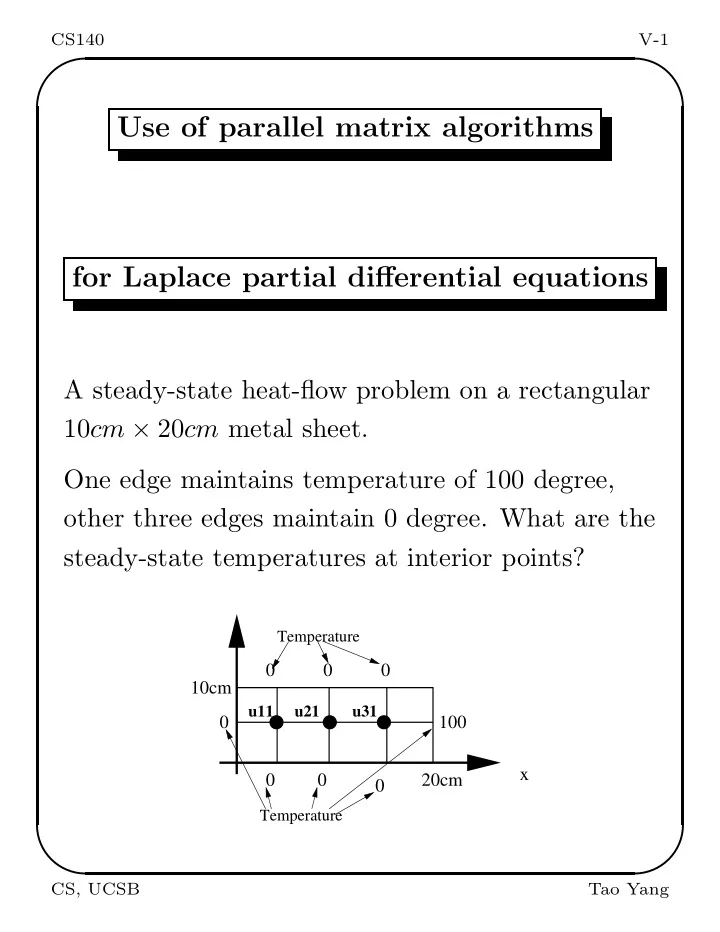
✬ ✩ CS140 V-1 Use of parallel matrix algorithms for Laplace partial differential equations A steady-state heat-flow problem on a rectangular 10 cm × 20 cm metal sheet. One edge maintains temperature of 100 degree, other three edges maintain 0 degree. What are the steady-state temperatures at interior points? Temperature 0 0 0 10cm u11 u21 u31 0 100 x 0 0 20cm 0 Temperature ✫ ✪ CS, UCSB Tao Yang

✬ ✩ CS140 V-2 The mathematical model Laplace equation: ∂ 2 U ( x, y ) + ∂ 2 u ( x, y ) = 0 ∂x 2 ∂y 2 with the boundary condition: u ( x, 0) = 0 , u ( x, 10) = 0 . u (0 , y ) = 0 , u (20 , y ) = 100 . Finite difference method to solve this PDE: • Discretize the region: Divide the function domain into a grid with gap h at each axis. • At each point ( ih, jh ), let u ( ih, jh ) = u i,j . Setup a linear equation using an approximated formula for numerical differentiation . • Solve the linear equations to find values of all points u i,j . ✫ ✪ CS, UCSB Tao Yang

✬ ✩ CS140 V-3 Approximating numerical differentiation f ′ ( x ) ≈ f ( x + h ) − f ( x ) or f ′ ( x ) ≈ f ( x ) − f ( x − h ) h h f ( x + h ) − f ( x ) + f ( x ) − f ( x − h ) f ′′ ( x ) ≈ f ′ ( x + h ) − f ′ ( x ) h h ≈ h h Thus f ′′ ( x ) ≈ f ( x + h ) + f ( x − h ) − 2 f ( x ) h 2 Then ∂ 2 u ( x i , y i ) ≈ u i +1 ,j − 2 u i,j + u i − 1 ,j ∂x 2 h 2 ∂ 2 u ( x i , y i ) ≈ u i,j +1 − 2 u i,j + u i,j − 1 ∂y 2 h 2 Adding the above two equations u i +1 ,j − 2 u ij + u i − 1 ,j + u i,j +1 − 2 u i,j + u i,j − 1 = 0 Then 4 u i,j − u i +1 ,j − u i − 1 ,j − u i,j +1 − u i,j − 1 = 0 ✫ ✪ CS, UCSB Tao Yang

✬ ✩ CS140 V-4 Example of Derived Linear Heat Equations Temperature 0 0 0 10cm u11 u21 u31 0 100 x 0 0 20cm 0 Temperature For this case: Let u 11 = x 1 , u 21 = x 2 , u 31 = x 3 . At u 11 , 4 x 1 − 0 − 0 − x 2 = 0 At u 21 , 4 x 2 − x 1 − 0 − x 3 − 0 = 0 At u 31 , 4 x 3 − x 2 − 0 − 100 − 0 = 0       4 − 1 0 x 1 0        = − 1 4 − 1 x 2 0                  0 − 1 4 x 3 100 Solutions: x 1 = 1 . 786 , x 2 = 7 . 143 , x 3 = 26 . 786 ✫ ✪ CS, UCSB Tao Yang

✬ ✩ CS140 V-5 Linear heat equations for a general 2D grid Given a general ( n + 2) × ( n + 2) grid, we have n 2 equations: 4 u i,j − u i +1 ,j − u i − 1 ,j − u i,j +1 − u i,j − 1 = 0 for 1 ≤ i, j ≤ n . Or express them as: u i,j = ( u i +1 ,j + u i − 1 ,j + u i,j +1 + u i,j − 1 ) / 4 Example, r = 2 , n = 6. Temperature held at U 0 Temperature Temperature held at U held at U1 0 Temperature held at U ✫ ✪ 0 CS, UCSB Tao Yang

✬ ✩ CS140 V-6 We order the unknowns as ( u 11 , u 12 , · · · , u 1 n , u 21 , u 22 , · · · , u 2 n , · · · , u n 1 , · · · , u nn ) For n = 2, the ordering is:     x 1 u 11         x 2 u 12     =         x 3 u 21             x 4 u 22 The matrix is:       4 − 1 − 1 0 x 1 u 01 + u 10             − 1 4 0 − 1 x 2 u 20 + u 31       =             − 1 0 4 − 1 x 3 u 02 + u 13                   0 − 1 − 1 4 x 4 u 32 + u 23 ✫ ✪ CS, UCSB Tao Yang

✬ ✩ CS140 V-7 In general, the left side matrix is:   T − I    − I T − I        − I T − I     ... ... ...         − I T n 2 × n 2   4 − 1    − 1 4 − 1        T = − 1 4 − 1     ... ... ...         − 1 4 n × n ✫ ✪ CS, UCSB Tao Yang

✬ ✩ CS140 V-8   1    1        I = 1     ...         1 n × n The matrix is too sparse, direct methods for solving this system takes too much time. ✫ ✪ CS, UCSB Tao Yang

✬ ✩ CS140 V-9 The Jacobi Iterative Method Given 4 u i,j − u i +1 ,j − u i − 1 ,j − u i,j +1 − u i,j − 1 = 0 for 1 ≤ i, j ≤ n . The Jacobi program: Repeat For i=1 to n For j=1 to n u new = 0 . 25( u i +1 ,j + u i − 1 ,j + u i,j +1 + u i,j − 1 ). i,j EndFor EndFor Until � u new − u ij � < ǫ ij Called 5-point stencil computation as u i,j depends on 4 neighbors. ✫ ✪ CS, UCSB Tao Yang

✬ ✩ CS140 V-10 The Gauss-Seidel Method Repeat u old = u . For i=1 to n For j=1 to n u i,j = 0 . 25( u i +1 ,j + u i − 1 ,j + u i,j +1 + u i,j − 1 ). EndFor EndFor Until � u ij − u old ij � < ǫ ✫ ✪ CS, UCSB Tao Yang

✬ ✩ CS140 V-11 Parallel Jacobi Method Assume we have a mesh of n × n processors. Assign u i,j to processor p i,j . The SPMD Jacobi program at processor p i,j : Repeat Collect data from four neighbors: u i +1 ,j , u i − 1 ,j , u i,j +1 , u i,j − 1 from p i +1 ,j , p i − 1 ,j , p i,j +1 , p i,j − 1 . u new = 0 . 25( u i +1 ,j + u i − 1 ,j + u i,j +1 + u i,j − 1 ). i,j diff i,j = | u new − u ij | ij Do a global reduction to get the maximum of diff i,j as M . Until M < ǫ ✫ ✪ CS, UCSB Tao Yang

✬ ✩ CS140 V-12 Performance evaluation • Each computation step takes ω = 5 operations. • There are 4 communication messages to be received. Assume sequential receiving. Communication costs 4( α + β ). • Assume that the global reduction takes ( α + β ) log n . • The sequential time Seq = Kωn 2 where K is the number of steps. • Assume ω = 0 . 5 , β = 0 . 1 , α = 100 , n = 500 , p 2 = 2500. • The parallel time PT = K ( ω + (4 + log n )( α + β )) ω ∗ n 2 Speedup = ω + (4 + log n )( α + β ) ≈ 192 Efficiency = Speedup = 7 . 7% . n 2 ✫ ✪ CS, UCSB Tao Yang

✬ ✩ CS140 V-13 Grid partitioning • Reduce the number of processors. Increase the granularity of computations. • Map the n × n grid to processors using 2D block method. Assume a p × p mesh, γ = n p . Example, r = 2 , n = 6. Temperature held at U 0 Temperature Temperature held at U held at U1 0 Temperature held at U 0 ✫ ✪ CS, UCSB Tao Yang

✬ ✩ CS140 V-14 Code partitioning Re-write the kernel part of the sequential code as: For bi = 1 to p For bj = 1 to p For i = ( b i − 1) γ + 1 to b i γ For j = ( b j − 1) γ + 1 to b j γ u new = 0 . 25( u i +1 ,j + u i − 1 ,j + u i,j +1 + u i,j − 1 ). i,j EndFor EndFor EndFor EndFor ✫ ✪ CS, UCSB Tao Yang

✬ ✩ CS140 V-15 Parallel SPMD code On processor p b i ,b j : Repeat Collect the data from its four neighbors. For i = ( b i − 1) γ + 1 to b i γ For j = ( b j − 1) γ + 1 to b j γ u new = 0 . 25( u i +1 ,j + u i − 1 ,j + u i,j +1 + u i,j − 1 ). i,j EndFor EndFor Compute the local maximum diff b i ,b j for the difference between old values and new values. Do a global reduction to get the maximum diff b i ,b j as M . Until M < ǫ ✫ ✪ CS, UCSB Tao Yang

✬ ✩ CS140 V-16 Performance evaluation • At each processor, each computation step takes ωr 2 operations. • The communication cost is 4( α + rβ ). • Assume that the global reduction takes ( α + β ) log p . • The number of steps is K . • Assume ω = 0 . 5 , β = 0 . 1 , α = 100 , n = 500 , r = 100 , p 2 = 25. PT = K ( r 2 ω + (4 + log p )( α + rβ )) ωr 2 p 2 Speedup = r 2 ω + (4 + log p )( α + rβ ) ≈ 21 . 2 . Efficiency = 84% . ✫ ✪ CS, UCSB Tao Yang