Unit 7 Fundamental Digital Building Blocks: Decoders & - PowerPoint PPT Presentation

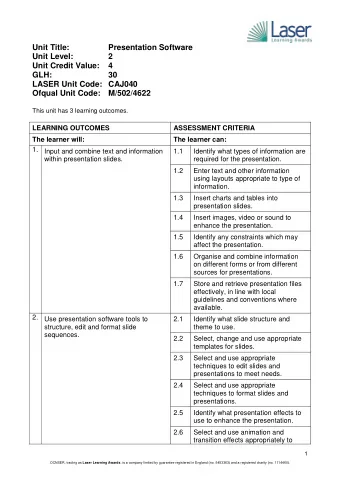
7.1 Unit 7 Fundamental Digital Building Blocks: Decoders & Multiplexers

7.2 CHECKERS / DECODERS

7.3 Gates • Gates can have more than 2 inputs but the functions stay the same – AND = output = 1 if ALL inputs are 1 • Outputs 1 for only 1 input combination – OR = output = 1 if ANY input is 1 • Outputs 0 for only 1 input combination X Y Z F X Y Z F 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 x 0 1 0 0 0 1 0 1 x F y F y 0 1 1 0 0 1 1 1 z z 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 1 1 1 1 1 3-input AND 3-input OR

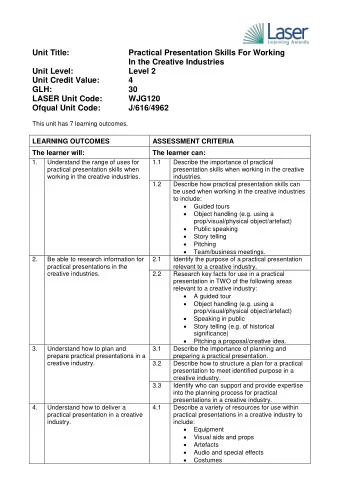
7.4 Checkers / Decoders • An AND gate only outputs ‘1’ for 1 combination – That combination can be changed by adding inverters to the inputs – We can think of the AND gate as “checking” or “decoding” a specific combination and outputting a ‘1’ when it matches. X Y Z F X Y Z F 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 0 x 0 1 0 0 x 0 1 0 0 F F y y 0 1 1 0 0 1 1 0 z z 1 0 0 0 1 0 0 0 1 0 1 1 1 0 1 0 AND gate decoding AND gate decoding 1 1 0 0 1 1 0 0 (checking for) (checking for) combination 000 combination 101 1 1 1 0 1 1 1 0

7.5 Checkers / Decoders • Place inverters at the input of the AND gates such that – F produces ‘1’ only for input combination {x,y,z} = {010} – G produces ‘1’ only for input combination {x,y,z} = {110} X Y Z F X Y Z G 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 x 0 1 0 1 x 0 1 0 0 F G y y 0 1 1 0 0 1 1 0 z z 1 0 0 0 1 0 0 0 1 0 1 0 1 0 1 0 AND gate decoding AND gate decoding 1 1 0 0 1 1 0 1 (checking for) (checking for) combination 110 combination 010 1 1 1 0 1 1 1 0

7.6 Checkers / Decoders • An OR gate only outputs ‘0’ for 1 combination – That combination can be changed by adding inverters to the inputs – We can think of the OR gate as “checking” or “decoding” a specific combination and outputting a ‘0’ when it matches. X Y Z F X Y Z F 0 0 0 1 0 0 0 1 0 0 1 1 0 0 1 1 0 1 0 0 x 0 1 0 1 x F y F y 0 1 1 1 0 1 1 1 z z 1 0 0 1 1 0 0 1 1 0 1 1 1 0 1 1 1 1 0 1 1 1 0 0 OR gate decoding OR gate decoding (checking for) 1 1 1 1 (checking for) 1 1 1 1 combination 010 combination 110

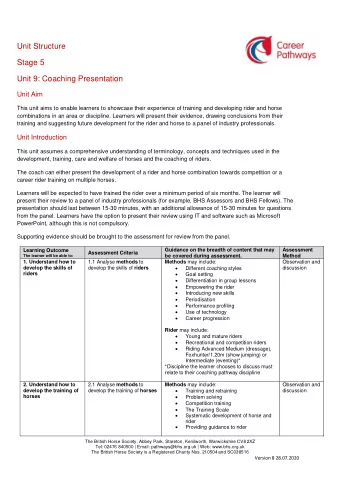
7.7 Decoder Exercise • Compilers translate software to instructions Instruction Type 6-bit OPCODE that tell the processor to ADD, LOAD from OP[5:0] Memory, Store to Memory, etc. ADD 001000 • These instructions are binary codes LOAD 100011 • The processor must decode the instruction STORE 101011 • Create an AND gate decoder for each instruction type in the table that will BRANCH 000100 produce '1' when that instruction is about to be executed STORE LOAD ADD

7.8 Full Decoders • A full decoder is a building block that: – Takes in an n-bit binary number as input – Decodes that binary number and activates the corresponding output – Individual outputs for ALL 2 n input combinations There are gates inside to implement each 3-to-8 Decoder output D0 D1 D2 1 output for each Z (LSB) 3-bit binary D3 combination of the Y number D4 input number X (MSB) D5 D6 D7

7.9 Decoders • A decoder is a building block that: – Takes a binary number as input – Decodes that binary number and activates the corresponding output – Put in 6=110, Output 6 activates (‘1’) – Put in 5=101, Output 5 activates (‘1’) 0 D0 0 D1 0 D2 0 Z (LSB) 0 D3 1 Y 0 D4 1 X (MSB) Only that 0 D5 numbered output is 1 D6 Binary #6 activated 0 D7

7.10 Decoders • A decoder is a building block that: – Takes a binary number as input – Decodes that binary number and activates the corresponding output – Put in 6=110, Output 6 activates (‘1’) – Put in 5=101, Output 5 activates (‘1’) 0 D0 0 D1 0 D2 1 Z (LSB) 0 D3 0 Y Only that 0 D4 1 X (MSB) numbered output is 1 D5 activated 0 D6 Binary #5 0 D7

7.11 Decoder Sizes • A decoder w/ an n-bit input has 2 n outputs – 1 output for every combination of the n-bit input 1 Y0 0 Y1 Y2 0 0 A0 0 D0 0 0 Y Y3 0 0 D1 A1 Y4 0 1 0 D2 (MSB) A2 1 (MSB) X 0 0 D3 Y5 Y6 0 2 n outputs n inputs 0 Y7 (2) (4) 2 n outputs n inputs (3) (8) 2-to-4 3-to-8 Decoder Decoder

7.12 Exercise • Complete the design of a 2-to-4 decoder X Y D0 D1 D2 D3 D0 0 0 1 0 0 0 Y D1 0 1 0 1 0 0 D2 (MSB) X D3 1 0 0 0 1 0 1 1 0 0 0 1 D0 y D1 D2 x D3

7.13 Building Decoders O0 Checker O0 for 000 A0 O1 Checker O1 for 001 O2 Checker O2 for 010 A1 O3 Checker O3 for 011 3-bit O4 Checker O4 number A2 for 100 [A2:A0] O5 Checker O5 for 101 Checker O6 O6 for 110 Checker O7 O7 for 111

7.14 Vending Machine Example Assuming the keypad produces a 4-bit numeric output, add logic to produce the release signals for each of the 16 vending items. 1 2 3 0 1 2 3 4 5 6 7 8 9 4 5 6 7 0 8 9 10 11 A[3:0] 12 13 14 15 4-to-16 decoder 0 1 2 3 … 15 Consider any problems with this design.

7.15 Enables • In a normal decoder exactly one output is active at all times • It may be undesirable to always have an active output • We can add an extra input (called an enable) that can independently force all the outputs to their inactive values 0 D0 D0 1 Y Y One output 1 D1 D1 will always 0 D2 D2 0 (MSB) (MSB) X be active X 0 D3 D3 E 2-to-4 Decoder Enable Will force all outputs to 0 when E = 0 (i.e. not enabled)

7.16 Enables 0 D0 1 Y 0 When E=0, Since E=0, D1 inputs is all outputs = 0 0 D2 0 (MSB) X ignored 0 D3 E 0 Enable 0 D0 When E=1, 1 Y 1 inputs will cause the Since E=1, D1 appropriate output to outputs will 0 D2 0 (MSB) X go active function normally 0 D3 E 1 Enable

7.17 Enables • Enables can be implemented by connecting it to each AND gate of the decoder A ’ B ’ A B D0 A D1 D2 (MSB) B D3 E When E=0, 0 AND anything = 0 When E=1, 1 AND anything = that anything, which was the normal decoding logic

7.18 Multiplexers • Multiplexers are one of the most common digital circuits • Anatomy: n data inputs, log 2 n select bits, 1 output • A multiplexer (“mux” for short) selects one data input and passes it to the output 4-to-1 Mux S 1 S 0 Y 0 0 i0 i0 0 1 i1 i1 y 1 0 i2 n data inputs 1 output i2 1 1 I3 i3 s log 2 n select bits

7.19 Multiplexers 4-to-1 Mux i0 A i1 B y C 2 Thus, input 2 = C is i2 C S 1 S 0 Y selected and passed i3 D to the output 0 0 i0 s 0 1 i1 1 1 0 i2 Select bits = 10 2 = 2 10 . 1 1 I3

7.20 Multiplexers 4-to-1 Mux, 32-bit wide mux i0 A i1 B y A 2 Thus, input 0 = A is i2 C S 1 S 0 Y selected and passed i3 D to the output 0 0 i0 s 0 1 i1 1 1 0 i2 Select bits = 00 2 = 0 10 . 1 1 I3

7.21 Multiplexers 2-to-1 Mux, 32-bit wide mux i0 A y B 2 Thus, input 1 = B is S Y selected and passed i1 B to the output 0 i0 s 1 I1 1 Select bits = 1 2 = 1 10 .

7.22 Recall Using T1/T2 1 st Level of AND gates act as barriers only passing 1 channel • • OR gates combines 3 streams of 0’s with the 1 channel that got passed (i.e. ICH1) 2 nd Level of AND gates passes the channel to only the selected output • Connection Essentially this logic ICH1 ICH 0 Point 0 0 forms a 4-to-1 mux OCH 0 where one level of 0 0 gates blocks all but 1 ICH1 ICH1 and then the OR gate ICH 1 0 combines all signals OCH 1 ICH1 1 0 ICH 2 ICH1 0 0 OCH 2 0 0 ICH 3 ICH1 ICH1 0 OCH 3 0 1 0 1 0 0 0 0 0 1 AND: OR: AND: OSEL0 OSEL1 OSEL2 OSEL3 ISEL0 ISEL1 ISEL2 ISEL3 1 AND ICHx = ICHx 0 + ICH1 + 0 + 0 1 AND ICH1 = ICH1 0 AND ICHx = 0 = ICH1 0 AND ICH1 = 0

7.23 Exercise: Build a 4-to-1 mux I 0 • Complete the 4-to-1 I 1 mux to the right by Y I 2 drawing wires between the 2-to-4 I 3 decode and the AND S 1 S 0 =00 gates AND Gates acting as barrier gates S 1 S 0 =01 S 1 S 0 =10 Final OR gate takes 3 zero s and one selected input S 1 S 0 =11 2-to-4 Decoder S 1 S 0

7.24 Building a Mux • To build a mux – Decode the select bits and include the corresponding data input. – Finally OR all the first level outputs together. S 1 S 0 Y 0 I 0 0 0 i0 1 S 0 S 1 0 1 i1 0 1 0 i2 I 1 I 1 I 1 1 1 i3 S 0 1 1 S 1 S 1 S 0 = 01 2 1 0 I 1 Y 0 I 2 S 0 1 S 1 0 0 I 3 S 0 1 S 1 0

7.25 Building a Mux • To build a mux – Decode the select bits and include the corresponding data input. – Finally OR all the first level outputs together. S 1 S 0 Y 0 I 0 0 0 i0 1 S 0 S 1 0 1 i1 1 1 0 i2 0 I 1 1 1 i3 S 0 1 S 1 S 1 S 0 = 11 2 1 I 3 Y 0 I 2 S 0 1 S 1 1 I 3 I 3 I 3 S 0 1 1 S 1 1 1

7.26 Building a Mux • To build a mux – Decode the select bits and include the corresponding data input. – Finally OR all the first level outputs together. 0 1 1 0 I1 I0 1 0 1 0