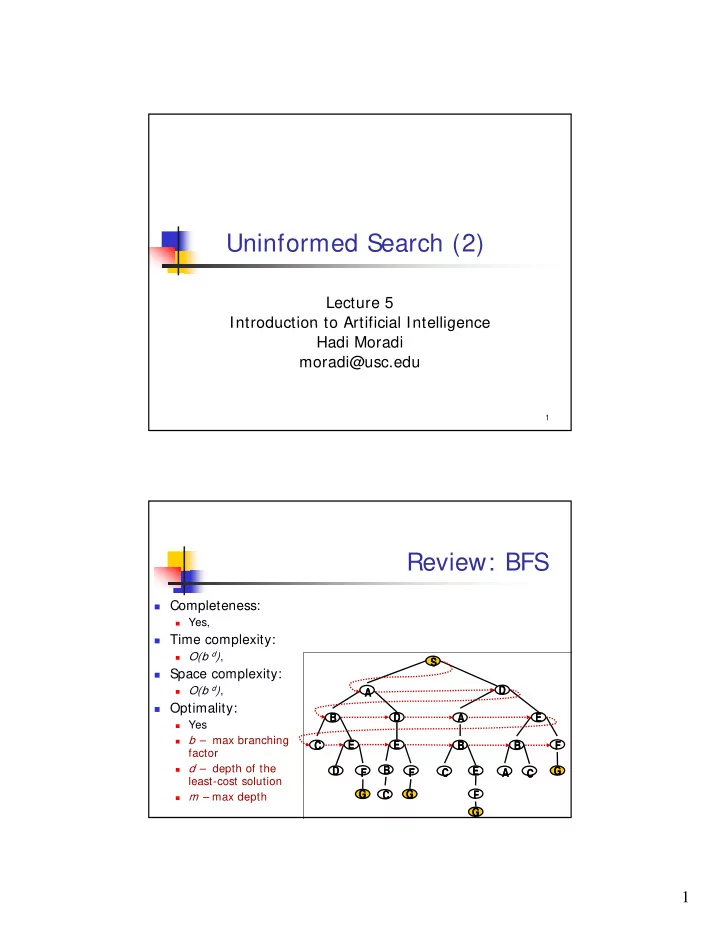
Uninformed Search (2) Lecture 5 Introduction to Artificial - PDF document

Uninformed Search (2) Lecture 5 Introduction to Artificial Intelligence Introduction to Artificial Intelligence Hadi Moradi moradi@usc.edu 1 Review: BFS � Completeness: � Completeness: � Yes, � Time complexity: � O(b d ) , S � Space complexity: � O(b d ) , D A � Optimality: Optimality: D E E B A � Yes � b – max branching C E E B B F factor � d – depth of the B D E G F F C A C least-cost solution G C G F � m – max depth 2 G 1

Review: Uniform Cost � Completeness: S S 3 4 � Yes, 4 3 � Time complexity: D 5 4 A 5 2 � O(b d ) , 6 7 9 8 � Space complexity: B A D E E 5 4 5 4 5 4 � O(b d ) , 11 11 10 10 11 11 12 12 13 13 13 13 C B B F E E � Optimality: � Optimality: 3 � Yes 13 13 B D E G F F C A C C F G G G 3 Review: DFS � Completeness: � Completeness: Yes Yes, � Time complexity: O(b m ) , S S � Space complexity: O(bm) , � Optimality: No A � b – max branching factor � d – depth of the least-cost B solution solution � m – max depth C E D F G 4 2

Depth First Search � Problem: Not remembering the previous � Problem: Not remembering the previous states � Time complexity � Solution: � Combine the depth first search and breath first p search 5 Depth-limited search It i It is a depth-first search with depth limit d th fi t h ith d th li it I mplementation: Nodes at depth l have no successors. Complete : Optimal: p 6 3

Iterative deepening search Function Iterative-deepening-Search( problem ) returns a solution, or failure p g ( p ) , for depth = 0 to ∞ do result � Depth-Limited-Search( problem , depth ) if result succeeds then return result end return failure Combines the best of breadth-first and depth-first search strategies. • Completeness: • Time complexity: • Space complexity: • Optimality: 7 Romania with step costs in km 8 4

9 10 5

11 12 6

13 14 7

15 16 8

Iterative deepening complexity � Iterative deepening search may seem wasteful � Iterative deepening search may seem wasteful because so many states are expanded multiple times. 17 Bidirectional search � Both search forward from initial state, Both search forward from initial state and backwards from goal. � Stop when the two searches meet in the middle. Start Start Goal Goal 18 9

Bidirectional search 1 QUEUE1 < 1 QUEUE1 < 1. QUEUE1 < 1. QUEUE1 < -- -- path only containing the root; path only containing the root; path only containing the root; path only containing the root; QUEUE2 < QUEUE2 < -- -- path only containing the goal; path only containing the goal; 2. WHILE 2. WHILE both QUEUEs are not empty both QUEUEs are not empty AND AND QUEUE1 and QUEUE2 do NOT share a state QUEUE1 and QUEUE2 do NOT share a state DO DO remove their first paths; remove their first paths; create their new paths (to all children); create their new paths (to all children); p p ( ( ); ); reject their new paths with loops; reject their new paths with loops; add their new paths to back; add their new paths to back; 3. 3. IF IF QUEUE1 and QUEUE2 share a state QUEUE1 and QUEUE2 share a state THEN THEN success; success; ELSE failure; ELSE failure; 19 Bidirectional search • • Completeness: Completeness: • Time complexity: • Space complexity: • Optimality: 20 10

Bidirectional search � Bidirectional search merits Bidirectional search merits � Big difference for problems with branching factor b in both directions 21 Bidirectional search � Bidirectional search issues � Predecessors of a node need to be generated � What to do if there is no explicit list of goal states? � What is the best search strategy for the two searches? 22 11

Comparing uninformed search strategies Criterion Breadth Uniform DepthFirst DepthLim Iterative Bidirectional Time b^ d b^ d b^ m b^ l b^ d b^ (d/2) Space b^ d b^ d bm bl bd b^ (d/2) Optimal? Yes Yes No No Yes Yes Complete? Yes Yes No Yes if l ≥ d Yes Yes � b – max branching factor of the search tree � d – depth of the least-cost solution � m – max depth of the state-space (may be infinity) 23 � l – depth cutoff Summary � Problem formulation usually requires Problem formulation usually requires abstracting away real-world details to define a state space that can be explored using computer algorithms. � Once problem is formulated in abstract form, complexity analysis helps us picking out best algorithm to solve problem. 24 12

Summary � Variety of uninformed search strategies; Variety of uninformed search strategies; difference lies in method used to pick node that will be further expanded. � Iterative deepening search only uses � Iterative deepening search only uses linear space and not much more time than other uniformed search strategies. 25 13