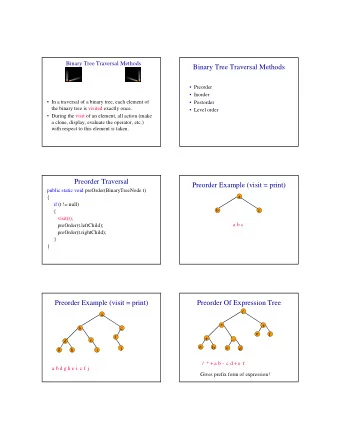
Traversal time for weakly synchronized CAN bus Hugo Daigmorte, Marc - PowerPoint PPT Presentation
Context and goal Computing an upper bound on network delay Experimental results Conclusion Traversal time for weakly synchronized CAN bus Hugo Daigmorte, Marc Boyer ONERA The French aerospace lab 24th International Conference on Real-Time
Context and goal Computing an upper bound on network delay Experimental results Conclusion Traversal time for weakly synchronized CAN bus Hugo Daigmorte, Marc Boyer ONERA – The French aerospace lab 24th International Conference on Real-Time Networks and Systems RTNS’2016 19th October 2016 A r t i * f a S * C o m p l N e t n e t e t * c T i s W n s R o e l t C l * d * e c o * s u d e u m E r e n e o t y d e t v s a E * t a a u l H. Daigmorte, M. Boyer Traversal time for weakly synchronized CAN bus 1 / 24
Context and goal Context and goal Computing an upper bound on network delay Global clock Experimental results Local clock Conclusion Bounded phases Table of Contents Context and goal 1 Context and goal Global clock Local clock Bounded phases Computing an upper bound on network delay 2 Experimental results 3 Conclusion 4 H. Daigmorte, M. Boyer Traversal time for weakly synchronized CAN bus 2 / 24
Context and goal Context and goal Computing an upper bound on network delay Global clock Experimental results Local clock Conclusion Bounded phases Context Context Real-time networked system Bus network: CAN Periodic flows with Offsets reduces contentions ⇒ reduces delays requires synchronization CAN Node CAN Node CAN Node n°1 n°2 n°N H. Daigmorte, M. Boyer Traversal time for weakly synchronized CAN bus 3 / 24
Context and goal Context and goal Computing an upper bound on network delay Global clock Experimental results Local clock Conclusion Bounded phases Model and Goal Model Flows F i : P i , S i , O i N nodes, each node j has a clock: c j ( t ) Sending frame k: c j ( t ) = O i + kP i Goal Accurate bound on network traversal time aka Worst Case Traversal Time (WCTT) H. Daigmorte, M. Boyer Traversal time for weakly synchronized CAN bus 4 / 24
Context and goal Context and goal Computing an upper bound on network delay Global clock Experimental results Local clock Conclusion Bounded phases Global clock ∀ j , j ′ : c j ( t ) = c j ′ ( t ) Advantage: efficient schedule ⇒ no contention Drawback: perfect synchronization (HW/SW cost) N1 A,1 B,1 A,2 N2 C,1 C,2 C,3 BUS BUS A,1 C,1 B,1 C,2 A,2 C,3 H. Daigmorte, M. Boyer Traversal time for weakly synchronized CAN bus 5 / 24
Context and goal Context and goal Computing an upper bound on network delay Global clock Experimental results Local clock Conclusion Bounded phases Local clock Advantage: efficient schedule ⇒ no contention intra-nodes efficient schedule ⇒ workload spread over time A,1 B,1 A,2 N1 C,1 C,2 C,3 N2 A,1 C,1 B,1 C,2 A,2 C,3 BUS BUS H. Daigmorte, M. Boyer Traversal time for weakly synchronized CAN bus 6 / 24
Context and goal Context and goal Computing an upper bound on network delay Global clock Experimental results Local clock Conclusion Bounded phases Bounded phases ∀ j , j ′ : c j ( t ) − c j ′ ( t ) ≤ Φ j , j ′ Objectives: affordable synchronization reduces delays wrt no sync/local clock A,1 B,1 A,2 N1 C,1 C,2 C,3 N2 A,1 C,1 B,1 C,2 A,2 C,3 BUS BUS H. Daigmorte, M. Boyer Traversal time for weakly synchronized CAN bus 7 / 24
Context and goal Computing an upper bound on network delay Network Calculus Experimental results Methodology Conclusion Table of Contents Context and goal 1 Computing an upper bound on network delay 2 Network Calculus Methodology Experimental results 3 Conclusion 4 H. Daigmorte, M. Boyer Traversal time for weakly synchronized CAN bus 8 / 24
Context and goal Computing an upper bound on network delay Network Calculus Experimental results Methodology Conclusion Reality modeling Network Calculus is a theory designed to compute memory and delay bounds in networks. A α A + A ′ Flow : Cumulative curve A A(t) : amount of data sent up to time t Properties: null at 0 (and before), non decreasing Server: simple arrival/departure relation: Property: departure produced after arrival: S A − → D = ⇒ A ≥ D Worst delay: t ∈ R + { inf { d ∈ R + | A ( t ) ≤ D ( t + d ) }} d ( A , S ) = sup H. Daigmorte, M. Boyer Traversal time for weakly synchronized CAN bus 9 / 24
Context and goal Computing an upper bound on network delay Network Calculus Experimental results Methodology Conclusion Arrival curve and services Real behaviors are unknown at design time ⇒ use of contracts Traffic contract: arrival curve A flow A has arrival curve α iff: ∀ t , d ∈ R + : A ( t + d ) − A ( t ) ≤ α ( d ) Server contract: service curve For t , s in the same busy/backlogged period, a server S offers a strict minimal service of curve β iff: D ( t ) − D ( s ) ≥ β ( t − s ) H. Daigmorte, M. Boyer Traversal time for weakly synchronized CAN bus 10 / 24
Context and goal Computing an upper bound on network delay Network Calculus Experimental results Methodology Conclusion A common period Problem transformation H. Daigmorte, M. Boyer Traversal time for weakly synchronized CAN bus 11 / 24
Context and goal Computing an upper bound on network delay Network Calculus Experimental results Methodology Conclusion A common period Problem transformation Initial problem: Flow : F i = < T i , O i , S i >, F = { F 1 , .., F n } 1 source periodic messages Size, Period, Offset Priority H. Daigmorte, M. Boyer Traversal time for weakly synchronized CAN bus 11 / 24
Context and goal Computing an upper bound on network delay Network Calculus Experimental results Methodology Conclusion A common period Problem transformation Initial problem: Flow : F i = < T i , O i , S i >, F = { F 1 , .., F n } 1 source periodic messages Size, Period, Offset Priority Transformed problem: A = { A 1 , .., A m } Period T = ppcm ( T i ) Offset O j Size S j Donner un exemple (avec figure) H. Daigmorte, M. Boyer Traversal time for weakly synchronized CAN bus 11 / 24
Context and goal Computing an upper bound on network delay Network Calculus Experimental results Methodology Conclusion Arrival curve Arrival curve α 1 .. k (Theorem 5) Capture the synchronization Efficient algorithm Required common period H. Daigmorte, M. Boyer Traversal time for weakly synchronized CAN bus 12 / 24
Context and goal Computing an upper bound on network delay Network Calculus Experimental results Methodology Conclusion α P O A α P A ′ O ′ 2 α α A + A ′ A + A ′ H. Daigmorte, M. Boyer Traversal time for weakly synchronized CAN bus 13 / 24
Context and goal Computing an upper bound on network delay Network Calculus Experimental results Methodology Conclusion State of the art: hDev ( A i , D i ) ≤ hDev ( α i , β − � α j − L ) j < i 1 Method 1: hDev ( A i , D i ) ≤ hDev ( α i , β − α 1 .. i − 1 − L ) Taking into account synchronization between flows A 1 .. A i − 1 α i β − α 1 .. i − 1 − L hDev ( α i , β i − α 1 .. i − 1 ) H. Daigmorte, M. Boyer Traversal time for weakly synchronized CAN bus 14 / 24
Context and goal Computing an upper bound on network delay Network Calculus Experimental results Methodology Conclusion 2 Method 2: hDev ( A i , D i ) ≤ ( β − α 1 .. i − L ) − 1 (0) Bound busy period for high priority flows (1..i) Pessimistic if several messages of the same flow are in the same busy period i,1 i,2 i,1 i,2 8,6cm β α 1 - 1 ( - - L ) ( 0 ) . . i H. Daigmorte, M. Boyer Traversal time for weakly synchronized CAN bus 15 / 24
Context and goal Computing an upper bound on network delay Network Calculus Experimental results Methodology Conclusion 3 Method 3 (Theorem 3): hDev ( A i , D i ) ≤ hDev ( A i , D i ) Requires good knowledge of A i hDev ( A i , D i ) A i D i D i hDev ( A i , D i ) H. Daigmorte, M. Boyer Traversal time for weakly synchronized CAN bus 16 / 24
Context and goal Phases bounded by 0ms Computing an upper bound on network delay Phases bounded by ± 1ms Experimental results Phases bounded by ± 5ms Conclusion Phases bounded by ± 10ms Table of Contents Context and goal 1 Computing an upper bound on network delay 2 Experimental results 3 Phases bounded by 0ms Phases bounded by ± 1ms Phases bounded by ± 5ms Phases bounded by ± 10ms Conclusion 4 H. Daigmorte, M. Boyer Traversal time for weakly synchronized CAN bus 17 / 24
Context and goal Phases bounded by 0ms Computing an upper bound on network delay Phases bounded by ± 1ms Experimental results Phases bounded by ± 5ms Conclusion Phases bounded by ± 10ms Configuration under study 250 kbit/s 2 2 1 3 4 3 1 10 3 1 3 1 1 1 10 nodes Period (ms) 1 2 1 3 1 2 3 62 flows 10 2 1 2 1 1 2 1 3 1 3 1 Load: 35% 1 1 2 1 2 2 1 Period: { 20,50,100,200,500,1000 } 10 1 0 1 2 3 4 5 6 7 8 9 Frame payload (bytes) Payload: 1-8 bytes Method Synchronization WCTT Method 1 Phases Bound Method 2 Phases Bound Phases Bound Method 3 Local clocks Exact Method 4 Method 5 Global clock Bound Method 6 No offsets Exact Phases : c j ( t ) − c ′ j ( t ) ≤ Φ, Local clocks : Φ = ∞ , Global clocks : Φ = 0, No offset : O i = 0 / unknown H. Daigmorte, M. Boyer Traversal time for weakly synchronized CAN bus 18 / 24
Recommend
More recommend
Explore More Topics
Stay informed with curated content and fresh updates.