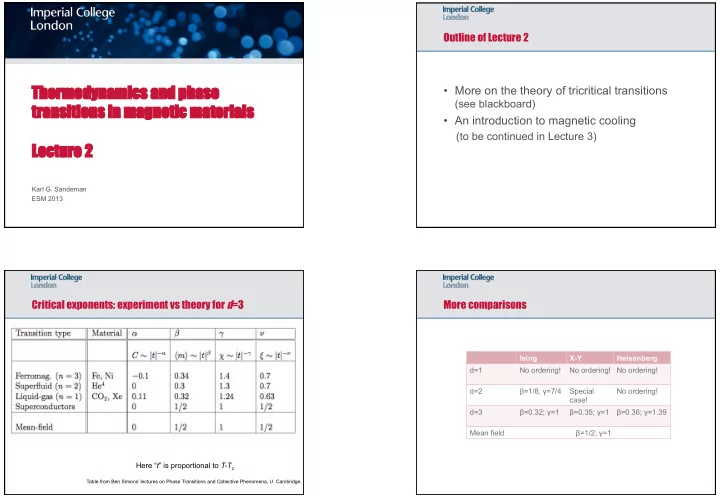

Outline of Lecture 2 Thermo modynami mics and ph phase • More on the theory of tricritical transitions (see blackboard) transitions in ma magnetic ma materials • An introduction to magnetic cooling (to be continued in Lecture 3) Lec Lectur ure 2 e 2 Karl G. Sandeman ESM 2013 Critical exponents: experiment vs theory for d =3 More comparisons Ising X-Y Heisenberg d=1 No ordering! No ordering! No ordering! d=2 β =1/8; γ =7/4 Special No ordering! case! d=3 β =0.32; γ =1 β =0.35; γ =1 β =0.36; γ =1.39 Mean field β =1/2; γ =1 Here “ t ” is proportional to T-T c Table from Ben Simons’ lectures on Phase Transitions and Collective Phenomena, U. Cambridge.
A phase diagram of the Ginzburg-Landau Hamiltonian CoMnSi: imaging tricriticality using a Hall probe CoMnSi 0.92 Ge 0.08 Antiferromagnet to high-magnetisation state, induced by field Low T: - 1st order - Globally “continuous” - Locally sharp, hysteretic High T: - 2nd order - Globally and locally continuous - No hysteresis This diagram is from Ben Simons’ lectures on Phase Transitions and Collective Phenomena, U. Cambridge. Morrison et al., Phys. Rev. B (2009) Vapour compression refrigeration Solid-state cooling at room temperature Refrigerant Critical Critical temp. pressure CO 2 31 ˚C 7.38 MPa Ferroic cooling, R22 96.2 ˚C 4.99 MPa R134a 101 ˚C 4.06 MPa including magnetic cooling The efficiency of the refrigerant is directly related to the critical Gas compression refrigeration temperature. works in sub-critical regime Tuning the critical point and the pressure-temperature phase line gradient are very important
Magnetic refrigeration: a growing area of interest Magnetic cooling: the future m = l ∑ ∑ m ( H M ) d ( Y l m ( Ω M )) dG = − SdT − MdH M + K l + Vdp + ... A careful system-wide cost and efficiency analysis revealed the benefit of l m = − l magnetic cooling at low powers (< 500 Watt). A research frontier Magnetocaloric principles Can also be described in terms of isothermal entropy change , Δ S: Energy efficiency Rare earth Apply magnetic field metal use H $ ' ∂ M ( T ', H ') adiabatically ∫ Δ S total ( H , T ) = dH ' & ) % ∂ T ' ( 0 H ' S total =S magnetic + S lattice + S electronic Maxwell relation for continuous M(T,H) Magnetic cooling S magnetic high S magnetic low S lattice low S lattice high Δ S total ( H , T ) = −Δ M dH c dT Δ T ad ( H , T ) = T Δ S Clausius-Clapeyron eqn. for 1st order C p transition in M Magnetic phase HFC-free cooling transition physics So the material (usually) heats in an applied field ( Δ T ad >0) The effect is maximal at a (magnetic) phase transition The sign of (dM/dT) is crucial and yields two possibilities for the MCE
Magnetocaloric benchmark material at RT: Gd The cycle K-type thermocouple A d i a b a t i c M a g n e t o c a l o r i c E f f e c t i n G d ( 0 - 2 T ) 5 Temperature Change (˚C) Gd 4 3 2 1 magnetic field 0 - 2 0 - 1 0 0 1 0 2 0 3 0 4 0 T e m p e r a t u r e ( D e g r e e s C ) K. G. Sandeman, Mag. Tech. Int. 1 30-32 (2011) � Magnetocaloric principles State of the art (2010) Inverse Inverse M M Lists 41 prototypes to 2010. Most used Gd as refrigerant at that time. No clear example of end-user integration at that time. The situation has already changed in the 3 years since… T c T T t T c T
What makes a good magnetic refrigerant? Single phase refrigerants A candidate magnetic refrigerant at room temperature: La(Fe,Si) 13 Cheap MnFe(P,Z) d-metal magnetism La(Fe,Co,Mn,Si) 13 ~11.6 Å First order transition Δ T ad ( H , T ) = T Δ S because ∆ T ad of second order transtion is too low (if d-metal C p alloy) 2 nd H Proximity to (tri)critical point order Minimise energy loss from hysteresis 1 st order ∂ H of phase line is also important (see next) T C ∂ T T La(Fe,Si) 13 cubic crystal structure Fujita et al., 2003 Tuning transition temperature La-Fe-Co-Si La-Fe-Mn-Si-H 14,0 x = 0.050 y=0.390 x = 0.058 y=0.373 10,00 y=0.356 x = 0.065 12,0 y=0.338 x = 0.075 y=0.322 8,00 x = 0.087 10,0 x = 0.099 - Δ S m (Jkg -1 K -1 ) - Δ S m (J/kgK) x = 0.112 8,0 6,00 Gd 6,0 4,00 4,0 2,00 2,0 0,00 0,0 -30,0 -20,0 -10,0 0,0 10,0 20,0 30,0 40,0 50,0 60,0 70,0 80,0 270 280 290 300 310 T (°C) Temperature (K) Magnetic entropy change as a function of temperature of: La(Fe 0.915 Co x Si 0.085 ) 13 ( left ) and five LaFe 11.74-y Mn y Si 1.26 H 1.53 alloys with different y ( right ) for a magnetic field change of 1.6 T. The entropy change is higher than that seen in gadolinium (Gd, left plot only).
Recommend
More recommend