The Toda lattice and Bruhat interval polytopes Lauren K. Williams, - PowerPoint PPT Presentation

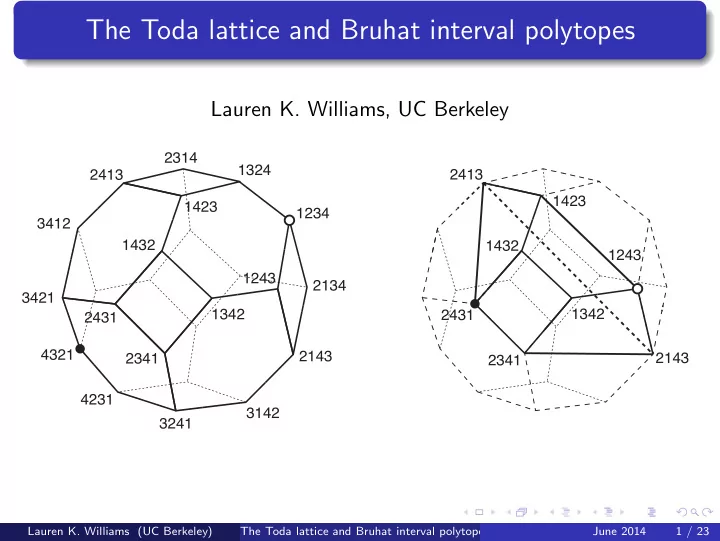
The Toda lattice and Bruhat interval polytopes Lauren K. Williams, UC Berkeley 2314 1324 2413 2413 1423 1423 1234 3412 1432 1432 1243 1243 2134 3421 1342 2431 1342 2431 4321 2143 2341 2143 2341 4231 3142 3241 Lauren K. Williams (UC Berkeley) The Toda lattice and Bruhat interval polytopes June 2014 1 / 23

Plan of the talk Introduction to the Toda lattice The sorting property The positive flag variety, and generalized sorting. Bruhat interval polytopes and their faces The generalized lifting property and R -polynomials Combinatorics of Bruhat interval polytopes Bruhat interval polytopes for G / P References (joint with Yuji Kodama) The full Kostant-Toda hierarchy on the positive flag variety, to appear in Comm. Math. Phys. (joint with Emmanuel Tsukerman) Bruhat Interval Polytopes, arXiv:1406.5202 Lauren K. Williams (UC Berkeley) The Toda lattice and Bruhat interval polytopes June 2014 2 / 23

The Toda lattice The Toda lattice is defined by dL dt = [ π ( L ) , L ] , where L = L ( t ) is a tridiagonal symmetric matrix and π ( L ) is its skew-symmetric projection:     b 1 a 1 0 · · · 0 0 a 1 0 · · · 0 a 1 b 2 a 2 · · · 0 − a 1 0 a 2 · · · 0         0 · · · 0 0 − a 2 0 · · · 0 a 2 b 3 L = , π ( L ) = .      . .   . .  ... ... ... ... ... ... . . . .     . . . .     0 · · · · · · a n − 1 b n 0 · · · · · · − a n − 1 0 Model introduced by Toda in 1967 (Def above due to Flaschka 1974) Represents dynamics of n particles of unit mass, moving on a line under influence of exponential repulsive forces. Eigenvalues of L ( t ) are independent of t . Lauren K. Williams (UC Berkeley) The Toda lattice and Bruhat interval polytopes June 2014 3 / 23

The Toda lattice The Toda lattice is defined by dL dt = [ π ( L ) , L ] , where L = L ( t ) is a tridiagonal symmetric matrix and π ( L ) is its skew-symmetric projection:     b 1 a 1 0 · · · 0 0 a 1 0 · · · 0 a 1 b 2 a 2 · · · 0 − a 1 0 a 2 · · · 0         0 · · · 0 0 − a 2 0 · · · 0 a 2 b 3 L = , π ( L ) = .      . .   . .  ... ... ... ... ... ... . . . .     . . . .     0 · · · · · · a n − 1 b n 0 · · · · · · − a n − 1 0 Model introduced by Toda in 1967 (Def above due to Flaschka 1974) Represents dynamics of n particles of unit mass, moving on a line under influence of exponential repulsive forces. Eigenvalues of L ( t ) are independent of t . Lauren K. Williams (UC Berkeley) The Toda lattice and Bruhat interval polytopes June 2014 3 / 23

The Toda lattice The Toda lattice is defined by dL dt = [ π ( L ) , L ] , where L = L ( t ) is a tridiagonal symmetric matrix and π ( L ) is its skew-symmetric projection:     b 1 a 1 0 · · · 0 0 a 1 0 · · · 0 a 1 b 2 a 2 · · · 0 − a 1 0 a 2 · · · 0         0 · · · 0 0 − a 2 0 · · · 0 a 2 b 3 L = , π ( L ) = .      . .   . .  ... ... ... ... ... ... . . . .     . . . .     0 · · · · · · a n − 1 b n 0 · · · · · · − a n − 1 0 Model introduced by Toda in 1967 (Def above due to Flaschka 1974) Represents dynamics of n particles of unit mass, moving on a line under influence of exponential repulsive forces. Eigenvalues of L ( t ) are independent of t . Lauren K. Williams (UC Berkeley) The Toda lattice and Bruhat interval polytopes June 2014 3 / 23

The Toda lattice The Toda lattice is defined by dL dt = [ π ( L ) , L ] , where L = L ( t ) is a tridiagonal symmetric matrix and π ( L ) is its skew-symmetric projection:     b 1 a 1 0 · · · 0 0 a 1 0 · · · 0 a 1 b 2 a 2 · · · 0 − a 1 0 a 2 · · · 0         0 · · · 0 0 − a 2 0 · · · 0 a 2 b 3 L = , π ( L ) = .      . .   . .  ... ... ... ... ... ... . . . .     . . . .     0 · · · · · · a n − 1 b n 0 · · · · · · − a n − 1 0 Model introduced by Toda in 1967 (Def above due to Flaschka 1974) Represents dynamics of n particles of unit mass, moving on a line under influence of exponential repulsive forces. Eigenvalues of L ( t ) are independent of t . Lauren K. Williams (UC Berkeley) The Toda lattice and Bruhat interval polytopes June 2014 3 / 23

The Toda lattice The Toda lattice is defined by dL dt = [ π ( L ) , L ] , where L = L ( t ) is a tridiagonal symmetric matrix and π ( L ) is its skew-symmetric projection:     b 1 a 1 0 · · · 0 0 a 1 0 · · · 0 a 1 b 2 a 2 · · · 0 − a 1 0 a 2 · · · 0         0 · · · 0 0 − a 2 0 · · · 0 a 2 b 3 L = , π ( L ) = .      . .   . .  ... ... ... ... ... ... . . . .     . . . .     0 · · · · · · a n − 1 b n 0 · · · · · · − a n − 1 0 Model introduced by Toda in 1967 (Def above due to Flaschka 1974) Represents dynamics of n particles of unit mass, moving on a line under influence of exponential repulsive forces. Eigenvalues of L ( t ) are independent of t . Lauren K. Williams (UC Berkeley) The Toda lattice and Bruhat interval polytopes June 2014 3 / 23

Sorting property of the Toda lattice Suppose the initial matrix L (0) is generic: it has distinct eigenvalues λ 1 < λ 2 < · · · < λ n and a k (0) � = 0 for all k . Then the time evolution of the Toda lattice sorts the eigenvalues of L !   λ 1 0 · · · 0 0 λ 2 · · · 0   t →−∞ L ( t ) = lim  . . .  ... . . .   . . .   0 0 · · · λ n   λ n 0 · · · 0 0 λ n − 1 · · · 0   t → + ∞ L ( t ) = lim  . . .  ... . . .   . . .   0 0 · · · λ 1 Lauren K. Williams (UC Berkeley) The Toda lattice and Bruhat interval polytopes June 2014 4 / 23

Sorting property of the Toda lattice Suppose the initial matrix L (0) is generic: it has distinct eigenvalues λ 1 < λ 2 < · · · < λ n and a k (0) � = 0 for all k . Then the time evolution of the Toda lattice sorts the eigenvalues of L !   λ 1 0 · · · 0 0 λ 2 · · · 0   t →−∞ L ( t ) = lim  . . .  ... . . .   . . .   0 0 · · · λ n   λ n 0 · · · 0 0 λ n − 1 · · · 0   t → + ∞ L ( t ) = lim  . . .  ... . . .   . . .   0 0 · · · λ 1 Lauren K. Williams (UC Berkeley) The Toda lattice and Bruhat interval polytopes June 2014 4 / 23

Sorting property of the Toda lattice Suppose the initial matrix L (0) is generic: it has distinct eigenvalues λ 1 < λ 2 < · · · < λ n and a k (0) � = 0 for all k . Then the time evolution of the Toda lattice sorts the eigenvalues of L !   λ 1 0 · · · 0 0 λ 2 · · · 0   t →−∞ L ( t ) = lim  . . .  ... . . .   . . .   0 0 · · · λ n   λ n 0 · · · 0 0 λ n − 1 · · · 0   t → + ∞ L ( t ) = lim  . . .  ... . . .   . . .   0 0 · · · λ 1 Lauren K. Williams (UC Berkeley) The Toda lattice and Bruhat interval polytopes June 2014 4 / 23

The full symmetric Toda lattice The full symmetric Toda lattice is defined as before by dL dt = [ π ( L ) , L ] , but now L = L ( t ) is any symmetric matrix. Eigenvalues of L ( t ) are independent of t . In generic case, the sorting property holds (Kodama-McLaughlin ’96). In non-generic case, what can we say about lim t →±∞ L ( t )? Lauren K. Williams (UC Berkeley) The Toda lattice and Bruhat interval polytopes June 2014 5 / 23

The full symmetric Toda lattice The full symmetric Toda lattice is defined as before by dL dt = [ π ( L ) , L ] , but now L = L ( t ) is any symmetric matrix. Eigenvalues of L ( t ) are independent of t . In generic case, the sorting property holds (Kodama-McLaughlin ’96). In non-generic case, what can we say about lim t →±∞ L ( t )? Lauren K. Williams (UC Berkeley) The Toda lattice and Bruhat interval polytopes June 2014 5 / 23

The full symmetric Toda lattice The full symmetric Toda lattice is defined as before by dL dt = [ π ( L ) , L ] , but now L = L ( t ) is any symmetric matrix. Eigenvalues of L ( t ) are independent of t . In generic case, the sorting property holds (Kodama-McLaughlin ’96). In non-generic case, what can we say about lim t →±∞ L ( t )? Lauren K. Williams (UC Berkeley) The Toda lattice and Bruhat interval polytopes June 2014 5 / 23

The full symmetric Toda lattice The full symmetric Toda lattice is defined as before by dL dt = [ π ( L ) , L ] , but now L = L ( t ) is any symmetric matrix. Eigenvalues of L ( t ) are independent of t . In generic case, the sorting property holds (Kodama-McLaughlin ’96). In non-generic case, what can we say about lim t →±∞ L ( t )? Lauren K. Williams (UC Berkeley) The Toda lattice and Bruhat interval polytopes June 2014 5 / 23