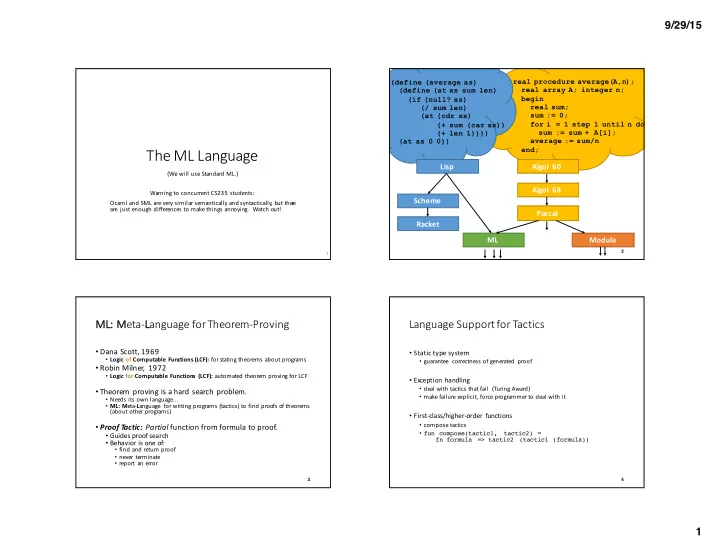

9/29/15 real procedure average(A,n); (define (average as) real array A; integer n; (define (at xs sum len) begin (if (null? xs) real sum; (/ sum len) sum := 0; (at (cdr xs) for i = 1 step 1 until n do (+ sum (car xs)) sum := sum + A[i]; (+ len 1)))) average := sum/n (at as 0 0)) The ¡ML ¡Language end; Lisp Algol ¡ 60 (We ¡will ¡use ¡Standard ¡ML.) Algol ¡ 68 Warning ¡to ¡concurrent ¡CS235 ¡students: Scheme Ocaml and ¡SML ¡are ¡very ¡similar ¡semantically ¡and ¡syntactically , ¡but ¡the r e ¡ are ¡ just ¡enough ¡differences ¡to ¡make ¡things ¡annoying. ¡ ¡Watch ¡out! Pascal Racket ML Modula 2 1 ML ML: ¡ ¡Meta-‑Language ¡for ¡Theorem-‑Proving Language ¡Support ¡for ¡Tactics • Dana ¡Scott, ¡1969 • Static ¡type ¡system ¡ • Logic ¡of Computable ¡Functions ¡(LCF): for ¡stating ¡theorems ¡about ¡programs • guarantee ¡ correctness ¡of ¡generated ¡ proof • Robin ¡Milner, ¡ 1972 • Logic ¡for ¡Computable ¡Functions ¡ ¡(LCF): automated ¡theorem ¡proving ¡for ¡LCF • Exception ¡handling • deal ¡with ¡tactics ¡that ¡fail ¡ ¡(Turing ¡Award) • Theorem ¡ proving ¡is ¡a ¡hard ¡search ¡problem. • make ¡failure ¡explicit, ¡force ¡programmer ¡to ¡deal ¡with ¡it • Needs ¡its ¡own ¡language... • ML: ¡M eta-‑ L anguage ¡ for ¡writing ¡programs ¡(tactics) ¡to ¡find ¡proofs ¡of ¡theorems ¡ (about ¡other ¡programs) • First-‑class/higher-‑order ¡functions • compose ¡tactics • Proof ¡T actic: ¡ Partial ¡ function ¡from ¡formula ¡to ¡proof. • fun compose(tactic1, tactic2) = • Guides ¡proof ¡search fn formula => tactic2 (tactic1 (formula)) • Behavior ¡is ¡one ¡of: • find ¡and ¡return ¡proof • never ¡ terminate • report ¡ an ¡error 3 4 1
9/29/15 The ¡ML ¡language: statically-‑typed, ¡expression-‑oriented Several ¡important ¡ideas ¡beyond ¡what ¡we ¡studied ¡in ¡Racket Static ¡typing Type ¡inference Wipe ¡your ¡syntax ¡slate ¡clean. Algebraic ¡data ¡types Pattern ¡matching Exceptions Modules Much ¡(but ¡not ¡all!) ¡of ¡ML's ¡semantics We ¡will ¡also ¡consider... will ¡seem ¡familiar ¡from ¡Racket. Limited ¡mutation Lazy ¡evaluation Implementation ¡issues ¡for exceptions closures ¡and ¡lexical ¡scope ... ¡And ¡other ¡things ¡along ¡the ¡way... 5 Slides ¡mix ¡material ¡ from ¡Ben, ¡ Steve ¡ Freund, ¡Dan ¡Grossman 6 An ¡ML ¡program ¡is ¡a ¡sequence ¡of ¡bindings. Variable ¡binding (* My first ML program *) val z = (x + y) + (y + 2); (* comment *) val x = 34; val x = e ; More ¡generally: Semicolon ¡optional; may ¡improve ¡debugging. val y = 17; 3 ¡Questions: val z = (x + y) + (y + 2); Syntax : • Keyword val and ¡ punctuation = val q = z + 1; • Variable x • Expression e val abs_of_z = if z < 0 then 0 – z else z; Type-‑checking: • Type-‑check ¡ e : t in ¡the ¡current ¡static ¡environment, ¡for ¡some ¡type ¡ t. val abs_of_z_simpler = abs z • Extend ¡the ¡current ¡static ¡environment ¡with ¡the ¡typing ¡ x : t Evaluation (only ¡for ¡things ¡that ¡type-‑check): (* comment: ML has (* nested comments! *) *) • Evaluate ¡ e to ¡a ¡value ¡ v using ¡the ¡current ¡dynamic ¡environment. • Extend ¡the ¡current ¡dynamic ¡environment ¡with ¡the ¡binding ¡ x à e . 7 8 2
9/29/15 Bindings, ¡types, ¡and ¡environments Expressions ¡and ¡types • A ¡program ¡is ¡a ¡sequence ¡of ¡ bindings. • e : t means ¡"expression ¡ e has ¡type ¡ t " • Bindings ¡build ¡ two environments: • Variables: • static environment maps ¡variable ¡to ¡type ¡ before ¡evaluation • Syntax: ¡sequence ¡of ¡letters, ¡digits, ¡_, ¡not ¡starting ¡with ¡digit • dynamic environment maps ¡variable ¡to ¡value ¡ during ¡evaluation • Type-‑check: ¡ Lookup ¡in ¡current ¡static ¡environment, ¡fail ¡if ¡not ¡found. • Evaluation: ¡Look ¡up ¡value ¡in ¡current ¡dynamic ¡environment • Type-‑check each ¡binding ¡in ¡order: • using ¡ static environment produced ¡by ¡previous ¡bindings • Addition • and ¡extending ¡it ¡with ¡a ¡binding ¡from ¡variable ¡to ¡type • Syntax: ¡ e1 + e2 where ¡ e1 and ¡ e2 are ¡expressions • Type-‑check: • If ¡ e1 : int and ¡ e2 : int , • Evaluate each ¡binding ¡in ¡order: then ¡ e1 + e2 : int • using ¡ dynamic environment produced ¡by ¡previous ¡bindings • Evaluation: • and ¡extending ¡it ¡with ¡a ¡binding ¡from ¡variable ¡to ¡value • If ¡ e1 evaluates ¡ to ¡ v1 and ¡ e2 evaluates ¡ to ¡ v2 , then ¡ e1 + e2 evaluates ¡ to ¡sum ¡of ¡ v1 and ¡ v2 9 10 Type-‑checking ¡expressions Function ¡binding ¡examples 34 : int ~1 : int (* negative one *) fun pow (x : int, y : int) = if y=0 3.14159 : real true : bool false : bool then 1 x : t else x * pow (x,y-1) • if ¡ ¡ t = lookup ¡ x 's ¡type ¡in ¡current ¡static ¡environment e1 + e2 : int fun cube (x : int) = • if e1 : int and ¡ e2 : int in ¡current ¡static ¡environment pow (x,3) e1 < e2 : bool • if e1 : int and ¡ e2 : int in ¡current ¡static ¡environment val sixtyfour = cube 4 if e1 then e2 else e3 : t • if e1 : bool and ¡ e2 : t and e3 : t in ¡current ¡static ¡environment val fortytwo = • (e2 and ¡ e3 must ¡have ¡the ¡same ¡type) pow (2,2+2) + pow (4,2) + cube (2) + 2 e1 = e2 : bool e1 <> e2 : bool (* not equal *) • if e1 : t and ¡ e2 : t in ¡current ¡static ¡environment • (e2 and ¡ e3 must ¡have ¡the ¡same ¡type, ¡one ¡more ¡restriction ¡later) 11 12 3
9/29/15 Watch ¡out Function ¡bindings • Syntax: fun x0 ( x1 : t1 , … , xn : tn ) = e Odd ¡error ¡messages ¡ for ¡function-‑argument ¡syntax ¡errors • x0 ... xn are ¡variable ¡names • t1 ... tn are ¡types * in ¡type ¡syntax ¡is ¡not ¡arithmetic • e is ¡an ¡expression • Example: ¡ int * int -> int • (Will ¡generalize ¡later) • In ¡expressions, ¡ * is ¡multiplication: ¡ x * pow(x,y-1) • Type-‑check: • Adds ¡binding ¡ x0 : (t1 * … * tn) -> t to ¡current ¡static ¡environment ¡if: Cannot ¡refer ¡ to ¡later ¡function ¡bindings • Can ¡type-‑check ¡body ¡ e to ¡have ¡type ¡ t in ¡the ¡current ¡static ¡environment, ¡ • Helper ¡functions ¡must ¡come ¡before ¡their ¡uses extended ¡with: (arguments ¡ with ¡their ¡ types) • Special ¡construct ¡for ¡ mutual ¡recursion (later) • x1 : t1, …, x n : tn • x0 : (t1 * … * tn) -> t (for ¡recursion) ¡ • Evaluation: • Produce ¡a ¡function ¡closure ¡ c capturing ¡the ¡function ¡code ¡and ¡the ¡current ¡ dynamic ¡environment ¡extended ¡with ¡ x0 à c à • Extend ¡the ¡current ¡dynamic ¡env ironment ¡with ¡ x0 à à c 13 14 Function ¡types Function ¡call fun x0 ( x1 : t1 , … , xn : tn ) = e A ¡new ¡kind ¡of ¡expression: ¡ 3 ¡questions • Function ¡types: ¡ (t1 * … * tn) -> t • Result ¡type ¡on ¡right e0 (e1,…,en) Syntax: ¡ • Overall ¡type-‑checking ¡result: give ¡ x0 this ¡type ¡in ¡rest ¡of ¡program • e0 ... en are ¡ expressions • (Will ¡generalize ¡later . Parentheses ¡optional ¡if ¡exactly ¡one ¡argument.) • Calling ¡ x0 returns ¡result ¡ of ¡evaluating ¡ e , ¡thus ¡return ¡type ¡of ¡ ¡ Type-‑check: ¡ x0 is ¡type ¡of ¡ e. • If: • e0 has ¡some ¡type ¡ (t1 * … * tn) -> t • Type-‑checker ¡ infers ¡ t if ¡such ¡a ¡ t exists. ¡ ¡Later: • e1 has ¡type ¡ t1 , ¡ ¡ ¡…, ¡ ¡ ¡ ¡ en has ¡type ¡ tn • Requires ¡some ¡cleverness ¡due ¡to ¡recursion • Then: • Can ¡omit ¡argument ¡types ¡too • e0(e1,…,en) has ¡type ¡ t Example: ¡ pow(x,y-1) in ¡previous ¡example ¡has ¡type ¡ int 15 16 4
Recommend
More recommend