ten
play

ten other beams & pinned frames Pinned Frames 2 Elements of - PowerPoint PPT Presentation

Nov 23, 2023 •208 likes •286 views

E LEMENTS OF A RCHITECTURAL S TRUCTURES : Continuous Beams F ORM, B EHAVIOR, AND D ESIGN ARCH 614 statically indeterminate D R. A NNE N ICHOLS reduced moments than simple beam S PRING 2018 lecture ten other beams & pinned frames

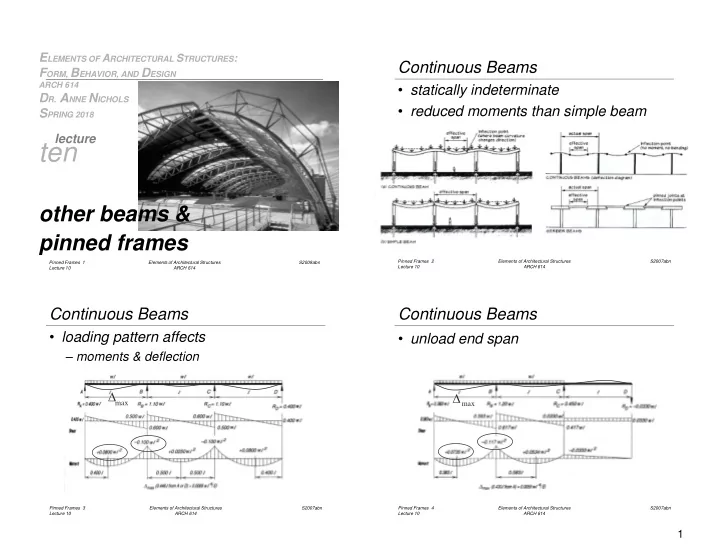
  1. E LEMENTS OF A RCHITECTURAL S TRUCTURES : Continuous Beams F ORM, B EHAVIOR, AND D ESIGN ARCH 614 • statically indeterminate D R. A NNE N ICHOLS • reduced moments than simple beam S PRING 2018 lecture ten other beams & pinned frames Pinned Frames 2 Elements of Architectural Structures S2007abn Pinned Frames 1 Elements of Architectural Structures S2009abn Lecture 10 ARCH 614 Lecture 10 ARCH 614 Continuous Beams Continuous Beams • loading pattern affects • unload end span – moments & deflection   max max Pinned Frames 3 Elements of Architectural Structures S2007abn Pinned Frames 4 Elements of Architectural Structures S2007abn Lecture 10 ARCH 614 Lecture 10 ARCH 614 1

  2. Continuous Beams Moment Redistribution • unload middle span • continuous slabs & beams with uniform loading – joints similar to fixed ends, but can rotate 2 • change in moment to center = wL  max – M max for simply supported beam 8 Pinned Frames 6 Elements of Architectural Structures S2007abn Pinned Frames 5 Elements of Architectural Structures S2007abn Lecture 10 ARCH 614 Lecture 10 ARCH 614 Moment Distribution (a) Moment Distribution (b) • no load • add load http:// nisee.berkeley.edu/godden http:// nisee.berkeley.edu/godden Pinned Frames 7 Elements of Architectural Structures S2007abn Pinned Frames 8 Elements of Architectural Structures S2007abn Lecture 10 ARCH 614 Lecture 10 ARCH 614 2

  3. Moment Distribution Method (c) Moment Distribution Method (d) • release joint 2 • release joint 3 http:// nisee.berkeley.edu/godden http:// nisee.berkeley.edu/godden Pinned Frames 9 Elements of Architectural Structures S2007abn Pinned Frames 10 Elements of Architectural Structures S2007abn Lecture 10 ARCH 614 Lecture 10 ARCH 614 Moment Distribution Method (e) Analysis Methods • exposure of final shape after cycles over • Approximate Methods initial shape – location of inflection points • Force Method – forces are unknowns • Displacement Method – displacements are unknowns http:// nisee.berkeley.edu/godden Pinned Frames 11 Elements of Architectural Structures S2007abn Pinned Frames 12 Elements of Architectural Structures S2007abn Lecture 10 ARCH 614 Lecture 10 ARCH 614 3

  4. Theorem of Three Moments Two Span Beams & Charts • moments at three adjacent supports • equal spans & symmetrical loading (2 spans) • middle support as flat slope • distributed load and same I: 3 3   w L w L       1 1 2 2 M L 2 M L L M L 1 1 2 1 2 3 2 4 4 • concentrated loads and same I:       2 M L M L L M L     1 1 2 1 2 3 2       2 3 2 3 P L n n P L n n 1 1 1 1 2 2 2 2 Pinned Frames 13 Elements of Architectural Structures S2007abn Pinned Frames 14 Elements of Architectural Structures S2007abn Lecture 10 ARCH 614 Lecture 10 ARCH 614 Pinned Frames Rigid Frames • rigid frames have • structures with at least one 3 force body no pins • connected with pins • frame is all one • reactions are equal and opposite body – non-rigid – rigid • typically statically indeterminate • types – portal – gable Pinned Frames 15 Elements of Architectural Structures S2007abn Pinned Frames 16 Elements of Architectural Structures S2007abn Lecture 10 ARCH 614 Lecture 10 ARCH 614 4

  5. Rigid Frames with PINS Internal Pin Connections • frame pieces with • statically determinant connecting pins – 3 equations per body • not necessarily – 2 reactions per pin + support forces symmetrical B G C E F A D A x A y D Pinned Frames 17 Elements of Architectural Structures S2007abn Pinned Frames 18 Elements of Architectural Structures S2007abn Lecture 10 ARCH 614 Lecture 10 ARCH 614 Arches Arches • ancient • primarily sees compression • traditional shape to • a brick “likes an arch” span long distances Packhorse Bridge, UK Rainbow Bridge National Monument Roman Aquaducts Pinned Frames 19 Elements of Architectural Structures S2007abn Pinned Frames 20 Elements of Architectural Structures S2007abn Lecture 10 ARCH 614 Lecture 10 ARCH 614 5

  6. Arches Three-Hinged Arch • behavior • statically determinant – thrust related – 2 bodies, 6 equilibrium equations to height to width – 4 support, 2 pin reactions (= 6) – funicular: to load Pinned Frames 21 Elements of Architectural Structures S2007abn Pinned Frames 22 Elements of Architectural Structures S2007abn Lecture 10 ARCH 614 Lecture 10 ARCH 614 Beams with Internal Pins Procedure • statically determinant when • solve for all support forces you can – 3 equilibrium equations per link => • draw a FBD of each member – total of support & pin reactions – pins are integral with member (properly constrained) – pins with loads should belong to 3+ force • zero moment at pins bodies – pin forces are equal and opposite on F 1 F 2 F 1 F 2 connecting bodies M R1 R 2x R 1x R 2x – identify 2 force bodies vs. 3+ force bodies (internal) pin R 2y R 2y – use all equilibrium equations R 1y R 3 not independent Pinned Frames 23 Elements of Architectural Structures S2007abn Pinned Frames 24 Elements of Architectural Structures S2007abn Lecture 10 ARCH 614 Lecture 10 ARCH 614 6

  7. 7

Recommend

More recommend