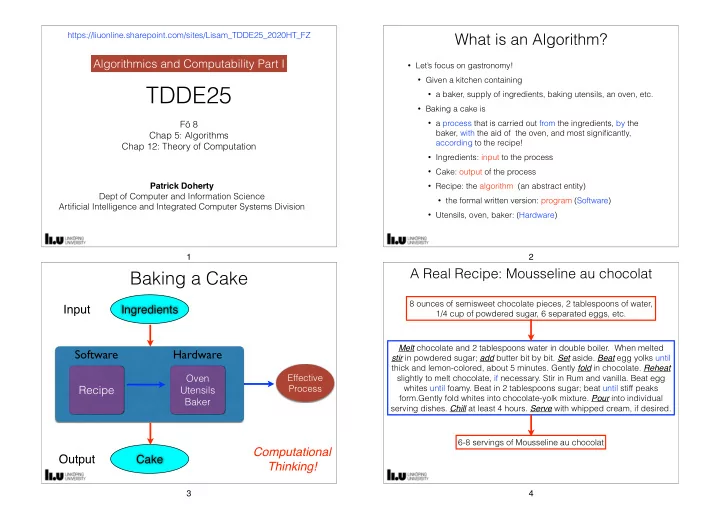

https://liuonline.sharepoint.com/sites/Lisam_TDDE25_2020HT_FZ What is an Algorithm? Algorithmics and Computability Part I • Let’s focus on gastronomy! • Given a kitchen containing TDDE25 • a baker, supply of ingredients, baking utensils, an oven, etc. • Baking a cake is • a process that is carried out from the ingredients, by the Fö 8 baker, with the aid of the oven, and most significantly, Chap 5: Algorithms according to the recipe! Chap 12: Theory of Computation • Ingredients: input to the process • Cake: output of the process Patrick Doherty • Recipe: the algorithm (an abstract entity) Dept of Computer and Information Science • the formal written version: program (Software) Artificial Intelligence and Integrated Computer Systems Division • Utensils, oven, baker: (Hardware) 1 2 A Real Recipe: Mousseline au chocolat Baking a Cake 8 ounces of semisweet chocolate pieces, 2 tablespoons of water, Input Ingredients 1/4 cup of powdered sugar, 6 separated eggs, etc. Melt chocolate and 2 tablespoons water in double boiler. When melted Software Hardware stir in powdered sugar; add butter bit by bit. Set aside. Beat egg yolks until thick and lemon-colored, about 5 minutes. Gently fold in chocolate. Reheat Oven Effective slightly to melt chocolate, if necessary. Stir in Rum and vanilla. Beat egg Process whites until foamy. Beat in 2 tablespoons sugar; beat until stiff peaks Recipe Utensils form.Gently fold whites into chocolate-yolk mixture. Pour into individual Baker serving dishes. Chill at least 4 hours. Serve with whipped cream, if desired. 6-8 servings of Mousseline au chocolat Computational Output Cake Thinking! 3 4
Level of Detail: Basic Actions Short Algorithmic Representations for Long Processes Problem: Basic action because it is assumed “Stir in powdered sugar” Given a list of personnel records, one for each employee in a certain the hardware knows how to do it. company, each containing the employee’s name, personal details, and salary, find the total sum of all salaries of all employees Level of detail is very important when it comes to an Algorithm: algorithm’s elementary instructions. 1. Make a note of the number 0; 2. proceed through the list, adding each employee’s salary to the noted • Should be tailored to fit the hardware’s capabilities number; • Should also be appropriate for the comprehension level 3. having reached the end of the list, produce the noted number as output. of the potential reader or user of the algorithm. The text of the algorithm is short and fixed, yet the process it invokes Ambiguities or Fuzzy Phrases not allowed varies with the length of the input list and can be very, very long! in specifying instructions to a computer! We have: A fixed algorithm prescribing many processes of varying lengths, “about 5 minutes” “served with whipped cream if desired” the precise duration and nature of the process being dependent Is it the serving or addition of WC on the inputs to the algorithm. that is dependent on person’s desires? In fact, the potential choice of inputs may be infinite! 5 6 The Algorithmic Problem and its Solution The Algorithmic Problem and its Solution • An algorithmic problem consists of: Any legal input Characterization of all • a characterization of a legal, possibly infinite, collection of potential legal inputs input sets, and • a specification of the desired outputs as a function of the inputs • Assumption and Algorithm A • a description of allowed basic actions or a hardware configuration, together with its built-in basic actions is provided in advance. Characterization of • Each of the actions must be carried out in a finite amount of time. desired outputs as a • An algorithmic solution consists of: function of inputs Desired Output • an algorithm, composed of elementary instructions prescribing actions from the agreed upon set Algorithmic Algorithmic • the algorithm, when executed for any legal input set, solves the Problem problem, producing the output as required. Solution 7 8
Solving Algorithmic Problems Course Book: Definition of an Algorithm • Algorithmic problems can be incredibly An algorithm is an ordered set of unambiguous finitely complex and take years of work to solve executable steps that defines a terminating process satisfactorily • Many problems do not admit satisfactory solutions An algorithm must contain control instructions that determine the sequence or order in which the • Many problems do not admit solutions at all! executable steps or instructions are carried out • For many problems, the status as far as good algorithmic solutions is still unknown. 9 10 Control Flow or Ordering in Program Execution Control Flow or Ordering in Program Execution cont’d • Concurrency: Two or more program fragments are to be executed/evaluated • Sequencing: Statements are to be executed (or expressions evaluated) “at the same time” in a certain specified order. • either in parallel on separate processors, • Selection: Depending on some runtime condition, a choice is to be • or interleaved on a single processor in a way that achieves the same effect. made among two or more statements or expressions • Exception handling and speculation: A program fragment is executed • The most common selection constructs are if and case (switch) optimistically, on the assumption that the expected condition will be true. If the • Iteration: A given fragment of code is executed repeatedly, either a condition turns out to be false certain number of times, or until a certain run-time condition is true. • execution branches to a handler that executes in place of the remainder of • Iteration constructs include for/do , while , and repeat loops the protected fragment ( in the case of exception handling), or • Procedural Abstraction: A potentially complex collection of control • in place of the entire protected fragment (in the case of speculation) constructs ( a subroutine) is encapsulated in a way that allows it to be • In this case, the language implementation must be able to rollback or treated as a single unit, usually subject to parameterization undo any visible effects of the protected code. • Recursion: An expression is defined in terms of (simpler versions of ) • Nondeterminacy: The ordering or choice among expressions or statements is itself, either directly or indirectly deliberately left unspecified, implying that any alternative will lead to correct • the computational model requires a stack on which to save results. information about partially evaluated instances of the expression. 11 12
Control Flow or Ordering in Program Execution cont’d Computational Problems • These 8 principle categories cover all the • An “algorithm” is an informal intuitive concept, but associated with it is the concept of a computational process. control-flow constructs and mechanisms found • Many attempts have been made to provide formal definitions of what in most programming languages the most general mathematical notion of a computational process is. • Though the syntax and semantics details vary • In other words, a formal equivalent of the informal notion of an from language to language, thinking in these algorithm. terms will make it easier to • For example: • A Turing machine that halts on all inputs is the precise formal • learn new languages notion corresponding to the intuitive notion of an algorithm. • evaluate the tradeoffs among languages • The area that studies such issues is called Computability Theory • It asks the fundamental question: • and design and reason about algorithms in a • What can be computed by a computational device? language-independent way! 13 14 Computational Problems Computational Problems that CANNOT be solved by any algorithm Computability Theory Computational Problems that CAN be solved by an algorithm Computability Theory Computational Problems that CAN be solved by an algorithm Intractable Class NP CANNOT be solved in any practical sense due to excessive time/space Computational requirements Complexity Theory CAN be solved in a practical sense with reasonable time/space Class P Tractable requirements 15 16
Leibniz (1646-1716) Calculus Ratiocinator Some History and • A universal artificial mathematical language • All human knowledge could be represented Context in this language • Calculational rules would reveal all logical relationships among these propositions Let us • Machines would be capable of carrying out such calculations Calculate! Addition Subtraction Multiplication Square root extraction Binary Arithmetic 17 18 Boole (1815 - 1864) Hilbert (1862 - 1943) 1st Problem: Decide the truth of Cantor’s Continum Hypothesis Turned “Logic” into Algebra Classes and terms (thoughts) could be manipulated 2nd Problem: Establish the consistency of the using algebraic rules resulting in valid inferences axioms for the arithmetic of real numbers Logical deduction could Boolean Logic 24 problems be developed as a branch for the of mathematics 20th century Subsumed Aristotle’s syllogisms In essence Leibniz’ 23rd Problem : Does there exist an algorithm that can calculus rationator (lite) determine the truth or falsity of any logical proposition in a system of logic that is powerful enough to represent the natural numbers? (Entscheidungsproblem) 19 20
Recommend
More recommend