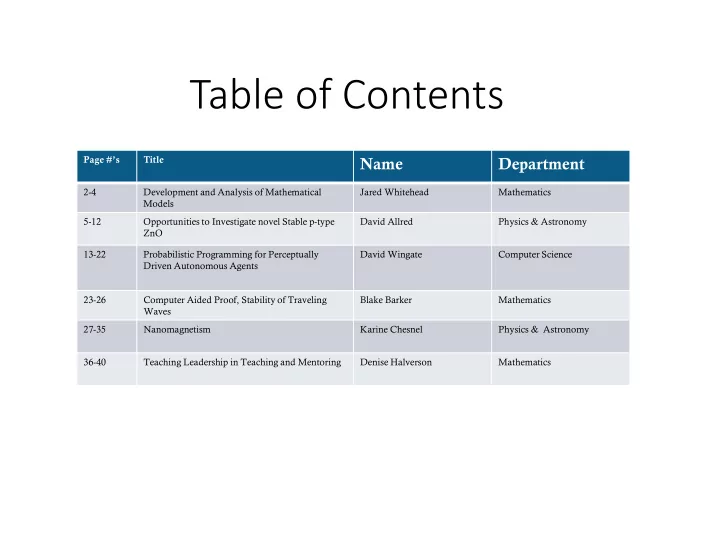
Table of Contents Page #s Title Name Department 2-4 Development - PowerPoint PPT Presentation

Table of Contents Page #’s Title Name Department 2-4 Development and Analysis of Mathematical Jared Whitehead Mathematics Models 5-12 Opportunities to Investigate novel Stable p-type David Allred Physics & Astronomy ZnO 13-22 Probabilistic Programming for Perceptually David Wingate Computer Science Driven Autonomous Agents 23-26 Computer Aided Proof, Stability of Traveling Blake Barker Mathematics Waves 27-35 Nanomagnetism Karine Chesnel Physics & Astronomy 36-40 Teaching Leadership in Teaching and Mentoring Denise Halverson Mathematics

Development and Analysis of Mathematical Models Jared P. Whitehead Mathematics Department whitehead@mathematics.byu.edu Picture courtesy of Zhao Pan.

Topics of recent interest:  Rigorous estimates (bounds) on physically interesting statistical quantities in fluid dynamics.  Quantification and validation of long-time dynamics of climate, weather, and ocean modeling.  Aspects of linear, and nonlinear stability theory applied to finite and infinite dimensional stochastic dynamical systems.  Mathematical modeling and the analysis of mathematical models in the physical and social sciences .

Of far more interest... We are starting a mathematical modeling center this fall This means a bunch of mathematicians (with quantitatively skilled students to boot) want to hear about your problems. If you have a modeling issue, or have something that you think some mathematicians may be able to help with, please get in touch with me and we'll put you on the calendar! whitehead@mathematics.byu.edu

Opportunities to Investigate novel Stable p-type ZnO: Making progress with the Asymmetric dopant problem David Allred Physics and Astronomy allred@byu.edu (801) 422-3489 Areas of Interest: Thin films, Extreme Ultraviolet Optics, Nanostructures-MEMS, Mars Simulations, Alternate Energy Issues (Solar, Batteries, etc.) 5

Opportunities to Investigate novel Stable p-type ZnO: Making progress with the Asymmetric dopant problem From Zeno

Mater erial als S Scien ence: T The A e Asymmetric D Dop opan ant P Prob oblem em • For over 60 years p-type Wide-bandgap semiconductors have been a problem. • ZnO has been described as a very desirable semiconductor materials. • How to make stable forms of moderate to heavily p-type semiconductors, • For example, for zinc-oxide this elusive goal has been driven by the material’s desirable electronic, thermal, and mechanical properties. • The traditional approach seems unlikely to succeed due to compound stability and vapor pressure constraints on diffusional processes. Diffusion couples cannot be used to create long-term stable p-type zinc oxides. • One technical team succeeded in producing stable p-type ZnO materials in 2007 , produced over a range of dopant levels, from 10 15 to 10 21 atoms per cm 3 . By XPS arsenic concentrations at 0.25%, down a depth of 250 µm. “… this material I tested [Zeno Material’s p-type ZnO] is already good enough to produce good p-n junctions. The realization of a good, reliable, reproducible p-n junction in ZnO will cause an explosion of commercial interest .” David Look, Ph.D., Director, Semiconductor Research Center – USAF Zeno Materials LLC

What is the problem? Simply it is that atoms tend to go where they want to go not where the design would have them go.

Innovation: New S Semiconductor M Material S Syst ystem Traditional fabrication methods of p-type ZnO have failed for decades to produce stable electronic materials. Zeno’s fabrication approach does not use dopant diffusion or ion implantation, it is fundamentally different to traditional methods. Dopants are essentially fixed within the unit cell. Zeno’s technology enables p-type ZnO fabrication that is inexpensive, controllable and reproducible. The process yields highly stable materials, with over 7 years of confirmed stability. Zeno brings together seemingly The process does not incompatible elements rely on diffusion or ion implantation Sputter onto Producing highly stable dopants in ZnO a hot substrate Zeno Materials LLC

Interesting C Charact cteristics cs: Stability & & Mobility P-type ZnO Stability comparison: P-Type carrier mobility: Zeno vs. best performing conventionally fabricated a-Silicon vs. Zeno P-type Charge Carrier Concentration / cm 3 10 20 Zeno Materials 1 10 19 Zeno 10 18 cm 2 • v olt -1 • sec -1 10 17 10 16 Best known competitor 2 10 15 0 1 2 3 4 5 6 7 Years a-Silicon 3 1 Arsenic doped ZnO fabricated by Zeno Materials, sample was left in storage without sealant or special handling exposed to ambient air.. Hole mobility often limits overall mobility 2 Nitrogen doped ZnO, Fig.12, "Stability Studies on Nitrogen Doped p-ZnO (NZO) Thin Films and semiconductor performance. The Grown by Reactive Magnetron Sputtering". R.V. Muniswami Naidu et al, Journal of Display Technology, Vol.9, No.9, Sept. 2013 Company’s materials provide a hole 3 "ZnO Devices and Applications" Özgür et al (2010) mobility of about 220 cm 2 /volt•sec, nearly equal to that of the electron mobility. Zeno Materials LLC

Strategy: prod oduces es s stab able p e p-type Z ZnO Equations: (As O ) Oxygen 0 1 Arsenic substitution on an oxygen site: ZnO 1-x + As x = 1 0.8 0.2 Oxygen - Arsenic General equation* for “compounds”: Zinc - Oxygen [Zn 4 O 4-n + As n ] = 1 For n= 0 to 4 0.4 0.6 n=0: Zn 4 O 4 Consequences: 0.6 0.4 n=1: [Zn 4.5 O 3 As] • Only specific stoichiometric compositions are stable within the ternary diagram 0.8 0.2 n=2: [Zn 5 O 2 As 2 ] • Other dopants besides Arsenic are viable n=3: [Zn 5.5 OAs 3 ] 1 0 Arsenic Zinc n=4: [Zn 3 As 2 ] 0 0.2 0.4 0.6 0.8 1 Zinc - Arsenic Dotted Line Indicates No Compositions Between Data Points * Assuming 2 unit cells with ZnO and Zn 3 As 2 as compositional endpoints. Zeno Materials LLC

Material A Applications: p-ty type Z ZnO Since the 1960s, p-type ZnO has been pursued for its predicted properties, which include: • Direct wide bandgap semiconductor • High thermal operating range ( exciton binding energy ~60 meV ) • Radiation resistant semiconductor • Can be doped as an emitter between ~160 nm* to ~500 nm • Emitters can also be detectors P-type ZnO made by Zeno • Materials (~10 19 p-type carriers, Solid state light source ρ = 0.008 Ω -cm) ** on undoped Si. • Limited stacking faults, dislocations, and other crystal defects • ZnO self-organizes into resonator cavities that readily emit laser light (on silicon wafer coated with Ti and Au thin films) * Allowing for a single frequency doubling ** As measured by Dr. David Look – Wright-Patterson AFB (USAF) & Wright State University. Zeno Materials LLC

Probabilistic Programming for Perceptually Driven Autonomous Agents David Wingate Perception, Control and Cognition Laboratory Computer Science Department wingated@cs.byu.edu

Learning and acting in complex domains • Goal: autonomous agents that perceive, reason and act • Agents must build models of the world that include • object-based perception • causality • structured planning • reasoning about other agents • social cognition • natural language semantics • etc… • How can we do this? • … with code that is evolvable, scalable, maintainable and safe?

Probabilistic Programming and DNNs We need to combine the strengths of two frameworks: Bayesian models and Deep Learning Higher-order perception Acting Reasoning about other agents DNNs are responsible for pixel processing

Social Cognition The principle of rationality : an agent tends to choose actions that she expects to lead to outcomes that satisfy her goals Sally walks up to a vending machine. The machine has two buttons, A and B. A always dispenses chips. B usually dispenses cookies, but will sometimes dispense chips. Sally pushes button B, and gets a bag of chips. What did Sally want? Goodman and Tenenbaum, ProbMods, retrieved 2016

Social Cognition The principle of rationality : an agent tends to choose actions that she expects to lead to outcomes that satisfy her goals Inference must implicitly account for the counterfactual alternatives This sort of reasoning can be formalized with probabilistic models that combine beliefs , desires , goals and plans Goodman and Tenenbaum, ProbMods, retrieved 2016

Social Cognition Goodman and Tenenbaum, ProbMods, retrieved 2016

Summary • Goal: autonomous agents • Evolvable, scalable, maintainable, debuggable, explainable, safe • Must build models of the world • Involving objects, agents, plans, decisions – uncertainty everywhere! • Integrated by virtue of the compositionality of hierarchical Bayesian models • Strategy: combine DNNs and Bayesian models • Delivered as core capabilities of a probabilistic programming language • Drawing on models from cognitive science and ML

Thank you!

Computer Aided Proof, Stability of traveling waves Blake Barker Department of Mathematics blake@mathematics.byu.edu

Computer Aided Proof  Track all errors in a computation  Use high level mathematics  Find truncation error of method  Bound machine truncation error with intervals 

Stability of traveling waves  Water waves  Detonation waves  MHD waves Roll Waves  Waves in gas dynamics  Microtubule formation

Blake Barker Department of Mathematics blake@mathematics.byu.edu