t w c
play

T w + C Minimize T z fo r some Z spae N 1 n 2 w n =1 K - PowerPoint PPT Presentation

Sep 18, 2022 •194 likes •405 views

Review of Leture 15 Soft-ma rgin SVM Kernel metho ds T w + C Minimize T z fo r some Z spae N 1 n 2 w n =1 K ( x , x ) = z Hi Hi violation Same as ha rd ma rgin, but 0 n C Hi Hi

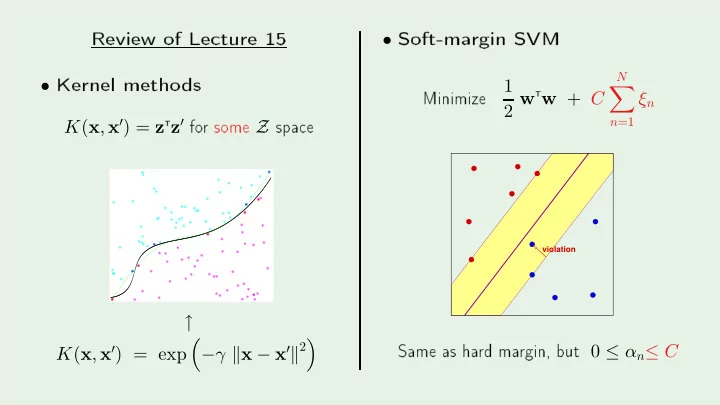
  1. Review of Le ture 15 Soft-ma rgin SVM Kernel metho ds T w + C Minimize • T z ′ fo r some Z spa e N • 1 � ξ n 2 w n =1 K ( x , x ′ ) = z Hi Hi violation Same as ha rd ma rgin, but 0 ≤ α n ≤ C Hi ↑ Hi � − γ � x − x ′ � 2 � K ( x , x ′ ) = exp

  2. Lea rning F rom Data Y aser S. Abu-Mostafa Califo rnia Institute of T e hnology Le ture 16 : Radial Basis F un tions Sp onso red b y Calte h's Provost O� e, E&AS Division, and IST Thursda y , Ma y 24, 2012 •

  3. Outline RBF and nea rest neighb o rs RBF and neural net w o rks • RBF and k ernel metho ds • RBF and regula rization • • Creato r: Y aser Abu-Mostafa - LFD Le ture 16 2/20 M � A L

  4. Basi RBF mo del Ea h ( x n , y n ) ∈ D in�uen es h ( x ) based on � x − x n � radial Standa rd fo rm: � �� � basis fun tion N � − γ � x − x n � 2 � � h ( x ) = w n exp � �� � n =1 Creato r: Y aser Abu-Mostafa - LFD Le ture 16 3/20 M � A L

  5. The lea rning algo rithm Finding w 1 , · · · , w N : N � − γ � x − x n � 2 � � based on D = ( x 1 , y 1 ) , · · · , ( x N , y N ) h ( x ) = w n exp n =1 in = 0 : fo r n = 1 , · · · , N : h ( x n ) = y n E N � − γ � x n − x m � 2 � � w m exp = y n Creato r: Y aser Abu-Mostafa - LFD Le ture 16 4/20 m =1 M � A L

  6. The solution equations in N unkno wns N � − γ � x n − x m � 2 � � w m exp = y n N m =1 . . . . . . . . . . . . . . .       exp( − γ � x 1 − x 1 � 2 ) exp( − γ � x 1 − x N � 2 ) . . . w 1 y 1 exp( − γ � x 2 − x 1 � 2 ) exp( − γ � x 2 − x N � 2 )       . . . w 2 y 2       =             exp( − γ � x N − x 1 � 2 ) exp( − γ � x N − x N � 2 ) w N y N . . . � �� � � �� � � �� � If Φ is invertible, �exa t interp olation� Φ w y Creato r: Y aser Abu-Mostafa - LFD Le ture 16 5/20 w = Φ − 1 y M � A L

  7. The e�e t of γ N � − γ � x − x n � 2 � � h ( x ) = w n exp n =1 small γ la rge γ Creato r: Y aser Abu-Mostafa - LFD Le ture 16 6/20 M � A L

  8. RBF fo r lassi� ation sign � N − γ � x − x n � 2 �� � � Lea rning: ∼ linea r regression fo r lassi� ation h ( x ) = w n exp n =1 N � − γ � x − x n � 2 � � Minimize ( s − y ) 2 on D s = w n exp n =1 sign ( s ) y = ± 1 Creato r: Y aser Abu-Mostafa - LFD Le ture 16 7/20 h ( x ) = M � A L

  9. Relationship to nea rest-neighb o r metho d A dopt the y value of a nea rb y p oint: simila r e�e t b y a basis fun tion: Creato r: Y aser Abu-Mostafa - LFD Le ture 16 8/20 M � A L

  10. RBF with K enters pa rameters w 1 , · · · , w N based on N data p oints Use K ≪ N enters: µ 1 , · · · , µ K instead of x 1 , · · · , x N N K � − γ � x − µ k � 2 � � 1. Ho w to ho ose the enters µ k h ( x ) = w k exp k =1 2. Ho w to ho ose the w eights w k Creato r: Y aser Abu-Mostafa - LFD Le ture 16 9/20 M � A L

  11. Cho osing the enters Minimize the distan e b et w een x n and the losest enter µ k : -means lustering Split x 1 , · · · , x N into lusters S 1 , · · · , S K K Minimize K � � � x n − µ k � 2 Unsup ervised lea rning k =1 x n ∈ S k NP -ha rd Creato r: Y aser Abu-Mostafa - LFD Le ture 16 10/20 M � A L

  12. An iterative algo rithm w.r.t. Llo yd's algo rithm: Iteratively minimize K � � � x n − µ k � 2 µ k , S k x n ∈ S k k =1 1 � µ k ← all � x n − µ ℓ �} x n | S k | x n ∈ S k Convergen e lo al minimum S k ← { x n : � x n − µ k � ≤ − → Creato r: Y aser Abu-Mostafa - LFD Le ture 16 11/20 M � A L

  13. Llo yd's algo rithm in a tion 1. Get the data p oints Hi 2. Only the inputs! 3. Initialize the enters 4. Iterate 5. These a re y our µ k 's Creato r: Y aser Abu-Mostafa - LFD Le ture 16 12/20 Hi M � A L

  14. Centers versus supp o rt ve to rs supp o rt ve to rs RBF enters Hi Hi Creato r: Y aser Abu-Mostafa - LFD Le ture 16 13/20 Hi Hi M � A L

  15. Cho osing the w eights equations in K< N unkno wns K � − γ � x n − µ k � 2 � � w k exp ≈ y n N k =1 . . . . . . . . . . . . . . .       exp( − γ � x 1 − µ 1 � 2 ) exp( − γ � x 1 − µ K � 2 ) . . . w 1 y 1 exp( − γ � x 2 − µ 1 � 2 ) exp( − γ � x 2 − µ K � 2 )       . . . w 2 y 2       ≈             exp( − γ � x N − µ 1 � 2 ) exp( − γ � x N − µ K � 2 ) w K y N . . . T Φ T Φ) − 1 Φ T y � �� � � �� � � �� � If Φ is invertible, pseudo-inverse Φ w y Creato r: Y aser Abu-Mostafa - LFD Le ture 16 14/20 w = (Φ M � A L

  16. RBF net w o rk The �features� a re h ( x ) Nonlinea r transfo rm dep ends on D � − γ � x − µ k � 2 � exp ↑ No longer a linea r mo del b − → w 1 w K w k = ⇒ · · · · · · φ φ φ � x − µ k � � x − µ 1 � � x − µ K � A bias term ( b o r w 0 ) is often added x Creato r: Y aser Abu-Mostafa - LFD Le ture 16 15/20 M � A L

  17. Compa re to neural net w o rks h ( x ) h ( x ) ↑ ↑ w 1 w 1 w K w K w k w k T T T · · · · · · · · · · · · φ φ φ θ θ θ � x − µ k � w k x � x − µ 1 � � x − µ K � RBF net w o rk neural net w o rk w 1 x w K x x x Creato r: Y aser Abu-Mostafa - LFD Le ture 16 16/20 M � A L

  18. Cho osing γ T reating γ as a pa rameter to b e lea rned K � − γ � x − µ k � 2 � � h ( x ) = w k exp Iterative app roa h ( ∼ EM algo rithm in mixture of Gaussians): k =1 1. Fix γ , solve fo r w 1 , · · · , w K 2. Fix w 1 , · · · , w K , minimize erro r w.r.t. γ W e an have a di�erent γ k fo r ea h enter µ k Creato r: Y aser Abu-Mostafa - LFD Le ture 16 17/20 M � A L

  19. Outline RBF and nea rest neighb o rs RBF and neural net w o rks • RBF and k ernel metho ds • RBF and regula rization • • Creato r: Y aser Abu-Mostafa - LFD Le ture 16 18/20 M � A L

  20. RBF versus its SVM k ernel SVM k ernel implements: Hi sign   SVM � − γ � x − x n � 2 �  � α n y n exp + b  Straight RBF implements: RBF α n > 0 sign � � K � − γ � x − µ k � 2 � � w k exp + b Creato r: Y aser Abu-Mostafa - LFD Le ture 16 19/20 k =1 Hi M � A L

  21. RBF and regula rization RBF an b e derived based purely on regula rization: � ∞ ∞ � d k h � 2 N � 2 + λ � � � h ( x n ) − y n a k dx �smo othest interp olation� dx k −∞ n =1 k =0 Creato r: Y aser Abu-Mostafa - LFD Le ture 16 20/20 M � A L

Recommend

More recommend