Syntax and grammars, more datatypes, Source Program Break up - PowerPoint PPT Presentation

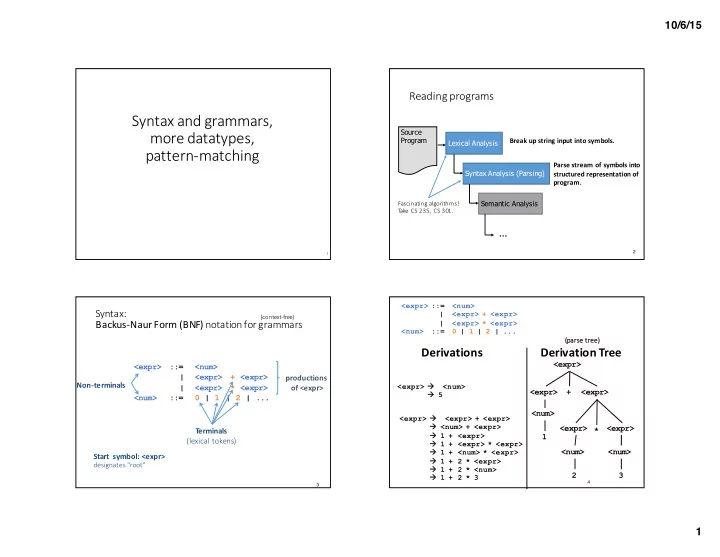
10/6/15 Reading ¡programs Syntax ¡and ¡grammars, more ¡datatypes, Source ¡ Program Break ¡up ¡string ¡input ¡into ¡symbols. Lexical ¡Analysis pattern-­‑matching Parse ¡stream ¡of ¡symbols ¡into ¡ Syntax ¡Analysis ¡(Parsing) structured ¡representation ¡of ¡ program. Semantic ¡Analysis Fascinating ¡algorithms! T ake ¡ CS ¡235, ¡CS ¡301. ... 2 1 <expr> ::= <num> Syntax: | <expr> + <expr> (context-­‑free) Backus-­‑Naur ¡Form ¡(BNF) notation ¡for ¡grammars | <expr> * <expr> <num> ::= 0 | 1 | 2 | ... (parse ¡ (p ¡tree) Derivations Derivation ¡Tree <expr> <expr> ::= <num> | <expr> + <expr> productions Non-­‑terminals of ¡<expr> <expr> à à <num> | <expr> * <expr> <expr> + <expr> à 5 à <num> ::= 0 | 1 | 2 | ... <num> à à <expr> <expr> + <expr> à à <num> + <expr> <expr> <expr> T erminals * à 1 + <expr> à 1 (lexical ¡tokens) à 1 + <expr> à * <expr> à 1 + <num> à <num> <num> * <expr> Start ¡ symbol: ¡<expr> à 1 + 2 * <expr> à designates ¡"root" à 1 + 2 * <num> à 2 3 à 1 + 2 * 3 à 4 3 1

10/6/15 <expr> à <expr> * <expr> Ambiguity: à <expr> * <num> à <expr> * 3 >1 >1 ¡ ¡derivation ¡ ¡of ¡ ¡expressi ssion Dealing ¡with ¡Ambiguity à <expr> + <expr> * 3 <expr> ::= <num> à <num> + <expr> * 3 | <expr> + <expr> à 1 + <expr> * 3 | <expr> * <expr> à 1 + <num> * 3 Prohibit ¡it. <num> ::= 0 | 1 | 2 | ... à 1 + 2 * 3 Force ¡parenthesization or ¡equivalent. <expr> <expr> Racket, ¡S-­‑expressions: (there is (always an unambiguous) parse tree) <expr> + <expr> <expr> * <expr> Allow ¡it ¡with: Precedence by ¡kind ¡of ¡expression ¡(think ¡ order ¡of ¡operations ) 1 + 2 * 3 means ¡ 1 + (2 * 3) <num> <num> Directional ¡ associativity (left, ¡right) <expr> <expr> <expr> <expr> left-­‑associative ¡ function ¡ application: ¡ f 2 3 means ¡ ((f 2) 3) * + 1 3 <num> <num> <num> <num> 2 3 1 2 5 Abstract ¡Syntax ¡Trees ¡(ASTs) ¡in ¡ML Recursive ¡functions ¡for ¡recursive ¡datatypes (or ¡expression ¡ trees) Find ¡maximum ¡ constant ¡appearing ¡in ¡an ¡expression. A ¡tiny ¡calculator ¡language: (Program ¡analysis ¡for ¡our ¡tiny ¡language!) datatype exp = Constant of int | Negate of exp fun max_constant (e : exp) = | Add of exp * exp | Multiply of exp * exp An ¡expression ¡in ¡ML ¡of ¡type ¡ exp : ¡ Add (Constant (10+9), Negate (Constant 4)) How ¡to ¡picture ¡the ¡resulting ¡value: ¡ Add Constant Negate Constant 19 7 8 4 Derived ¡from ¡ slides ¡due ¡to ¡Dan ¡Grossman 2

10/6/15 Evaluating ¡expressions ¡in ¡the ¡language Datatypebindings, ¡so ¡far We ¡have ¡defined ¡a ¡tiny ¡calculator ¡programming ¡language. Syntax : ¡ datatype t = C1 of t1 | C2 of t2 | … | Cn of tn Let's ¡write ¡an ¡interpreter ¡for ¡it! Type-­‑checking : fun eval (e : exp) = Adds ¡type ¡ t and ¡constructors ¡ Ci of ¡type ¡ ti->t to ¡static ¡ environment • Ci v is ¡a ¡value, ¡i.e., ¡the ¡result ¡“includes ¡the ¡tag” Evaluation : ¡nothing! Omit ¡“ of t ” ¡for ¡constructors ¡that ¡are ¡just ¡tags, ¡no ¡underlying ¡data • Such ¡a ¡ Ci is ¡a ¡value ¡of ¡type ¡ t 9 10 Case ¡expressions, ¡so ¡far Case ¡expressions, ¡so ¡far Syntax: case e of p1 => e1 | p2 => e2 | … | pn => en Syntax: case e of p1 => e1 | p2 => e2 | … | pn => en Type-­‑checking: Evaluation: • Type-­‑check ¡ e. ¡ ¡Must ¡have ¡same ¡type ¡as ¡all ¡of ¡ p1 ... pn . • Evaluate ¡ e to ¡a ¡value ¡ v • Pattern ¡ C(x1,…,xn) has ¡type ¡ t if ¡datatype t includes ¡a ¡ • If ¡ pi is ¡first ¡ pattern to ¡ match v , ¡then ¡result ¡is ¡evaluation ¡ constructor: ¡ C of t1 * ... * tn of ¡ ei in ¡dynamic ¡environment ¡ “extended ¡by ¡the ¡match.” • Type-­‑check ¡ each ¡ ei in ¡current ¡static ¡environment ¡ • Pattern ¡ Ci(x1,…,xn) matches ¡value ¡ extended ¡ with ¡types ¡for ¡any ¡variables ¡ bound ¡by ¡ pi . Ci(v1,…,vn) and ¡extends ¡the ¡environment ¡ by ¡ • Pattern ¡ C(x1,…,xn) gives ¡variables ¡ x1 , ¡..., ¡ xn types ¡ t1 ,..., tn if ¡ binding ¡ x1 to ¡ v1 … ¡ xn to vn datatype t includes ¡a ¡constructor: ¡ C of t1 * ... * tn • For ¡“no ¡data” ¡constructors, ¡pattern ¡ Ci matches ¡value ¡ Ci • All ¡ ei must ¡have ¡the ¡same ¡type ¡ u , ¡which ¡is ¡the ¡type ¡of ¡the ¡ • Pattern ¡ x matches ¡and ¡binds ¡to ¡any ¡value ¡ of ¡any ¡type. entire ¡ case ¡expression. • Exception ¡if ¡no ¡pattern ¡matches. 11 12 3

10/6/15 Hold ¡on ¡to ¡your ¡hats! ¡ ¡Deep ¡truths ¡about ¡patterns ¡ahead... Hold ¡on ¡to ¡your ¡hats! Pattern-­‑match ¡any ¡compound ¡type Pattern ¡matching ¡also ¡works ¡for ¡records ¡and ¡tuples: Deep ¡truths ¡about ¡ML ¡and ¡patterns. • Pattern ¡ (x1,…,xn) matches ¡any ¡tuple ¡value ¡ (v1,…,vn) • Every ¡val-­‑binding ¡and ¡function-­‑binding ¡uses ¡ pattern-­‑matching. • Pattern ¡ {f1=x1, …, fn=xn} matches ¡any ¡record ¡value ¡ {f1=v1, …, fn=vn} (and ¡fields ¡can ¡be ¡reordered) • Every ¡function ¡in ¡ML ¡takes ¡exactly ¡one ¡argument First: ¡extend ¡our ¡definition ¡of ¡pattern-­‑matching… 13 14 val-­‑binding ¡patterns Function-­‑argument ¡patterns • Remember ¡ tuple ¡bindings? A ¡function ¡argument ¡is ¡a ¡pattern • Match ¡against ¡the ¡argument ¡in ¡a ¡function ¡call fun f p = e val p = e • A ¡val-­‑binding ¡can ¡use ¡a ¡pattern, ¡not ¡just ¡a ¡variable • Variables ¡are ¡just ¡one ¡kind ¡of ¡pattern. Examples ¡( fantastic ¡style! ): fun sum_triple (x, y, z) = x + y + z • Style: • Get ¡all/some ¡pieces ¡out ¡of ¡a ¡product/each-­‑of ¡type fun full_name {first=x, middle=y, last=z} = • Usually ¡poor ¡style ¡to ¡put ¡constructor ¡pattern ¡in ¡val binding x ^ " " ^ y ^ " " ^ z • Raises ¡ exception ¡if ¡different ¡variant ¡is ¡there. 15 18 4

10/6/15 Convergence! Every ¡ML ¡function ¡takes ¡exactly ¡one ¡argument • "Multi-­‑argument" ¡ functions: T akes ¡ one ¡ int*int*int triple, returns ¡ int that ¡is ¡their ¡sum: • match ¡a ¡tuple ¡pattern ¡against ¡their ¡single ¡argument • Elegant, ¡flexible ¡language ¡design fun sum_triple (x, y, z) = x + y + z • Cute ¡and ¡useful ¡things fun rotate_left (x, y, z) = (y, z, x) T akes ¡ three ¡ int values, ¡returns ¡ int that ¡is ¡their ¡sum: fun rotate_right t = rotate_left(rotate_left t) • “Zero ¡arguments” ¡is ¡the ¡unit ¡pattern ¡ () fun sum_triple (x, y, z) = x + y + z matching ¡the ¡unit ¡value ¡ () 19 20 Even ¡more ¡pattern-­‑matching Patterns ¡are ¡deep! • Patterns ¡are ¡so ¡much ¡fun! • Patterns ¡are ¡recursively ¡ structured • Just ¡like ¡expressions fun eval e = • Nest ¡as ¡deeply ¡as ¡desired case e of • Avoid ¡hard-­‑to-­‑read, ¡wordy, ¡nested ¡case ¡expressions Constant i => i | Negate e2 => ~ (eval e2) • Full ¡meaning ¡ of ¡pattern-­‑matching: | Add (e1,e2) => (eval e1) + (eval e2) | Multiply (e1,e2) => (eval e1) * (eval e2) • compare ¡pattern ¡against ¡value ¡for ¡“same ¡shape” • bind ¡variables ¡to ¡the ¡“right ¡parts” fun eval (Constant i) = i | eval (Negate e2) = ~ (eval e2) • More ¡precise ¡recursive ¡definition ¡after ¡examples | eval (Add (e1,e2)) = (eval e1) + (eval e2) | eval (Multiply (e1,e2)) = (eval e1) * (eval e2) • Note ¡added ¡parens around ¡each ¡pattern, ¡replaced ¡=> ¡with ¡=. • If ¡you ¡mix ¡them ¡up, ¡you'll ¡get ¡some ¡weird ¡error ¡messages... 21 22 5