Supervisor - Task Given Process model, P Specification, K K - PDF document

Department of Signals and Systems Supervisor - Task • Given Process model, P – Specification, K – K Calculate supervisor S •  – Within the spec ( ) ( ) L P S L P K P || S = S  – Non-blocking ( ) ( ) L P S L P S m   – Controllable  ( ) ( ) ( ) L P S L P L P S u   – Max permissive P S P S P • Problem can want – Blocking must – Un-controllable events 32 Martin Fabian Chalmers Automation

Department of Signals and Systems Supervisor - Verification Given P , S and K, verify that • S ”works” properly – K S ”works” • – Controllable P || S ? – Nonblocking P || S fulfills the specification • – Undesired states are avoided P – Undesired strings avoided can want – Language inclusion  ( ) ( ) L P S L P K  ( ) ( ) L P S L P S m    ( ) ( ) ( ) L P S L P L P S u 33 Martin Fabian Chalmers Automation

Department of Signals and Systems Supervisor - Synthesis Iterative calculation, S 0 = P || K • – Forbid undesired states If uncontrollable, make controllable, S i • If blocking, make nonblocking, S i+1 K • • Etc... Terminates at fixpoint , S i = S i+1 – P || S = S Optimality, P || S = S ≤ S 0 • – A unique largest supervisor always exists – Maximally permissive, minimally restrictive P Allows P maximal freedom within the spec – can want must Synthesis can  be viewed as a ( ) ( ) L P S L P K series of  verification ( ) ( ) L P S L P S m tasks    ( ) ( ) ( ) L S L P L S u 34 Martin Fabian Chalmers Automation

Department of Signals and Systems Supervisor – Minimally Retrictive • Calculates sub-automata S 0 – Can be ordered in a structure – Lattice • Unique element exist S 1 S 2 S 3 Unique largest element, S0 – Unique smallest element, 0- – automaton S 4 S 5 • Set of all controllable sub-automata Nonblocking – Has unique largest element, S2 Controllable • Set of all non-blocking sub- automata S 6 – Has unique largest element, S1 • Intersection controllable and non- blocking S 7 =  – Unique largest solution, S4 35 Martin Fabian Chalmers Automation

Department of Signals and Systems Supervisor - Synthesis • Algorithm 1. Calculate T 0 = P||K 2. Find un-controllable K states S 0 = f(P, T 0 ) 3. S i+1 = SupNB(S i ) P || S = S 4. S i+2 = SupC(S i+1 ) 5. If S i+2 ≠ S i+1 , go to 3 6. S := S i+1 P can want must 36 Martin Fabian Chalmers Automation

Department of Signals and Systems Supervisor – Finding Un-controllable States • Synch P||K P – Compare P||K with P !u – If exists uc-event from state p a – Not exist from state <p,q> p0 p1 b Then <p,q> un-controlable state – • Can be done while synching P||K – If uc-event disappears – Mark state as un-controllable a b – State is forbidden p0.q0 p1.q1   ( ) s L P K      ( ( , )) ( ( , )) i s i s u P P u P K P K 37 Martin Fabian Chalmers Automation

Department of Signals and Systems Supervisor - Synthesis • Algorithm 1. Calculate T 0 = P||K 2. Find un-controllable K states S 0 = f(P, T 0 ) 3. S i+1 = SupNB(S i ) P || S = S 4. S i+2 = SupC(S i+1 ) 5. If S i+2 ≠ S i+1 , go to 3 6. S := S i+1 P • Claim: can want – Within spec must We want proof! – Non-blocking – Controllable – Maximally permissive 38 Martin Fabian Chalmers Automation

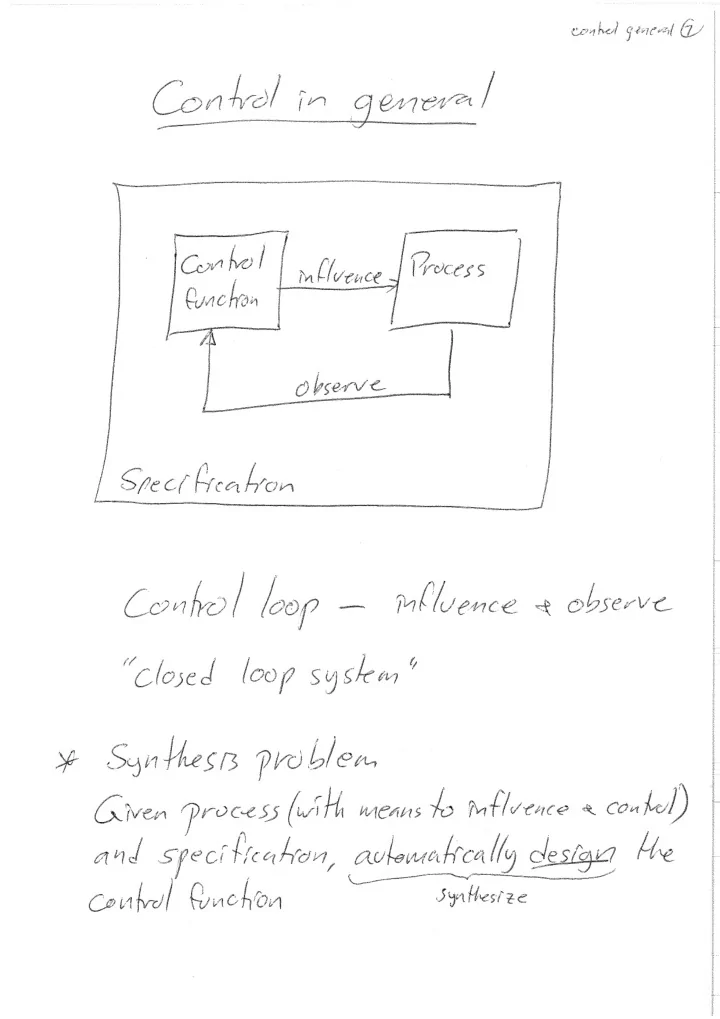
Department of Signals and Systems Supervisor – Monolithic Synthesis • Process typically described by – Interacting sub-processes – P = P 1 || P 2 ||…|| P n – Restrict each other • Spec typically described by – Interacting sub-specs – K = K 1 || K 2 ||…|| K m – Restrict each other • Monolithic supervisor Single one for the entire P and – entire K • Guarantees influence S1 P2 P S3 S – No specs violated S2 P1 observe P3 – But... 39 Martin Fabian Chalmers Automation