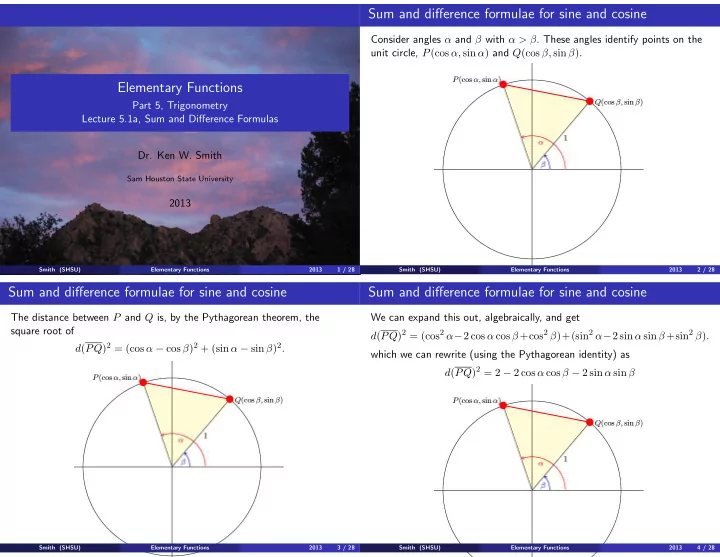
Sum and difference formulae for sine and cosine Consider angles and - PowerPoint PPT Presentation

Sum and difference formulae for sine and cosine Consider angles α and β with α > β. These angles identify points on the unit circle, P (cos α, sin α ) and Q (cos β, sin β ) . Elementary Functions Part 5, Trigonometry Lecture 5.1a, Sum and Difference Formulas Dr. Ken W. Smith Sam Houston State University 2013 Smith (SHSU) Elementary Functions 2013 1 / 28 Smith (SHSU) Elementary Functions 2013 2 / 28 Sum and difference formulae for sine and cosine Sum and difference formulae for sine and cosine The distance between P and Q is, by the Pythagorean theorem, the We can expand this out, algebraically, and get square root of d ( PQ ) 2 = (cos 2 α − 2 cos α cos β +cos 2 β )+(sin 2 α − 2 sin α sin β +sin 2 β ) . d ( PQ ) 2 = (cos α − cos β ) 2 + (sin α − sin β ) 2 . which we can rewrite (using the Pythagorean identity) as d ( PQ ) 2 = 2 − 2 cos α cos β − 2 sin α sin β Smith (SHSU) Elementary Functions 2013 3 / 28 Smith (SHSU) Elementary Functions 2013 4 / 28

Sum and difference formulae for sine and cosine Sum and difference formulae for sine and cosine Let’s rotate this picture clockwise through the angle − β so that the point Q becomes Q ′ (1 , 0) lying on the x -axis. The point P rotates into the point P ′ (cos( α − β ) , sin( α − β )) The distance from P ′ to Q ′ is the same as the distance from P to Q . Smith (SHSU) Elementary Functions 2013 5 / 28 Smith (SHSU) Elementary Functions 2013 6 / 28 Sum and difference formulae for sine and cosine Sum and difference formulae for sine and cosine The distance from P ′ to Q ′ is the square root of Since the line segments PQ and P ′ Q ′ are congruent, then we know that d ( PQ ) 2 = d ( P ′ Q ′ ) 2 . d ( P ′ Q ′ ) 2 = (1 − cos( α − β )) 2 +(sin( α − β )) 2 = 1 − 2 cos( α − β )+cos 2 ( α − β )+sin 2 ( α − β )) = 2 − 2 cos( α − β ) . Smith (SHSU) Elementary Functions 2013 7 / 28 Smith (SHSU) Elementary Functions 2013 8 / 28

Sum and difference formulae for sine and cosine Sum and difference formulae for sine and cosine D 2 = 2 − 2 cos α cos β − 2 sin α sin β In mathematics, if we arrive at the same value through two different computations, we always have valuable information. Here we can equate d ( PQ ) 2 and d ( P ′ Q ′ ) 2 and simplify. Smith (SHSU) Elementary Functions 2013 9 / 28 Smith (SHSU) Elementary Functions 2013 10 / 28 D 2 = 2 − 2 cos( α − β ) 2 Sum and difference formulae for sine and cosine Sum and difference formulae for sine and cosine We create a more memorable form of this equation if we replace β by − β and use the fact that sine is an odd function while cosine is an even function. So 2 − 2 cos α cos β − 2 sin α sin β = 2 − 2 cos( α − β ) 2 . Write cos( α + β ) = cos( α − ( − β )) and replace β by − β in our equation We may divide both sides by 2 and solve for cos( α − β ) . for cos( α − β ) to see that cos( α − β ) = cos α cos β + sin α sin β cos( α + β ) = cos α cos( − β ) + sin α sin( − β ) = cos α cos( β ) − sin α sin( β ) This is an important result. This is an equation we want to record and use on a regular basis. cos( α + β ) = cos α cos β − sin α sin β (1) Smith (SHSU) Elementary Functions 2013 11 / 28 Smith (SHSU) Elementary Functions 2013 12 / 28

Sum and difference formulae for sine and cosine Sum and difference formulae for sine and cosine If we note that sin( θ ) = cos( π 2 − θ ) (since sine and cosine are complementary functions!) then we can write Therefore we have a sum-of-angles equation for the sine function: sin( α + β ) = cos( π 2 − ( α + β )) = cos(( π 2 − α ) − β ) . sin( α + β ) = sin α cos β + cos α sin β (2) Using the sum-of-angles formula above, with regards to the angles π 2 − α If we need, we may replace β by − β to create a difference equation: and β , we have sin( α + β ) = cos(( π sin( α − β ) = sin α cos β − cos α sin β 2 − α ) − β ) = cos( π 2 − α ) cos β + sin( π 2 − α ) sin β = sin α cos β + cos α sin β. Smith (SHSU) Elementary Functions 2013 13 / 28 Smith (SHSU) Elementary Functions 2013 14 / 28 Sum and difference formulae for sine and cosine Sum and difference formulae for sine and cosine I don’t memorize these identities. Here they are again: (That’s one reason I’ve been attracted to mathematics – if one understands the math, one doesn’t need to memorize!) cos( α + β ) = cos α cos β − sin α sin β In the undergraduate classes that I teach at Sam Houston State University, sin( α + β ) = sin α cos β + cos α sin β I will provide students with the sum of angle formulas when they are needed. Smith (SHSU) Elementary Functions 2013 15 / 28 Smith (SHSU) Elementary Functions 2013 16 / 28

Sum and difference formulae for sine and cosine Sum and Difference Formulas Here they are as difference of angles In the next presentation, we will look at some applications of these sum and difference formulas. cos( α − β ) = cos α cos β + sin α sin β (End) sin( α − β ) = sin α cos β − cos α sin β Smith (SHSU) Elementary Functions 2013 17 / 28 Smith (SHSU) Elementary Functions 2013 18 / 28 A reduction formula Let P (cos θ, sin θ ) be a point on the terminal side of angle θ. Any point ( a, b ) on the line ← → OP satisfies the equations a b cos θ = a 2 + b 2 , sin θ = a 2 + b 2 . √ √ Elementary Functions Part 5, Trigonometry Lecture 5.1b, Applications of the Sum and Difference Formulas Dr. Ken W. Smith Sam Houston State University 2013 Smith (SHSU) Elementary Functions 2013 19 / 28 Smith (SHSU) Elementary Functions 2013 20 / 28

A reduction formula Sum and difference formulae for sine and cosine By our sum-of-angles formulas, sin( x + θ ) = sin x cos θ + cos x sin θ. √ a 2 + b 2 sin( x + θ ) . a sin x + b cos x = a b If we replace cos θ and sin θ by a 2 + b 2 and sin θ = a 2 + b 2 , we get √ √ This formula is useful for changing a linear combination of sine and cosine a a 2 + b 2 = a sin x + b cos x b sin( x + θ ) = sin x a 2 + b 2 + cos x . √ √ √ functions into just a sine function. a 2 + b 2 √ √ For example, the function f ( x ) = sin x + 3 cos x can be rewritten as a 2 + b 2 . We clear the denominators by multiplying all sides by √ � a 2 + b 2 sin( x + θ ) . √ √ 2 sin( x + θ ) a sin x + b cos x = (3) 1 2 + sin x + 3 cos x = 3 where θ is the angle between the x -axis and the line from the origin to the √ point (1 , 3) . Since θ = π/ 3 in this problem, and since � √ 2 = √ 1 + 3 = 2 , we have 1 2 + 3 √ sin x + 3 cos x = 2 sin( x + π/ 3) . Smith (SHSU) Elementary Functions 2013 21 / 28 Smith (SHSU) Elementary Functions 2013 22 / 28 Sum and difference formulas for tangent Sum and difference formulae for tangent We know that tan( α + β ) = sin( α + β ) cos( α + β ) so we may use our sum-of-angle tan( α + β ) = tan α + tan β formulas to create a formula for tan( α + β ) . 1 − tan α tan β . A first pass gives tan( α + β ) = sin( α + β ) cos( α + β ) = sin α cos β +cos α sin β cos α cos β − sin α sin β What if we wanted an equation for tan( α − β ) ? But we would really like a sum-of-angles formula for tangent that is in Replace β by − β and use the fact that tangent is an odd function to terms of tan α and tan β. obtain So let’s divide both numerator and denominator by cos α cos β . tan( α + β ) = tan α + tan β tan( α − β ) = tan α − tan β 1 − tan α tan β . (4) 1 + tan α tan β . Smith (SHSU) Elementary Functions 2013 23 / 28 Smith (SHSU) Elementary Functions 2013 24 / 28

Some worked problems Sum and difference formulae for sine and cosine Compute the exact value of cos 75 ◦ . Compute the exact value of sin 15 ◦ . Solution. Solution. Using the sum of angles formula for cosine and the fact that sin 15 ◦ = sin(45 ◦ − 30 ◦ ) = sin 45 ◦ cos 30 ◦ − cos 45 ◦ sin 30 ◦ 75 ◦ = 45 ◦ + 30 ◦ , we have cos 75 ◦ = cos(45 ◦ + 30 ◦ ) = cos 45 ◦ cos 30 ◦ − sin 45 ◦ sin 30 ◦ √ √ √ √ √ 2 3 2 1 6 − 2 = 2 = 2 − 2 2 4 √ √ √ √ √ 2 3 2 1 6 − 2 = 2 = This answer looks familiar! (Notice that since 75 ◦ and 15 ◦ are 2 − 2 2 4 complementary angles so the cosine of one angle is the sine of the other!) Smith (SHSU) Elementary Functions 2013 25 / 28 Smith (SHSU) Elementary Functions 2013 26 / 28 Sum and difference formulae for sine and cosine Sum and Difference Formulas Find the tangent of 75 ◦ . Solution. We could separately compute the sine and cosine of 75 ◦ using our sum-of-angle formulas (as we did on the last slides) or we could use the sum-of-angles formula for tangent and write √ 3 In the next presentation, we will look at double angle and power reduction 1 + tan 75 ◦ = tan(45 ◦ + 30 ◦ ) = tan 45 ◦ + tan 30 ◦ 3 formulas. 1 − tan 30 ◦ tan 45 ◦ = . √ 3 1 − ( 3 )(1) (End) Multiplying numerator and denominator by 3 gives √ tan 75 ◦ = 3 + 3 3 . √ 3 − If we don’t like the square roots in the denominator, we can multiply √ numerator and denominator by 3 + 3 (the conjugate of the denominator) and find that √ √ √ √ tan 75 ◦ = (3 + 3)(3 + 3 3) = (9 + 6 3 3 + 3 ) = (12 + 6 3 √ ) = 2 + 3 . √ √ Smith (SHSU) Elementary Functions 2013 27 / 28 Smith (SHSU) Elementary Functions 2013 28 / 28 9 − 3 6 3 − 3 +